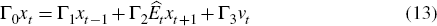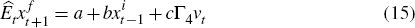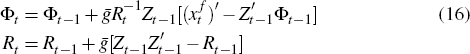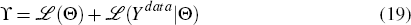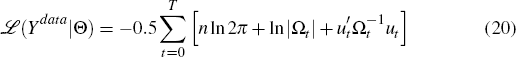RDP 2010-02: Learning in an Estimated Small Open Economy Model 3. Estimating the Small Open Economy Model

We estimate the model using likelihood-based Bayesian methods. This approach has been employed to estimate rational expectations DSGE models in the recent literature.^[7]

3.1 The Law of Motion

Under both rational expectations and learning, the log-linear equations (given in Appendix A) can be summarised by the following system:

where: x_t is a vector of the model variables, a subset (x^f) of which are forward-looking variables (see Equation (A22)); v_t is a vector of exogenous variables (see Equation (A23)); ε_t is a vector of stochastic shocks; and Ê is a possibly non-rational expectations operator. Matrices Γ_j are provided in Appendix A.

If the expectations operator, Ê, was rational we could proceed from here in the usual way and find a solution to the model using standard techniques such as those provided in Sims (2001) and Söderlind (1999). However, when Ê is not rational we need to specify how agents form forecasts of future macroeconomic conditions. That is, we need an expression for 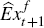(where 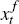is the vector of forward-looking variables in the model: .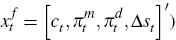

For our learning formulation, we assume that agents know the structure of the economy (as embodied in Equations (A1)–(A16)) but are unsure of its parameters and how shocks propagate (that is, they do not know a, b or c below). We assume that agents update their beliefs about forward-looking variables according to:^[8]

where: xⁱ is a subset of model variables that are used to estimate x^f ; and matrices a, b and c denote agents' time-varying estimates of the model's reduced form. Note that the learning rule in Equation (15) assumes that agents observe current values of exogenous variables (that is, they know v_t). This is a common simplifying assumption made in learning models. However, we assume that private agents begin period t with estimates a, b and c based on data through t−1. That is, they know 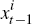. At t+1 agents add the new data point 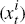to their information set to update their estimates of a, b and c using recursive least squares, for instance.

We consider two slightly different learning rules. One, which we describe as Minimum State Variable learning (MSV), is more restrictive and is used as a robustness check (see Section 4.3 and Appendix C for a discussion of these results). Under this approach, agents include in 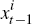only those variables which do not ‘jump’ (that is, those variables that correspond to non-zero columns in Γ₁). This learning rule is closely associated with the rational expectations version of the model.^[9] So, under this approach, a lagged value of the nominal exchange rate is not used as an explanatory variable in xⁱ, even though a one-step-ahead forecast of it is formed.

The other learning rule relaxes this information assumption slightly and is used as our benchmark. We label this learning rule as ‘VAR learning’ since agents incorporate lagged values of all variables that are forecasted in x^f, including the lagged value of the exchange rate.

There are many choices of algorithms to estimate the parameter matrix 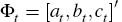. Constant-gain learning is the standard algorithm used to model learning in empirical macroeconomics. This places more weight on recent information, which helps the model handle structural change.^[10] The constant-gain learning rule is

where: ḡ is the gain parameter; 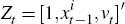denotes data of the current period; Φ_t denotes the coefficient estimates; and R_t is the matrix of second moments of Z_t. Each period, agents adjust their estimates from the last period by a fraction ḡ of the weighted difference between the realised 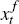and the forecast made last period 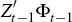. We follow Milani's (2007) approach and jointly estimate the gain parameter with the structural parameters.

Taking Equation (15) one step ahead gives the general form of the forecasting equation. This can be substituted into Equation (13) to get the implied ‘Actual Law of Motion’ (ALM) for the learning model:

where .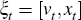

The ALM for both the learning model and the rational expectations model are mapped to the data using the measurement equation

where: 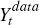contains the observable time seri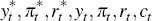es and Δq_t (the data are described in detail in Section 3.3); the matrix H maps the variables in the state vector (ξ_t) to the observed data; and e_t is measurement error specified as white noise. We allow for measurement error in all observable variables.

3.2 Forming the Posterior

The log posterior distribution of the parameters to be estimated (Θ) is given by

where ℒ(Θ) is the logarithm of the prior probability of the parameters Θ and ℒ(Y^data|Θ) is the log likelihood of observing Y^data given the parameters Θ. Details of the prior probabilities are provided in Section 3.3.

The likelihood is given by

where: n is the number of observable variables; Ω_t is the covariance matrix of the theoretical one-step-ahead forecast errors implied by a given parameterisation of the model; and u_t is a vector of the actual one-step-ahead forecast errors from predicting the variables in the sample Y^data using the model parameterised by Θ. The likelihood is computed using the Kalman filter.

The mode of the posterior distribution is found by numerically optimising Equation (19) using Bill Goffe's simulated annealing algorithm. The posterior distribution is found using a Random-Walk Metropolis-Hastings algorithm using 2 million draws (with a 25 per cent burn-in period).

3.3 Data Description and Priors

The model is estimated using data from 1993:Q1 to 2007:Q1. For the domestic variables we use: (linearly detrended) real non-farm GDP, the (demeaned) cash rate, (demeaned) CPI inflation, the (demeaned) real exchange rate appreciation and (linearly detrended) real household consumption. Linearly detrended trade-weighted G7 real GDP is used as data for foreign real GDP. Demeaned data for the foreign nominal interest rate and inflation are simple averages of US, euro area and Japanese interest rates and inflation series respectively. Details of the data used can be found in Appendix B.

The priors, which are chosen to conform with the constraints implied by theory, are described in the first three columns of Table 1. We fix the household discount rate β equal to 0.99 and the share of imports α equal to 0.18. Fairly loose gamma priors are imposed on the elasticity of labour supply (γ) and the intertemporal elasticity of substitution (φ). The price stickiness parameters (θ^d, θ^m) are assigned beta priors that are based on the mean quarterly duration found in Australian data (see Jääskelä and Nimark 2008) with a mean of 0.6 and a standard deviation of 0.05. The priors for the structural shocks (σ) are inverse gamma distributions with a mean of 0.001 and a standard deviation of 0.02, reflecting the fact that there is little prior information on the shocks. The sensitivity of our results to alternative priors is analysed in Section 4.3.

Footnotes

An and Schorfheide (2007) and Smets and Wouters (2003), for example. [7]

In the learning literature, Equation (15) is known as the Perceived Law of Motion (PLM) of the agents. [8]

This is often referred as the MSV solution, however, we also include a constant term a in agents' perceived law of motion, which implies that agents do not know the steady-state values of the economy. [9]

Evans and Honkapohja (2001) show that under certain conditions the constant-gain learning equilibrium will converge to a distribution around the rational expectations equilibrium. [10]