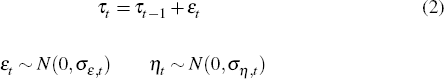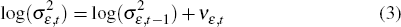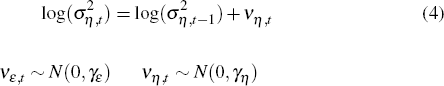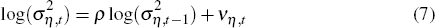RDP 2009-06: Inflation Volatility and Forecast Accuracy 2. Methodology and Data
October 2009
Our benchmark model follows Stock and Watson (2007), who characterise the inflation process with an unobserved component model with stochastic volatility (UC-SV). In this model, inflation (πt) is expressed as the sum of a permanent stochastic component (τt)and a transitory innovation component (ηt) as per Equation (1). The permanent component of inflation evolves as a random walk without drift as in Equation (2).[4] The variance of the shocks (εt) to this component can change over time, as can the variance of the transitory innovations.
The relative importance of τ and η is determined by their variances (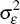
and 
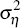), which evolve as
independent random walks (without drift). The only parameters of the model
are γε
and γη, which are the standard deviations of
νε and νη. They
control the speed at which the size of the permanent and transitory shocks
can change. If all the νi,t shocks were zero after
date t0, then the variances 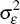and 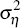would stay fixed at
their date t0 values, and the model would simply become
a random walk observed with noise, as in Equations (1) and (2).
Using Equations (1) to (4), we can estimate the evolution of τt,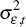 
and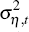 
, conditional on inflation
data
(πt).[5]
It is possible to set the values of γε and
γη by calibration – Stock and Watson (2007,
2008) use this approach – but we chose to estimate them, and thereby
allow for cross-country variation in our analysis.
2.1 A Modification of the Stock and Watson Model
This section describes a modified version of the UC-SV model (M-UC-SV), which in principle should be preferred when looking at questions related to forecasts. While the model of Stock and Watson (2007, 2008) provides a useful way to assess the within-sample properties of the inflation process, it is less satisfactory for questions related to forecastability. In particular, their model implies that inflation has a unit root and the variances of the permanent and the transitory components are unbounded, so the model becomes explosive over longer horizons (Pagan 2008; Bos, Koopman and Ooms 2007).[6]
The M-UC-SV model relaxes the assumption that the permanent component of inflation is a random walk, and assumes instead that there are persistent shocks around a fixed mean (μ):
where ϕ is constrained to be less than one in absolute value. This constraint rules out an explosive root in inflation.
We also allow univariate stochastic volatility processes to evolve as auto-regressive processes:
This assumption forces the variances of the persistent (εt) and temporary (ηt)
components of inflation to be bounded; we estimate μ and ϕ
using the Gibbs sampler, but calibrate ρ to
0.98.[7]
In this model, if the νi,t shocks were set to zero
after period t0, then the logs of 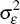and 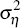would converge to
zero, meaning that their levels would approach one, so that the ε
and η shocks in Equations (7) and (8) would become standard normals.
Our focus will be on the time-varying volatilities 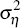and .
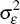For completeness, Tables C1, C2 and C3 in Appendix C
provide estimates of μ, ϕ, γε
and γη for the countries in our sample.
2.2 Data
We use CPI series that are corrected (where possible) for changes to indirect taxation (and the direct effects associated with changes in interest rates).[8] In some cases it is not possible to correct inflation for the effects of movements in indirect taxes. We provide more details in Appendix A. For the United Kingdom we used the retail price index excluding mortgage interest (RPIX).
Where possible, we use data commencing in 1960. As described in Appendix A, we used seasonally adjusted quarterly data. Some countries publish seasonally adjusted CPI series; for the remainder, we used X-12-ARIMA to remove the seasonal component.[9]
Footnotes
See also Cogley and Sargent (2001, 2005), Ireland (2007), and Cogley and Sbordone (2008) for papers that model trend inflation in this way. [4]
To do this we apply the Gibbs sampler. [5]
If the model is used to simulate 50 years' worth of data, starting from initial values calibrated for the United States, at least one hyperinflation is very likely. [6]
We tried including a freely-estimated mean and AR(1) coefficient in Equations (7) and (8), but the Gibbs sampler became numerically unstable. Models with calibrated values of ρ between 0.9 and 0.99 are hard to distinguish; lower calibrated values produce slightly worse forecasting performance, and are not as stable numerically. [7]
We also performed the analysis using central bank ‘preferred’ measures of inflation (where applicable), such as the personal consumption expenditure deflator for the United States. In general, the results are broadly similar to those presented below. [8]
Monthly data were seasonally adjusted if needed and then converted to quarterly data by taking averages of the monthly observations. [9]