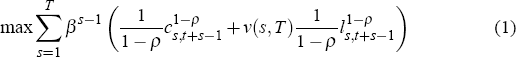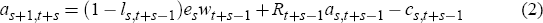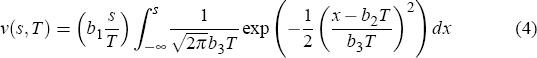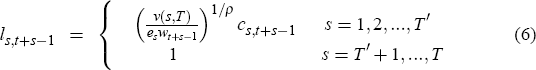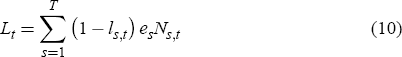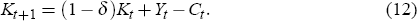RDP 2006-06: Ageing, Retirement and Savings: A General Equilibrium Analysis 3. The Model

At any point in time, the economy is populated by a finite number of generations and a representative profit-maximising firm. Every period the oldest generation dies and one new generation enters the economy. Households live for T periods, choose to work for T′ ≤ T, consume, and supply capital and labour to competitive factor markets. Agents have perfect foresight and there is no government or foreign sector.

3.1 Households

Individuals within a generation are equal in every respect. Agents start and end life with no wealth, as there are no bequests and no uncertainty about the time of death. Formally, an agent born at time t maximises lifetime utility

by choosing sequences of consumption and leisure, 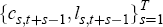subject to a period budget constraint of the form

and period inequality constraints on leisure of the form

as well as initial and terminal conditions on individual wealth.^[9] In the equations above: c_s,t is time t consumption of an agent s years old; α_s,t is the beginning of period t stock of wealth of an agent s years old; R_t = 1 + r_t − δ is the rate of return to capital between t and t + 1, where δ ∈ (0,1) is the depreciation rate of the capital stock between t and t + 1; e_s is an age-specific constant that captures differences in human capital or productivity across cohorts; β ∈ (0,1) is the household's subjective discount factor; and the parameter ρ > 0 governs the degree of inter- and intra-temporal substitution.

As in Bloom et al (2004), the disutility of working depends on an individual's health status, which in turn is negatively related to age and is captured in the function ν(s, T). Consistent with the weight of evidence on this issue (Sickles and Taubman 1986; Fogel 1994, 1997; Costa 1998; Mestdagh and Lambrecht 2003; Cai and Kalb 2004), we assume that increases in life expectancy are associated with improved health status. In particular we assume that the function is given by

where the parameters b₁, b₂, and b₃ are strictly positive. The function ν is the cumulative distribution function of a normal random variable with mean b₂T and standard deviation b₃T, scaled by 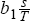. We chose this specification for a number of reasons. First, v is an increasing function of age, s, and a decreasing function of life expectancy, T. Therefore as the individual ages, the function magnifies the disutility from work that arises because of deteriorating health. Second, ν is homogeneous of degree zero in s and T.^[10] This has the important implication that the disutility from work does not depend on absolute age, but rather on an agent's age relative to their lifespan. In other words, the disutility from work of an agent 40 years old with a lifespan of 60 years is equivalent to that of an individual 60 years old with a lifespan of 90 years.^[11] Finally, we can choose the mean and standard deviation in ν (b₂T and b₃T') so that agents' labour supply decisions match observed age-specific participation rates.

For an individual that works for the first T′ periods, the Kuhn-Tucker first-order conditions yield a solution of the form

where an expression for initial consumption (c_1,t) can be found in Appendix A. Equation (5) is the Euler equation for consumption. It shows that when the interest rate is equal to the inverse of the discount factor, the consumer desires a flat lifetime consumption path. An even higher rate of interest would give rise to an upward-sloping consumption profile. At a utility maximum, the consumer is unable to gain from feasible shifts of consumption between periods. A one-unit reduction in present consumption lowers lifeti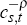me utility by , the marginal utility of present consumption. This saved consumption unit can be converted into R_t units of consumption in the following period, raising lifetime utility by 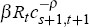. Equation (5) states that at an optimum the agent equates these quantities.

It is worth emphasising that, unlike many OLG models, T′′ is not exogenous but must be determined by the individual as part of the solution. The smooth nature of v allows us to focus on cases where the agent works initially and retires later on because paths for leisure that would imply expected reversals of retirement would not be optimal. However, some agents might reverse their retirement decisions in the presence of unanticipated changes in parameters such as T and e_s. For example, in the presence of an unanticipated rise in life expectancy, a retired agent might rejoin the workforce to avoid a drastic decline in consumption over their (now longer) life. Indeed, situations such as this occur in the simulations below.

Equation (6) shows that, other things equal, a reduction in the disutility from work, ν(s,T), induces the individual to demand less leisure and favour a later retirement. In general equilibrium, there are second-round effects because the change in ν(s, T′) affects aggregate labour supply and puts downward pressure on wages. Depending on the relative strength of the income and substitution effects, this might offset some of the move towards later retirement, as the incentives to work are now lower. Equation (6) also shows that, even if there are no changes in individual preferences caused by changes in T, factors that alter the path of wages and interest rates – such as a baby boom or technological change – could also change retirement decisions.

3.2 Firms

There is a single competitive production sector using capital and labour as inputs into a Cobb-Douglas production function with constant returns to scale

where Y_t,K_t, and L_t are the aggregate levels of output, capital and efficient labour at time t, and α ∈ (0,1). The variable A captures total factor productivity and is to some degree a scaling constant. However, for a given profile of human capital, e_s, increases in A have real effects that go beyond mere changes in the unit of account. As in Auerbach and Kotlikoff (1987), the model lacks a well-defined steady state when A grows at a constant rate over time.^[12]

As a result of profit maximisation we obtain the standard factor-demand curves which can be written in intensive form as

where k_t = K_t/L_t is capital per efficient worker.

3.3 Aggregation and Equilibrium

If N_s,t denotes the number of individuals s years old that are alive in period t, then the total population, N_t, is simply 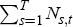. The effective work force at time t is

We assume that cohorts grow at a constant rate n governed by the law of motion N_s,t = (1 + n)N_s,t−1.^[13] As this growth rate n determines the relative size of the different cohorts, we interpret it as a fertility parameter. In steady state, where T and n are constant, the rates of cohort and population growth will be identical, and the total population would evolve according to N_t = (1 + n)N_t−1.

In equilibrium, the supply of capital (the aggregate wealth of agents in period t) must be equal to the capital stock that firms demand at t.

The dynamics of the economy are governed by the evolution of the aggregate stock of capital. Combining the capital accumulation constraint with the resource constraint of the economy, we obtain the equilibrium law of motion of the economy

Footnotes

The agent is born with no wealth (α_1,t = 0), and dies with no wealth (α_T+1,t+T = 0). [9]

One way to ensure that a function is homogeneous of degree zero is if it is the product of two functions that both have this property. In the case of v, it is easy to see that the term 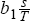is homogeneous of degree zero in s and T. The other term, the cumulative distribution function of a normal random variable, also has this property. This can be seen by considering that every cumulative normal distribution evaluates to ½ at its mean, and contains the same amount of probability within any given number of standard deviations as any other cumulative normal distribution. Changing the values of s and T by the same proportion would result in the same number of standard deviations as at their original values, and thus the same value of the cumulative density function, which implies homogeneity of degree zero as required. [10]

Bloom et al (2004) use the function v(s,T) = aexp(s/T), and assume that the agent chooses an indicator variable that takes the value of one when working and zero when retired. In this way, the agent either works full-time or retires. The problem of directly attaching a function of this form and not using an indicator variable is that labour elasticities would vary unrealistically with age. [11]

If A grows over time, wages will grow over time and the consumption-leisure ratio will trend towards ever-increasing or ever-decreasing labour force participation. Auerbach and Kotlikoff argue that, in the long run, an ever-increasing A would lead to an absurd result. While the technical issue about an ever-increasing A cannot be ignored in our model, we would like to emphasise that the model implies that technical improvements reduce the age of retirement. This is important because, even though life expectancy has been growing in most countries, the effective age of retirement has fallen or stayed constant in a number of them. [12]

Alternatively we could write N_s,t = (1+ n)N_s+1,t by noticing that N_s,t−1 = N_s+1,t. [13]