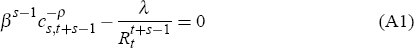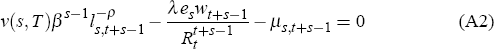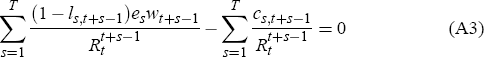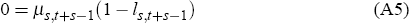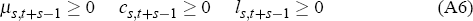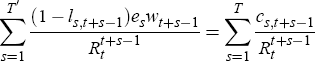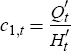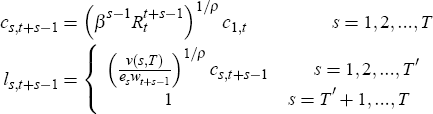RDP 2006-06: Ageing, Retirement and Savings: A General Equilibrium Analysis Appendix A: Technical Appendix

A.1 The Household Problem

The household problem is to maximise Equation (1) subject to the period budget constraint, Equation (2), inequality constraints on leisure given by Equation (3), initial and terminal conditions on individual wealth (a_1,t = a_T+1,t+T = 0), and non-negativity constraints on consumption and leisure.

Let λ and µ_s,t+s−1 be the Lagrange multipliers associated with the lifetime budget constraint and the period t + s − 1 inequality constraint on leisure, respectively. With a priori knowledge about the functional form of ν(s, T) we can infer that c_s,t+s−1 > 0 and l_s,t+s−1 > 0. Lifetime resources would be exhausted along the optimal path, so the lifetime budget constraint would be active. With this in mind, the Kuhn-Tucker first-order conditions of the problem can be written as

Where .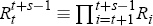

There are three main cases to consider with respect to the solution. One in which the constraint on leisure, Equation (A4), never binds; one in which Equation (A4) is always active; and one in which Equation (A4) is initially not active, but becomes active later on. The first case lies at the interior of the opportunity set and poses no difficulty. It is easy to show that the second case is not optimal if initial and terminal wealth are zero. In this case, the agent can never consume as no income is ever generated. So we can rule out the first and second case and concentrate on the third in which the agent works a given number of periods and retires from then on.

Assume that Equation (A4) is not active for s = 1, ...,T′ and is active for s = T′ + 1, ...,T. In this case, the plan for consumption and leisure implicitly incorporates the time of retirement. One can view the agent as choosing the cutoff period, T′, after which the constraint ceases to be inactive. In this case we can rewrite the lifetime constraint as follows

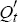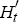Define the variables and as

The first-order conditions of the problem can be combined with the lifetime budget constraint and the above definitions to arrive at an expression for the household's first-period consumption of the form

with an expression for c_1,t the optimal path for consumption and leisure satisfies Equations (5) and (6)

Note that this is not a closed form analytical solution for c_s,t and l_s,t because T′ is not a fixed parameter of the household's problem but, rather, a choice variable.

Formally, T′ never enters the problem or forms part of the solution. Rather, it is a convenient indicator of when the Lagrange multipliers associated with the leisure constraints are zero, and allows us to express the solution without reference to the Lagrange multipliers.

Although analytical expressions are not available in the case of OLG models of large dimensions, the problem can be solved numerically. The next section discusses the solution method.

A.2 The Solution Method

Solving for the steady state of the model involves solving a system of non-linear equations and inequality constraints. We solve for the equilibrium of the economy in the initial steady state using Gauss-Seidel iterations.^[26] With respect to T′ we use an initially constrained approach, as described in Intriligator (1971), in that our initial guess of the leisure profile is inside the agent's opportunity set. Our initial guess is that the agent does not retire (i.e., T′ = T, which implies l_s,t+s−1 < 1 for all s).

The algorithm for solving the steady state is illustrated in Figure A1. We start with an initial guess of the aggregate capital stock and labour supply. With these values in hand we calculate factor prices. We then use our initial guess of T′ to calculate leisure and consumption sequences. The leisure sequence gives us a new guess for T′. If this new guess is not equal to our initial one, we update our guess of T′ and recalculate leisure and consumption sequences. Otherwise, we update labour supply and get a new value for the capital-to-labour ratio and factor prices. Once labour supply converges, we calculate individual wealth and aggregate it to get a new guess of the aggregate capital stock. A fixed point of this algorithm yields the steady-state capital-to-labour ratio.

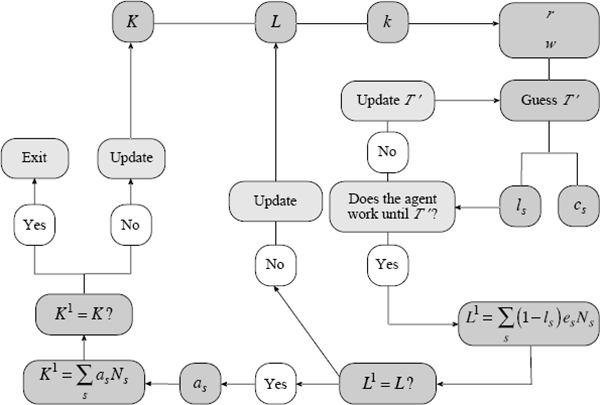
To solve for the equilibrium transition path we use a strategy similar to Auerbach and Kotlikoff (1987). Finding the transition path is conceptually like finding the steady state. Some additional complications are worth mentioning. As the economy undergoes a transition in which conditions change over time, it is necessary to solve explicitly for each year. And because agents are forward-looking, it is necessary to solve for equilibrium in all transition periods simultaneously. In our simulations we generally give the economy around 250 years to adjust to the final steady state. After 250 years, we constrain the economy to attain its final steady state. The idea is to allow the economy to settle down by itself well before 250 years.^[27]

Agents that are alive at the time of the change need to be treated differently. At the time of the change they are ‘reborn’ with an ‘initial’ wealth equal to whatever they had accumulated up to that point, and a ‘shorter’ lifespan equal to T minus what they had already lived. One appealing property of any steady state in the model is that it can be interpreted both in its cross-sectional dimension or in its time dimension. For example, the steady-state leisure profile can be seen as the time t leisure that each agent of age s takes, or as the leisure profile that an individual born at t can expect to have if conditions do not change throughout their life. A complication of the transition path is that, since conditions are changing over time, individuals born at different times might choose different retirement ages.

It is necessary to keep track of every single generation's age of retirement, which implies that a single guess for the age of retirement (T′ + 1) is not sufficient. In other words, it could well happen that at some time t all agents alive might choose different retirement ages.

In cases where we are modelling a baby boom followed from a baby bust there is an initial set of parameters, an intermediate one, and a final one. It is therefore necessary to calculate a transition path which would never occur, but which influences expectations of future prices. People behave as if the intermediate steady state would last forever, and are surprised later on with a new set of changes. In this case, it is necessary to calculate a virtual transition path, and use the conditions on that path as the initial conditions when the second change occurs.

Footnotes

Matlab programs for the steady state and transition paths are available upon request. [26]

In particular, with experiments that involve increases in T it is necessary to make sure that the economy has sufficient time to adjust. This is because, the larger the value of T, the longer the economy takes to arrive at the new steady state. Numerical simulations suggest that the time the economy needs to converge grows proportionately more than T. [27]