RDP 2005-04: Monetary Policy, Asset-Price Bubbles and the Zero Lower Bound 4. Results

In this section we present the optimal policy recommendations of activist and sceptical policy-makers, through time, in the presence of an asset-price bubble. As noted in Section 2, we focus on the period while the bubble survives and grows. Once the bubble bursts, both activists and sceptics in our Ball-Svensson model will always agree on an approach of aggressively easing policy to counteract the contractionary effects of the bust.

As in Gruen et al (2003), we wish to examine the optimal policy recommendations of sceptics and activists over a range of alternative assumptions about the stochastic nature of the bubble. To do so meaningfully, it is necessary that the two policy-makers face an economy in the same state in each year. Since the current state of the economy depends on previous policy settings (as well as on the evolution of the bubble) we will assume throughout that the policy settings which are actually implemented each year are those chosen by the sceptic. We can then sensibly compare, as each year passes, the current optimal policy recommendations made by the different policy-makers.

The activist's recommendations will depend on the assumptions he makes about the future possible paths of the bubble. In particular, they will reflect the economic effects implicit in these paths, and how these effects interact with both his preferences, as reflected in his loss function, Equation (11), and the potential constraint on his future actions embodied in the ZLB. By contrast, as a believer in the efficient markets hypothesis, the recommendations of the sceptic will reflect an expectation of no future effects on the economy flowing from asset-price movements.

4.1 Baseline Results: the Case of Exogenous Bubbles

We begin with results for the baseline case where: the bubble's future development is unaffected by policy-makers' actions; its direct expansionary effect on output in each year of its growth is a constant 1 percentage point (γ_t = 1); its period-to-period probability of bursting is a constant 40 per cent (p_t = p* = 0.4); and the model and loss function parameters α, β, λ and μ take their baseline values (namely α = 0.4, β = 1.0, λ = 0.8 and μ = 1.0) specified earlier.^[7] In subsequent subsections we will examine the effect of varying each of these sets of assumptions.

Figure 2 shows the optimal policy recommendations made in each period by the sceptic and two activists, assuming that the steady-state neutral nominal interest rate in the economy is i* = 3 per cent.^[8] The two activists differ in the way that their actions are influenced by the ZLB. For the first, the ZLB is a genuine constraint on policy, as encapsulated by Equation (6). For the (hypothetical) second, the ZLB is not a constraint, so that a negative nominal interest rate setting can (in some unspecified way) be achieved, if desired.

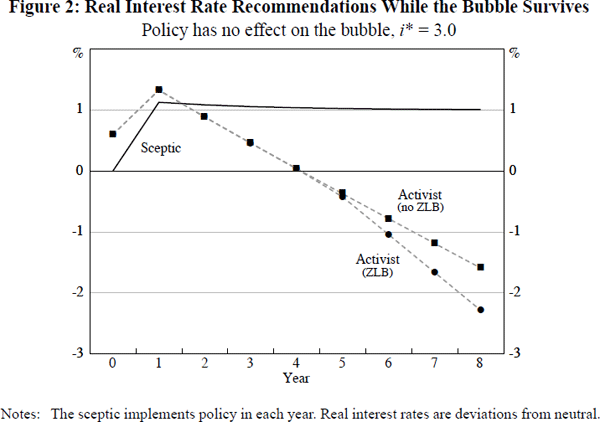
The most striking feature of Figure 2 is that the recommendations of an activist (whether affected by the ZLB or not) are initially above those of the sceptic, but subsequently drop below them. This reflects that an activist is chiefly concerned, in the early stages of the bubble, with the expansionary impulse that it will impart to the economy next period, if it survives. By the time that the bubble has reached even a moderate size, however, this concern begins to be outweighed by the risk that the bubble may burst next period, causing a significant negative shock to the economy. Due to the lags with which policy affects the economy, activist policy-makers become anxious not to risk compounding such a shock next period, should the bubble burst, through an overly tight policy recommendation this period. For a detailed discussion of the differences between the policy recommendations of a sceptic and a ‘no ZLB’ activist, across a range of alternative assumptions about the bubble process and its responsiveness to policy, we refer the reader to Gruen et al (2003).

Our focus in this paper, however, is on the difference between the two sets of activist policy recommendations shown in Figure 2. This difference captures the impact of the presence of the ZLB on an activist policy-maker's preferred recommendations. Two characteristics of this difference stand out. First, as anticipated in Section 3, for an exogenous bubble the effect of the ZLB is indeed to make an activist reduce his interest rate recommendations in each period, at the margin, relative to what he would have recommended were there no ZLB. Secondly, even for an economy with a low steady-state neutral nominal interest rate of i* = 3 per cent, this effect is, however, very small at first: it is not until year 6, for example, that an activist in such an economy would feel the need to lower his policy recommendation by even 25 basis points on account of concern about the ZLB.

We can explore these latter two observations further by considering how the impact of the ZLB on an activist policy-maker varies with the level of the steady-state neutral nominal interest rate in the economy, i*. Figure 3 shows the difference between the policy recommendations of activist policy-makers, with and without a ZLB constraint, for i* = 1, 2, 3, 5.5 and 8 per cent. The choice of i* = 5.5 per cent is covered to include a case in the plausible range of values for Australia: corresponding to, say, a neutral real interest rate of 3 per cent and an inflation target of 2.5 per cent, the midpoint of the 2–3 per cent medium-term target band. As discussed by Stevens (2004), an examination of Australia's economic performance since the early 1990s might suggest that this figure lies around the middle of the range of possible values for Australia's current neutral nominal interest rate. The choices i* = 1 and 2 per cent are included to show the increasingly severe impact of the ZLB on an activist policy-maker's considerations when the neutral nominal rate is extremely low.

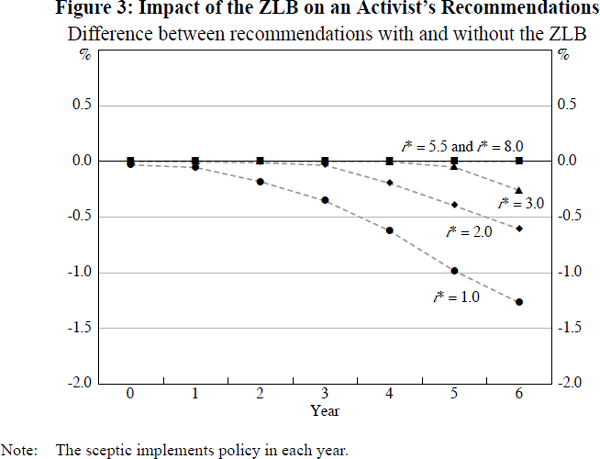
We see that for neutral nominal interest rates around or above the likely current level for Australia, the ZLB is not a factor in an activist policy-maker's thinking, even for quite large bubbles. By contrast, in an economy with an extremely low steady-state neutral nominal interest rate, such as i* = 1 or 2, the ZLB would start to become a serious factor in an activist policy-maker's considerations even for small to moderate sized bubbles.

We now examine how these observations vary across a range of alternative assumptions about the stochastic properties of our asset-price bubbles, and about the model parameters α, β and λ.^[9]

4.2 Exogenous Bubbles with Different Probabilities of Bursting

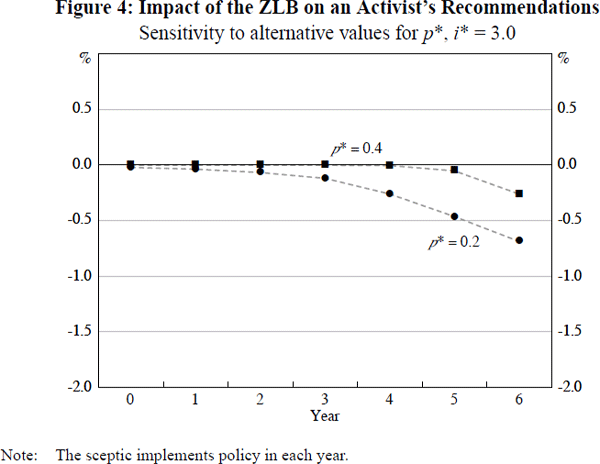
The results in Figure 2 suggest that, for an exogenous bubble with period-to-period probability of bursting p_t = p* = 0.4, the ZLB is not a major factor in an activist policy-maker's considerations, unless the steady-state neutral nominal interest rate in the economy is extremely low. It is interesting to ask whether this remains so as we vary the constant probability of bursting, p*.

For small values of p*, the probability that the bubble will continue to grow to a large size, rather than burst in the near term, increases. We would therefore expect that, the smaller the value of p*, the greater would be the importance of the ZLB in an activist policy-maker's thinking as a possible constraint on future action.

As Figure 4 shows, this is indeed what we find. For an exogenous bubble whose period-to-period probability of bursting is p_t = p* = 0.2, the impact of the ZLB on an activist's recommendations is apparent both earlier and more forcefully than in the case where p_t = p* = 0.4: in the former case the ‘ZLB effect’ is around 25 basis points by year 4, and 50 basis points by year 5, whereas in the latter case it is not until year 6 that it even reaches 25 basis points.^[10] Nevertheless, the scale of this ‘ZLB effect’ is not very large in either case, nor is it dramatically different between the two cases, at least until the bubble has become quite large.

4.3 Bubbles Whose Growth is Affected by Policy

In Sections 4.1 and 4.2 we considered only purely exogenous asset-price bubbles. A natural extension is to assume that, by setting tighter policy this year, policy-makers can reduce the extent of the bubble's growth next year, if it survives. Explicitly, we assume once again that p_t = p* = 0.4 (except p₁₄ = 1), but that now, following Gruen et al (2003),

where: 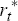, t ≥ 0 denotes the optimal path chosen by a sceptical policy-maker while the bubble survives, assuming γ_t = 1; and ϕ is a sensitivity parameter to be chosen.^[11] For the case ϕ = 1, setting policy 1 percentage point higher than the sceptic this year thus means that the bubble's growth next year would be reduced from 1 per cent to nothing.^[12]

In this setting, and for an economy with i* = 3, Figure 5 shows a comparison of the optimal interest rate recommendations of a sceptic and three activists, while the bubble survives. Two of these activists differ in their assumptions about the sensitivity parameter ϕ, with one assuming no interest-rate sensitivity, ϕ = 0, while the other assumes high sensitivity, ϕ = 1. The third, for reference, is a hypothetical policy-maker who also assumes high sensitivity (ϕ = 1), but is unconstrained by the ZLB.

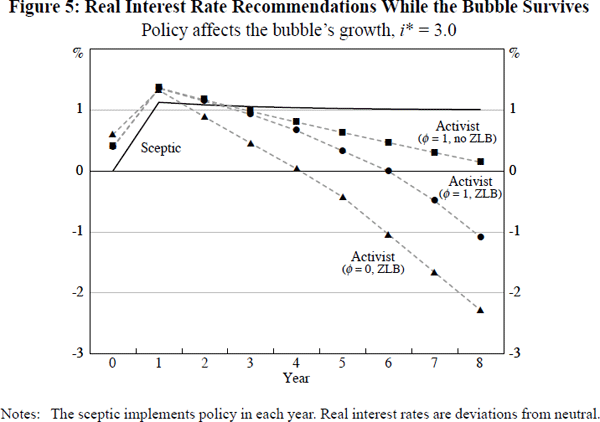
As discussed in Gruen et al (2003), being able to influence the growth of the bubble makes an activist policy-maker increase their policy recommendations in each period from year 1 onwards, relative to the case of an exogenous bubble. However, the impact of the ZLB is still to reduce such an activist's policy recommendations, relative to what they would prefer in the absence of the ZLB. Moreover, this ‘ZLB effect’ now manifests itself both earlier and more strongly than in the previous setting of an exogenous bubble.^[13]

We can interpret these latter results in terms of the ‘insurance framework’ for analysing the impact of the ZLB, described in Section 3. Recall that, for bubbles whose growth is affected by policy, two alternative forms of insurance against encountering the ZLB are available to an activist policy-maker: building a buffer of inflation and output against the effects of the bubble's eventual collapse, by running policy more loosely than otherwise; or holding down the size of the bubble, and hence the size of the negative shock it will impart upon bursting, by running policy more tightly than otherwise.

The fact that the ‘ZLB effect’ in Figure 5 is again downwards shows first of all that, for a Ball-Svensson economy with our baseline parameters and a neutral nominal interest rate of i* = 3, the former type of insurance must be more cost-effective than the latter for a bubble whose growth can be influenced by policy (according to Equation (16) with ϕ = 1). As for the observation that this ‘ZLB effect’ is now evident both earlier and more strongly than for an exogenous bubble, this reflects the presence of two added feedbacks in this setting relative to the exogenous bubble case – between an activist's recommendations on the one hand, and the structure of Equation (16) on the other.

In more detail, suppose that, in the current setting, an activist is contemplating recommending looser policy than otherwise, on account of the future risks arising from the ZLB (as Figure 5 shows he will do). For each basis point by which he does so, he is aware that this will now have the effect of increasing the expected growth of the bubble next period, if it survives, by an equal amount. This will have two competing effects. On the one hand it will partially offset the decrease in these future risks which he would hope to achieve through the loosening of policy, and so require him to recommend policy be moved further to achieve his optimal level of insurance than he would in the exogenous bubble case. On the other hand it will provide him with a greater cushion of output and (future) inflation than otherwise, and so reduce the extent of loosening he may feel is required. The results in Figure 5, which show the magnitude of the ‘ZLB effect’ to be larger in each period than in the exogenous bubble case (Figure 2), suggest that it is the former feedback which dominates in the current setting.

Once again, it is interesting to consider the sensitivity of these results to changes in the assumed steady-state neutral nominal interest rate of the economy. This is illustrated in Figure 6, which shows the difference between the policy recommendations of activist policy-makers, with and without a ZLB constraint, for i* = 1, 3 and 8 per cent. Here, these activists assume again that policy can affect the bubble's growth according to Equation (16) with ϕ = 1.

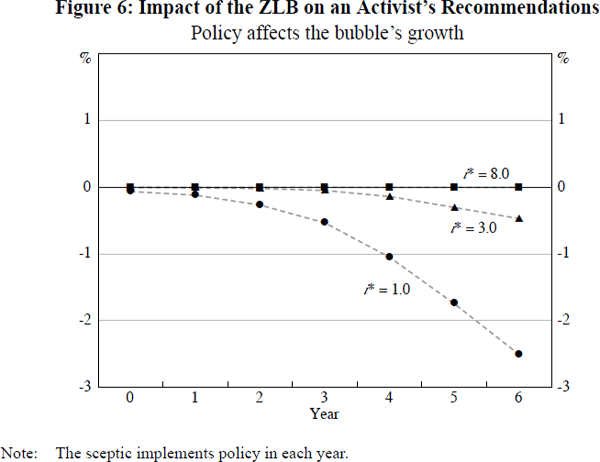
We see that, for our baseline Ball-Svensson model, the compounding effect just described becomes yet more acute if i* is extremely low, so that for i* = 1 per cent the downward ‘ZLB effect’ on an activist's recommendations is already noticeable by year 2, and exceeds 1 percentage point by year 4. By contrast, this ‘ZLB effect’ is still negligible, even in year 6, if i* is set to be 8 per cent, well away from zero.

4.4 Bubbles Whose Probability of Bursting is Affected by Policy

Next, instead of a bubble whose growth is affected by policy, consider a bubble whose period-to-period probability of bursting may be influenced by the actions of policy-makers. Specifically, assume that, by setting tighter (looser) policy this year, policy-makers can raise (lower) the probability that the bubble will burst next year, according to the relationship

where: 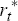, t ≥ 0, denotes the optimal path chosen by a sceptical policy-maker while the bubble survives; and where b = ln((1 − p*)/p*) and a = −δ/(p*(1 – p*)) for some constant p* and some fixed sensitivity parameter δ.

We choose this functional form, which was also used in Gruen et al (2003), for three reasons. First, it ensures that, while raising last year's interest rate, r_t–1, raises the probability that the bubble will burst this year, p_t, it cannot drive this probability to one. Secondly, it possesses the property that p_t = p* when 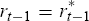, the benchmark policy settings chosen by the sceptic. 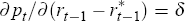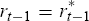Finally, it has the property that when this derivative is evaluated at , so that the parameter δ gives the marginal sensitivity of the bubble's probability of bursting to changes in the real interest rate, at the sceptic's benchmark settings. For the results which follow we adopt the baseline choices p* = 0.4 (except p₁₄ = 1), consistent with the bulk of our earlier simulations, and δ = 0.2, corresponding to a moderate level of interest rate sensitivity. In this setting, and for an economy with i* = 3, Figure 7 shows a comparison of the optimal interest rate recommendations of a sceptic and two activists, while the bubble survives. The two activists differ in the way that their actions are influenced by the ZLB: the first is constrained by it while the second is not.

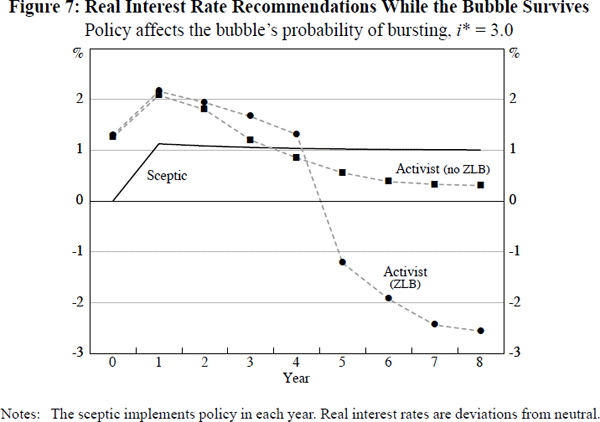
The most striking feature of Figure 7 is that the impact of the ZLB is no longer in a uniform direction over time. Up to and including year 4, the effect of the ZLB on an activist policy-maker is to make them recommend tighter policy than otherwise. However, in year 5 this shifts, and the effect of the ZLB becomes such as to cause an activist to recommend looser policy than otherwise, in this and subsequent years. Moreover, this shift is quite dramatic, with the ‘ZLB effect’ on an activist policy-maker moving from positive 46 basis points in year 4 to negative 178 basis points in year 5.

Once again, we can interpret these results in terms of our ‘insurance framework’ from Section 3. Recall that, as for bubbles whose growth is affected by policy, in the current setting there are two alternative forms of insurance against encountering the ZLB available to an activist policy-maker. The first is the standard approach of building a buffer of extra inflation and output against the effects of the bubble's eventual collapse, by running policy more loosely than otherwise. The second is to seek to burst the bubble before it can grow further, and so become a bigger threat to economic stability whenever it does collapse, by running policy more tightly than otherwise.

The results in Figure 7 show that, in the current setting, the latter type of insurance must in fact be better value than the former, up to and including year 4. However, in year 5 a threshold is crossed. In this year, assuming the bubble does not burst, an activist policy-maker observes the bubble continuing to grow to a size of 5 percentage points, at the same time as the sceptic's policy settings in previous periods have failed to prepare the economy for the bubble's possible future collapse. The combination of these developments sees an activist's expected cost-benefit trade-off shift suddenly from seeking to burst the bubble, by tightening policy, to seeking to cushion the economy against any future bust, by loosening policy. The decisiveness of the swing from one form of insurance to the other is, in part, driven by the fact that, in the current setting, any loosening in current policy increases the chances of the bubble surviving next period and growing further – so increasing the likelihood, in an activist's considerations, that he may have to cope with the collapse of a very large bubble indeed some time down the track.^[14]

To see how these findings change as a function of the economy's steady-state neutral nominal interest rate, Figure 8 shows the difference between the policy recommendations of activist policy-makers, with and without a ZLB constraint, for i* = 1, 3 and 8 per cent. Here, these activists assume again that policy can affect the bubble's period-to-period probability of bursting according to Equation (17) with δ = 0.2.

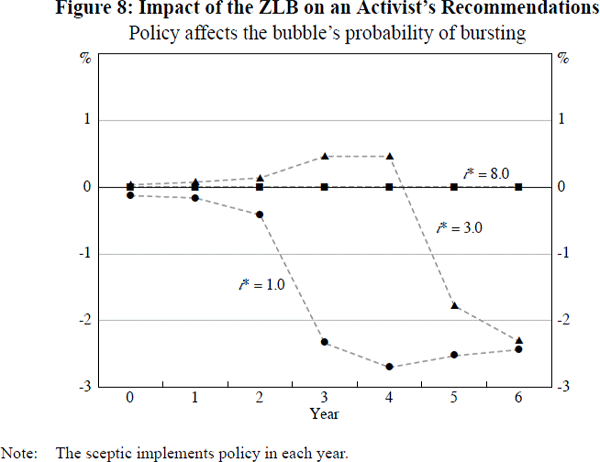
Interestingly, for the case where i* is extremely low, at 1 per cent, two differences are apparent relative to the case i* = 3 just discussed. The first is that, even in the early life of the bubble, the ‘ZLB effect’ is now marginally negative. The second is that the threshold described above, beyond which an activist shifts to recommending sharply looser policy than they would do in the absence of the ZLB, is now crossed earlier. On the other hand, we see that for values of i* far above zero, the ‘ZLB effect’ is once again negligible, even by the time the bubble has been growing for 6 years.

4.5 Sensitivity to Model Parameters

It is interesting to explore how sensitive the preceding results are to our choice of model parameters. We focus in particular on the two parameters β and λ. The former captures how responsive output is to real interest rates. The latter captures how ‘naturally self-correcting’ our Ball-Svensson economy is, absent any policy action.^[15]

Turning first to the case of β, we consider again the baseline case of an exogenous bubble with constant period-on-period probability of bursting p_t = 0.4 (except p₁₄ = 1), and constant growth in the event that it does not burst, γ_t = 1. We then consider the recommendations of activists in two different economies, each of which has a steady-state neutral nominal interest rate of 3 per cent, but which differ in their responsiveness to real interest rates – with values of β = 0.5 and 1.0 respectively. All other model and loss function parameters are assumed to take their baseline values: α = 0.4, λ = 0.8 and μ = 1.0.

We find that, for an economy with lower responsiveness, the impact of the ZLB on an activist policy-maker's recommendations is correspondingly greater when faced with an exogenous bubble. This is illustrated in Figure 9, which shows the difference between the policy recommendations of activist policy-makers, with and without a ZLB constraint, in the two economies.

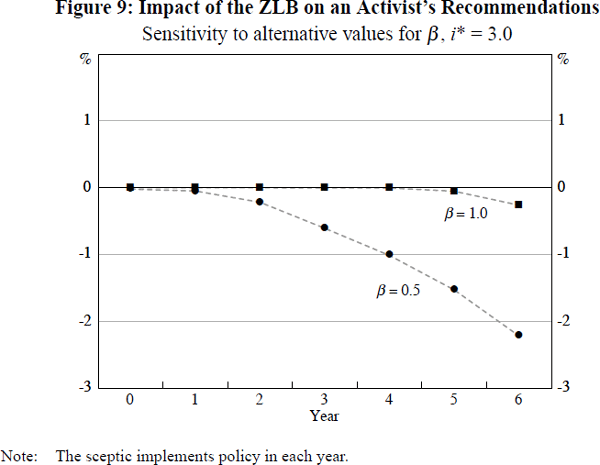
The direction of this result is unsurprising, since the capacity of policy to stabilise the economy following a large negative shock to output is weaker, the smaller is β. Hence, the activist in our β = 0.5 economy is commensurately more anxious, in each period, to begin building a buffer of added inflation and output against the bubble's eventual collapse, than his counterpart in the β = 1.0 economy.

What is perhaps surprising is the magnitude of this sensitivity, with the ‘ZLB effect’ exceeding 1 percentage point as early as year 4, in the economy with β = 0.5. By contrast, in the β = 1.0 economy, the corresponding ‘ZLB effect’ is still negligible in year 4, and only reaches 26 basis points in year 6.^[16]

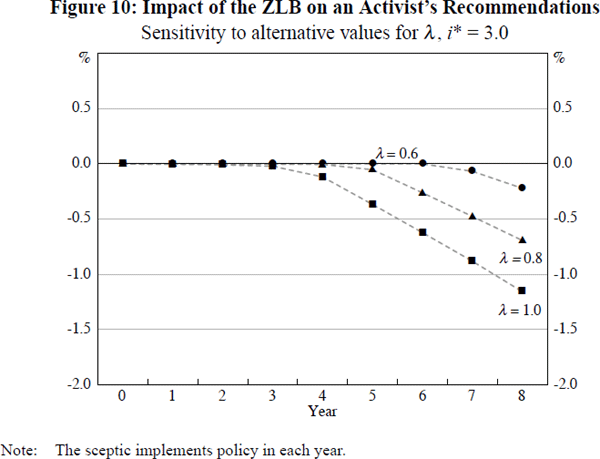
Correspondingly, to assess the sensitivity of an activist's policy recommendations to the value of λ, we consider the same baseline case of an exogenous bubble with constant period-on-period probability of bursting, p_t = 0.4 (except p₁₄ = 1), and constant growth in the event that it does not burst, γ_t = 1. Now, however, we consider the recommendations of activists in three different economies, each of which again has a steady-state neutral nominal interest rate of 3 per cent, but which this time differ in the degree to which output is naturally self-correcting in each – with values of λ = 0.6, 0.8 and 1.0 respectively.^[17]

In terms of our insurance framework for assessing the likely impact of the ZLB on an activist's recommendations, we would expect this impact to be greatest in the economy with λ = 1.0, and smallest in that with λ = 0.6. Policy-makers in the λ = 0.6 economy can expect considerable assistance in restoring output to potential, whenever the bubble bursts, from the economy's natural tendency to rebound from such a shock. By contrast, in the λ = 1.0 economy, policy-makers can expect no such assistance and so will wish to take out commensurately more insurance against the possible effects of the bubble's future collapse.^[18]

This is indeed what we find, as illustrated in Figure 10, which shows the difference between the policy recommendations of activist policy-makers, with and without a ZLB constraint, in each of our three economies. This time, however, the variation in the impact of the ZLB across our three economies is not substantial, at least until the bubble has grown very large, which suggests that our earlier results are fairly robust to plausible changes in the value of λ.^[19]

Footnotes

Note that, to ease the process of numerically determining optimal paths of contingent policy recommendations for an activist policy-maker in each period, we actually make the simplifying assumption here and subsequently that, if the bubble survives until year 14 (which is an extremely unlikely event for all the parameter values we consider), then it bursts with certainty in that year. Hence, strictly speaking, our assumption regarding p_t here is that p_t = p* = 0.4 for all t = 0,1,…,13, while p₁₄ = 1. Also, for reference, if p_t were 0.4 for all t this would imply an average remaining life for the bubble of two and a half years. Since we assume p₁₄ = 1 here, however, our exogenous bubble in this subsection has an expected remaining life in year 0 of just under two and a half years. [7]

Since i* = r* + π*, this might represent an economy where the neutral real rate, r*, is 2 per cent, and target inflation, π*, is 1 per cent; or where r* = 3 per cent and π* = 0 per cent; or any other such combination. [8]

A variation which we do not consider further here, but which we have examined in detail, is the case of rational bubbles. See Appendix C for a brief discussion of this case. [9]

Note that an activist's policy recommendations themselves are, however, tighter in every period for a bubble with p_t = p* = 0.2 than for a bubble with p_t = p* = 0.4. This is true with or without the ZLB constraint on nominal interest rates – for the case without the ZLB constraint see Gruen et al (2003), Figure 2. [10]

We choose the functional form in Equation (16) so that, for the benchmark policy settings chosen by the sceptic, γ_t = 1 for all t, as in the exogenous bubble case. Note also that in Equation (16) the growth of the bubble this period depends upon last period's interest rate. An interesting variant, suggested to us by Kenneth Kuttner, would be to allow for monetary policy to have a contemporaneous impact on asset prices (while continuing to affect the output gap directly with a 1-period lag). If suitably incorporated, such a change might allow policy-makers to provide a brake on the fall of asset prices whenever a bubble burst, so cushioning the impact of the burst on aggregate demand. However, knowledge that the monetary authorities might behave in this way might risk creating a moral hazard problem along the lines of the so-called ‘Greenspan put’ discussed in relation to the recent tech stock boom and bust in the United States. For reasons of space, we do not pursue these issues further here. [11]

To continue holding the bubble's growth to zero, while it survives, would of course require policy to be set 1 percentage point higher than the sceptic in each such period – with the usual consequences of tight policy for both output and inflation. [12]

The claim of a stronger effect is based on comparing the difference between the ‘Activist (ϕ = 1, ZLB)’ and ‘Activist (ϕ = 1, no ZLB)’ lines in Figure 5, on the one hand, with that between the ‘Activist (ZLB)’ and ‘Activist (no ZLB)’ lines in Figure 2, on the other. [13]

For a further discussion of this threshold effect, the factors determining its precise timing, and its sensitivity in particular to the value of the model parameter λ, see also Appendix C. [14]

The smaller is λ, the more swiftly will output in the economy rebound towards potential, of its own accord, following a shock. Conversely, if λ = 1.0, the economy has no innate propensity to correct either a positive or negative output gap once it opens up, so that the full burden of stabilising the economy falls upon policy-makers setting the real interest rate. [15]

In the β = 0.5 economy, the ‘ZLB effect’ is sufficiently strong that, if the bubble were to survive this long, an activist policy-maker's recommendations would actually reach the ZLB by year 7. [16]

Here we revert to the assumption that β = 1.0 in all three economies, with the parameters α and μ again at their baseline values of 0.4 and 1.0. [17]

The same conclusion can be reached more formally in terms of the phase diagram for the Ball-Svensson model discussed in Section 3, and derived in Appendix B. It may readily be checked that, for 0 ≤ λ ≤ 1, increasing the value of λ makes the slopes of both the boundary lines separating regions I, II and III more negative. Hence, increasing λ brings both regions II and III, which an activist policy-maker wishes to stay away from, closer to the origin in (y_t, π_t)-space and so increases the incentive for such an activist to recommend looser policy than otherwise, to shift the economy upwards and to the right, away from these danger zones. [18]

See also Appendix C for a brief discussion of how a change in the value of λ affects the recommendations of an activist policy-maker in the case of an endogenous rather than exogenous bubble. In this case the point noted in Footnote 6 becomes relevant, that the attractiveness of insuring against encountering the ZLB by building a buffer of higher output and inflation becomes a function of λ. [19]