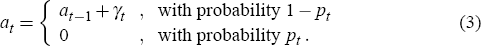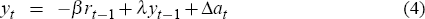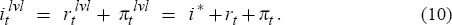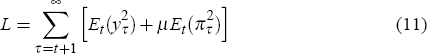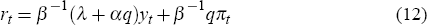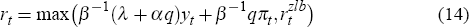RDP 2005-04: Monetary Policy, Asset-Price Bubbles and the Zero Lower Bound 2. Methodology

2.1 The Augmented Ball-Svensson Model

The starting point for our analysis is a simple model of a closed economy, due to Ball (1999a) and Svensson (1997). This model is described by two equations:

where y is the output gap, r is the difference between the real interest rate and its neutral level, π is the difference between consumer-price inflation and its targeted rate, and α, β, and λ are positive constants (with λ ≤ 1 so that output gaps do not behave explosively with real interest rates at neutral).

As noted in Gruen et al (2003), the Ball-Svensson model ‘has the advantage of simplicity and intuitive appeal … It assumes, realistically, that monetary policy affects real output, and hence the output gap, with a lag, and that the output gap affects inflation with a further lag’. We adopt the same baseline values for the parameters α, β, and λ as those chosen by Ball, for the case where each period in the model corresponds to one year, namely α = 0.4, β = 1 and λ = 0.8.^[2]

Next, exactly mirroring Gruen et al (2003) for the present, we augment the model with an asset-price bubble. We assume that in year 0 the economy is in equilibrium, with both output and inflation at their target values, y₀ = π₀ = 0, and that the bubble has zero size, a₀ = 0. In subsequent years, we assume that the bubble evolves as follows:

Thus, in each year, the bubble either grows by an amount, γ_t > 0, or bursts and collapses back to zero. We also assume that, once the bubble has burst, it does not re-form. To allow for the effect of the bubble on the economy, we modify the Ball-Svensson model to read:

In each year that the bubble is growing it has an expansionary effect on the economy, increasing the level of output, and the output gap, by γ_t. The bubble is, however, assumed to have no direct effect on consumer-price inflation, although there will be consequences for inflation to the extent that the bubble leads the economy to operate with excess demand as it expands, and with excess supply when it bursts. When the bubble bursts, the effect on the economy is of course contractionary: if the bubble bursts in year t, the direct effect on output, and the output gap, in that year will be 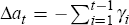. Thus, the longer the bubble survives, the greater will be the contractionary effect on the economy when it bursts.^[3]

Equations (3), (4) and (5) describe the model used by Gruen et al (2003), and are adopted again here. In a moment we shall also incorporate a ZLB on the nominal interest rate into the model, but before doing so it is worth remarking on a number of aspects of the model so far.

The most notable feature of Equations (3), (4) and (5) is that the treatment of both the asset-price bubbles and the structure of the economy is deliberately kept extremely simple and stylised. For example, the model allows for no forward-looking element in the formation of inflation expectations, so limiting the scope for monetary policy to influence the economy through pre-commitment to a particular monetary policy path or approach. Furthermore, the asset-price bubbles in the model are treated in a simple, reduced-form fashion, in terms of their impact on real activity, without any attempt to model the bubble formation process itself.

The reason for these choices is that much of the discussion about how monetary policy should react to asset-price bubbles focuses on the extreme informational difficulties that policy-makers face in determining the properties of a given bubble (current size, likelihood of collapse), or whether a bubble even exists. These informational difficulties are often cited as a principal reason why an activist approach to monetary policy in the face of asset-price misalignments might be difficult or sub-optimal in practice. However, by using a highly simplified model of the economy, in which policy-makers are also endowed with full knowledge of the stochastic properties of a developing asset-price bubble, Gruen et al (2003) were able to abstract from these informational issues. By doing so, they were able to demonstrate that there are other factors, besides informational constraints, which complicate an approach of actively responding to asset-price bubbles – making it difficult sometimes even to know whether policy ought to be set more tightly or more loosely than it would otherwise be.

Our adoption in this paper of the same simplified modelling framework as Gruen et al (2003) should be viewed in the same spirit. In particular, the reason that we do not attempt to provide a more explicit or detailed model of asset prices in this paper is simply that doing so is not a focus of the paper. Rather, extending the work of Gruen et al, we wish to study whether or not it is clear-cut in what way the presence of a ZLB on nominal interest rates would influence policy-makers, attempting to handle a developing asset-price bubble, even when in possession of a good understanding of the stochastic properties of the bubble's likely future impact on the real economy. The same rationale applies to our choice of a simple and transparent modelling framework which excludes any forward-looking element to the inflation expectations formation process. Excluding such an element does not imply that the management of future expectations might not be an important tool in the armoury of a central bank, especially as the economy approached the ZLB. Rather, it simply reflects that our aim in this paper is to highlight other factors which would – even were such management of future expectations possible – still complicate the task of policy-makers trying to determine how, optimally, to respond actively to a developing bubble.

Returning to the model itself, last but not least we introduce a ZLB on the nominal interest rate into the model described by Equations (3), (4) and (5). It is at this point that our treatment diverges from that in Gruen et al (2003).

In Gruen et al the simplifying assumption is made that policy-makers control the real interest rate, rather than the nominal one, and that this real interest rate can be adjusted arbitrarily in response to shocks to the economy. Here we drop this latter assumption and require, instead, that the real interest rate never be such that the corresponding level of the nominal rate would be negative.

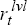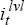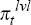This requirement may be expressed mathematically by introducing variables , and for the respective levels of the real interest rate, nominal interest rate and rate of inflation. Then, writing r*, i* and π* for the corresponding neutral or target levels of these variables, the ZLB restriction simply becomes the requirement that

while the following four identities, primarily relating real and nominal variables, must also be satisfied:

2.2 Activist and Sceptical Policy-makers

Equations (3) to (10) summarise our Ball-Svensson economy, experiencing an asset-price bubble, and subject to a ZLB on nominal interest rates. Returning to the framework employed by Gruen et al (2003), we next introduce two different types of policy-maker: sceptics, who don't try to second-guess asset-price developments; and activists, who believe that they understand enough about asset-price bubbles to set policy actively in response to them.

To draw the distinction more precisely, both types of policy-maker understand how the output gap and inflation evolve over time, as summarised by Equations (4) and (5). Activists also understand, and respond optimally to, the stochastic behaviour of the bubble, as summarised by Equation (3). Sceptics, by contrast, respond to asset-bubble shocks, Δa_t , when they arrive, but assume that the expected value of future shocks is zero.

Such sceptics should not, however, be thought of as naive or ignorant for adopting this position. As asset prices rise, there is always disagreement about whether the rise constitutes a bubble, in which case expectations about future asset-price changes may be non-zero, or are instead consistent with an efficient market, in which case the expected value of future changes in the asset price is zero.^[4] In holding that the expected value of future asset-price shocks is zero, sceptical policy-makers in our framework should simply be viewed as believers in the efficient markets hypothesis.

Continuing, we assume that policy-makers observe in each year whether the bubble has grown further, or collapsed, before setting the interest rate for that year. Given the nature of the lags in the model, this year's interest rate will have no impact on real activity until next year, and on inflation until the year after that.

We also assume that our two types of policy-maker have the same preferences, and care about the volatility of both inflation and output. Explicitly, we thus assume that in each year t, policy-makers (whether activist or sceptic) recommend the real interest rate, r_t, which will minimise the weighted sum of the expected future squared deviations of inflation and output from their target levels:

where μ is the relative weight on the deviations of inflation and E_t is the policy-maker's year t expectation. For the baseline results in this paper we set μ = 1 so that policy-makers are assumed to care equally about deviations of inflation from target and of output from potential.

Finally, in the absence of a ZLB on nominal interest rates, it is possible to write down explicitly the form that optimal policy will take for a sceptic in our Ball-Svensson economy.^[5] Ball (1999a) showed that this is given by a Taylor rule, namely

where the scalar q is defined by q = (− μα + (μ²α² + 4μ)^½)/2. For our baseline parameter values, this becomes

which is a more aggressive Taylor rule than the ‘standard’ one introduced by Taylor (1993), r_t = 0.5y_t + 0.5π_t.

In the presence of a ZLB on nominal interest rates, however, it may not be possible for a sceptic (or an activist, after the bubble has burst) to recommend policy in accordance with Equation (12). Instead, optimal policy for such a policy-maker must now take the form

where 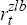denotes the value of r_t which corresponds to 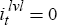, namely

Footnotes

Ball chose these parameter values to fit the US economy, based on previous studies by Ball (1994), DeLong and Summers (1988) and Rudebusch (1995). Ball (1999b) also subsequently used these same parameter values in an open-economy version of the model which he noted was ‘meant to apply to medium-to-small open economies such as Canada, Australia and New Zealand’ (although an increase in the real interest rate, for example, affects output through two channels in this open economy model – directly and via the exchange rate – rather than just via the former channel). Finally, Ball and Svensson also added white-noise shocks to each of their equations, which we have suppressed for simplicity. [2]

There is nothing special about our assumption in Equations (3) and (4) that, when the bubble bursts, it imparts a negative shock to the economy equal to the sum of the positive shocks it has previously imparted. We adopt this assumption merely for its simplicity and convenience. An interesting alternative, but one which we do not explore further in this paper, would be to introduce an asymmetry into the bubble's economic impact. In this case the negative shock to the economy when the bubble bursts would instead exceed the bubble's size immediately prior to the collapse, in keeping with the idea that excess economic expansion during the growth phase of a bubble could be associated with significant ongoing impediments to economic activity after it bursts. For a model which incorporates such asymmetry, and discussion of some of its possible implications, see Kent and Lowe (1997). [3]

In the late 1990s, precisely this debate was occurring within the US Federal Reserve in relation to the US stock market, as the following quotation from Stephen Cecchetti makes clear.

From August 1997 to June 1999 I sat on the backbench at the meetings of the FOMC and received all of the material distributed to the participants … The interesting thing is that during the period when I took part in this process, the Board staff preparing the forecasts invariably assumed that the US stock market would decline significantly – 10 to 20 per cent declines in the Wilshire 5,000 index were commonly the basis for the forecasts. They clearly believed that the stock market was overvalued …
At the time this was all happening, I confess that I was scandalised. I regularly ranted about the practice of forecasting a dramatic decline in the stock market. Like the vast majority of academics, I adhered to the efficient markets view … while we needed to assume something about the stock market, shouldn't we assume the equity index would stay constant at its current level indefinitely? …
This happened five years ago (which is why I can talk about it now), and in the interim I have changed many of my views. (Cecchetti 2003)

Sceptical policy-makers in our framework may be characterised as those who adhere to the approach of Cecchetti – before his change of view!

[4]

This reflects that, in the absence of the ZLB, certainty equivalence holds in the model for a policy-maker who expects no future asset-price shocks. Such policy-makers in fact include not only sceptics in each period, but also activists once the bubble bursts (since it is assumed never to re-form). [5]