RDP 2005-04: Monetary Policy, Asset-Price Bubbles and the Zero Lower Bound 3. How Might the Zero Lower Bound Influence an Activist Policy-maker?

In Section 4 we present numerical simulations that examine how the presence of a ZLB on nominal interest rates influences the policy recommendations of an activist policy-maker, confronting a developing asset-price bubble. We also explore the implications of our simulation results for policy questions such as the appropriate choice of inflation target, and how this may depend on key economic parameters which may vary from country to country.

Before turning to these results, however, it is instructive to ask: what effect, intuitively, would we expect the existence of the ZLB to have on an activist policy-maker weighing how best to respond to an asset-price bubble? In the remainder of this section we address this question in two stages: first for asset-price bubbles whose development (period-to-period growth and/or probability of bursting) is completely exogenous; and secondly for asset-price bubbles whose development can be influenced by policy.

Note that our focus here, and throughout what follows, is on the marginal effect which the ZLB might have on an activist policy-maker, over and above whatever impact the bubble itself would have even in the absence of a ZLB on nominal interest rates. Thus, when we refer to the ZLB causing an activist to (say) loosen policy in a given period, we are not necessarily implying that they would recommend policy which is actually looser than a sceptic in that period. Rather, we mean simply that they would recommend policy, in that period, which is not as tight as they would otherwise recommend, were there no ZLB.

3.1 Exogenous Bubbles

Consider an asset-price bubble whose period-to-period growth and probability of bursting are entirely exogenous, unaffected by monetary policy. Suppose also that an activist policy-maker understands that he is powerless to influence the future trajectory of this bubble.

As such a bubble grows, the activist appreciates the increasing risk that, in the future, its eventual bursting will generate a large negative shock to output and, thereafter, to inflation, which might result in the activist's preferred post-bubble policy recommendations striking the ZLB. This latter effect could occur either: immediately, if the output gap is driven sufficiently negative to result in the optimal nominal interest rate falling below zero in the period of the bubble's collapse; or in subsequent periods, as the shock to output flows into lower inflation (or even deflation), so that a lower nominal interest rate is required to reach a desired real interest rate setting.

Such a situation, in which the policy-maker's capacity to stabilise the economy would be constrained, would clearly be sub-optimal. Indeed, in the extreme, it might even result in the economy entering a deflationary spiral from which, owing to the ZLB, monetary policy acting via interest rates alone would be unable to rescue it. Intuitively, therefore, an activist policy-maker would prefer to prevent such an outcome arising in the future – even at some definite present cost in terms of their loss function, Equation (11).

In our Ball-Svensson model, however, the only available defence against such an outcome, for an exogenous bubble, is to recommend policy so as to raise both the output gap and inflation a little, relative to what would otherwise be optimal in the absence of the ZLB. Such a cushion of extra output and inflation would reduce the likelihood of policy subsequently striking the ZLB, either in the immediate aftermath of the bubble's collapse, or in subsequent periods. Hence, one would expect an activist policy-maker, concerned about the ZLB, to be marginally less hawkish than otherwise during the growth phase of an exogenous asset-price bubble.

An obvious caveat to this intuition concerns whether the notion of a buffer of extra inflation would, in practice, prove to be illusory. The possibility of generating such a buffer is clearly, to some degree, specific to our model economy, with its purely backward-looking inflation expectations. These backward-looking expectations mean that an activist policy-maker can expect higher inflation engineered in advance of a bubble's collapse to provide increased scope (owing to the persistence of inflation) to lower real interest rates in the aftermath of such a collapse, thereby stimulating the economy. To the extent that inflation expectations were only partially backward-looking, this would reduce the extent of the ongoing buffer which policy-makers would be able to generate for a given shift in interest rates – and so reduce the attractiveness of this policy option.

Setting aside this caveat for the present – which might alter the details of the results in Section 4, but not their overall thrust – the intuition just described may be neatly illustrated using a phase diagram for the Ball-Svensson model introduced by Reifschneider and Williams (2000). This phase diagram depicts how (y_t, π_t)-space may be sub-divided into three distinct regions, in each of which monetary policy has a differing capacity to return the economy to steady state (output at potential and inflation at target), in the absence of future shocks. This phase diagram is shown in Figure 1 below, for the case where α, β, λ and μ take their baseline values. A detailed derivation of this phase diagram, which differs from that provided by Reifschneider and Williams (2000), is set out in Appendix B.

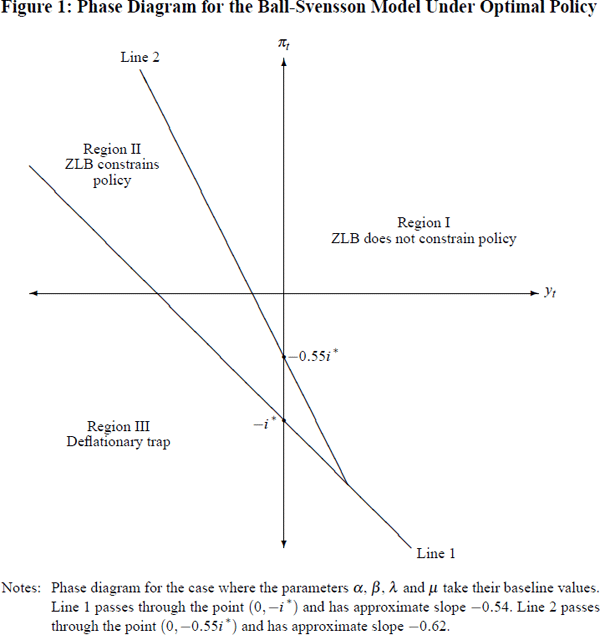
In region I, monetary policy is able to return the economy to steady state (absent future shocks), without ever striking the ZLB on nominal interest rates. By contrast, in region II, monetary policy is still able to return the economy to steady state (absent future shocks), but is initially constrained in doing so by the ZLB – so that the economy's path back to (y_t, π_t) = (0,0) would be sub-optimal (higher loss), relative to that which could be achieved if nominal interest rates were not bounded below. Finally, in region III, monetary policy operating via interest rates alone is unable to prevent the economy entering a catastrophic deflationary spiral. Such a fate would only be able to be averted by the advent, as a supplement to expansionary monetary settings, of sufficiently powerful future positive shocks to the economy: either exogenous, such as a boom in world growth; or generated through other arms of policy, such as a fiscal expansion.

Now consider again an activist policy-maker in our Ball-Svensson economy, confronted with a developing exogenous asset-price bubble, and with no policy tools at his disposal other than the interest rate. Clearly, he will wish to take whatever steps are necessary to prevent the economy ever entering region III – since this would inescapably result in devastating future losses. He will also prefer to keep the economy from entering region II, since in this region the ZLB would prevent output and inflation from being returned to steady state as efficiently as possible, so incurring additional costs in terms of his loss function, Equation (11).

If we combine these observations with the fact that, whenever the bubble does burst, the nature of the resultant shock to the economy will be to shift it horizontally to the left in (y_t, π_t)-space, by an amount equal to the size of the bubble, then the incentives for our activist policy-maker become clear. To ensure that the economy never enters region III, and to also keep it out of region II if possible, he will prefer to recommend policy, while the bubble survives, which pushes the economy up and to the right in (y_t, π_t)-space, relative to what he would recommend were there no ZLB. He will prefer this even if it may take the economy further away from steady state at (y_t, π_t) = (0,0), and so incur an immediate cost in terms of his loss function, Equation (11).

Finally, Figure 1 also highlights two further points about the extent to which the ZLB will influence an activist policy-maker's interest rate recommendations. The first is that, the bigger the current size of the bubble, the further such a policy-maker will wish to push the economy upwards and to the right in (y_t, π_t)-space to minimise its chances of being driven into regions II or III whenever the bubble does collapse. Hence, the bigger the current size of the bubble, the greater will be the influence which the ZLB will have on an activist's policy recommendations.

The second point rests on the observation that the locations of the boundary lines separating regions II and III from the rest of (y_t, π_t)-space are both determined by the level of the neutral nominal interest rate, i*. The higher is i*, the further these boundary lines will be pushed down and to the left, away from the origin in (y_t, π_t)-space – so reducing the risk perceived by an activist policy-maker of the economy being driven into either of these regions. This will in turn reduce an activist's need to recommend interest rate settings, while the bubble survives, which hold both the output gap and inflation higher than they would otherwise prefer.

This latter point is of course simply another way of saying that the higher are both the neutral real rate of interest in the economy and the target rate of inflation, the less of a factor will the ZLB be in the minds of policy-makers when dealing with an asset-price bubble. Hence, while there are clearly costs associated with operating the economy at too high an average inflation rate, policy-makers may also wish to take care not to adopt too low a figure when deciding upon an inflation target – especially if the neutral real interest rate in their economy is relatively low.

3.2 Bubbles Whose Development is Affected by Policy

For an entirely exogenous asset-price bubble, we have just seen that the presence of a ZLB on nominal interest rates creates an incentive for an activist policy-maker to recommend somewhat looser policy than otherwise, so as to shift the economy upwards and to the right in (y_t, π_t)-space. The optimal extent of such insurance against striking the ZLB will be greater the larger is the current size of the bubble, and the lower is the economy's neutral nominal interest rate in steady state.

For a bubble whose development (period-to-period growth and/or probability of bursting) is affected by policy, however, the situation is no longer so clear. Consider first the case of a bubble whose probability of bursting next period is increased (decreased) by setting policy more tightly (loosely) in the current period.

In this event, although the marginal effect of loosening policy would be to shift the economy away from regions II and III in (y_t, π_t)-space, it would also be to increase the odds of the bubble surviving and growing next period, so posing a greater risk down the track. Hence, the direction in which the ZLB would influence the recommendations of an activist policy-maker is no longer clear-cut. Indeed, for a bubble which was very sensitive to policy, one could imagine the ZLB providing an incentive for an activist policy-maker to raise interest rates decisively early in the bubble's life – in the hope of bursting it before it could grow sufficiently to pose a serious threat to the stability of the economy upon its collapse.

A similar story holds for the case of a bubble whose period-to-period growth, while it survives, may be influenced by policy. Suppose that an activist policy-maker knows that the bubble's growth next period, if it survives, will be reduced (increased) by setting policy more tightly (loosely) in the current period.

In this event, loosening policy in any given period would again have the effect of shifting the economy away from regions II and III in (y_t, π_t)-space – by a greater amount, indeed, should the bubble survive, than the same loosening would achieve in the case of a purely exogenous bubble. However, it would also have the effect of further boosting the size of the bubble, in the event that it did not burst next period, hence increasing the size of the negative shock to the economy whenever the bubble ultimately does burst. Hence, once again, the direction in which the presence of a ZLB on nominal interest rates would, at the margin, push an activist policy-maker in this situation is no longer clear.^[6]

3.3 An Insurance Interpretation for the Implications of the ZLB

The observations in Sections 3.1 and 3.2 may be neatly summarised in terms of the phase diagram, Figure 1, and an ‘insurance’ paradigm for thinking about how the presence of a ZLB on nominal interest rates might influence the thinking of an activist policy-maker. As illustrated in Figure 1, the presence of a ZLB creates two zones in (y_t, π_t)-space, regions II and III, which an activist policy-maker will be either desperate (region III) or at least anxious (region II) to keep away from. As an asset-price bubble grows, such a policy-maker will therefore wish to take out some insurance against the economy being driven into either of these regions whenever the bubble finally does collapse.

For the case of an exogenous bubble, the only such insurance which an activist can set out to purchase – that is, obtain at some definite cost in terms of their loss function, Equation (11) – is to manoeuvre the economy upwards and to the right in (y_t, π_t)-space, by recommending policy be set more loosely than otherwise.

For a bubble whose development (period-to-period growth and/or probability of bursting) is affected by policy, however, alternative potential forms of insurance are available besides this standard type. If the bubble's probability of bursting is influenced by policy, this alternative insurance takes the form of increasing the odds that the bubble will collapse while it is still young, before it has grown big enough to drive the economy into regions II or III through its collapse. If instead the bubble's growth may be curtailed by running policy more tightly, it takes the form of restraining the potential future size of the bubble, so as to again ensure that the negative shock which the bubble imparts upon bursting will not be large enough to drive the economy into regions II or III.

In both these latter cases, these alternative forms of insurance entail setting policy more tightly than otherwise, rather than more loosely, as was the case for the standard form of insurance. For endogenous bubbles, therefore, it is no longer clear a priori which form of insurance an activist policy-maker will prefer to purchase, and therefore in which direction the ZLB will alter his policy recommendations. This will depend upon the relative costs and benefits of the different forms of insurance available – which will, in turn, vary from period to period, reflecting the state in which the activist finds the economy (current output gap and inflation rate, as well as current size of the bubble) when deciding his preferred policy settings.

Footnote

Note that for the endogenous bubbles described in this sub-section, the cost-effectiveness of the strategy of building a buffer of higher inflation and output would also now be a function of the parameter λ, which captures the degree to which our Ball-Svensson economy is ‘naturally self-correcting’. This will be so even while such a bubble is still small, which is not the case for an exogenous bubble. To see this, note that, in an economy with (say) a lower λ, any buffer of higher output would erode more quickly each year. However, an activist policy-maker in such an economy, being aware of this, could simply counteract this erosion by running policy commensurately more loosely, so as to maintain the same overall buffer – at least until such an approach became constrained by the ZLB (because the desired buffer had become sufficiently big in the face of a large bubble). For an exogenous bubble, such behaviour would incur no additional loss, since our policy-makers' loss function, Equation (11), contains no penalty for interest rate volatility. By contrast, for a bubble whose probability of bursting or future growth is influenced by policy, the need for such ongoing additional policy easing, to maintain a given buffer of output and inflation, would no longer be costless since it would increase either the bubble's future size or its probability of surviving into subsequent periods. [6]