RDP 2003-09: Housing Leverage in Australia 4. Econometric Model and Results
July 2003
- Download the Paper 605KB
4.1 Model and Methodology
The only households with positive leverage are those that currently have debt against their home. By definition, leverage cannot be negative, so its distribution is censored at zero. The full sample of households also contains a large fraction of renters and outright homeowners who have no owner-occupied leverage. Although tobit techniques can be used to estimate some censored samples, they are inappropriate in the current context. Tobit models require that the explanators of whether the household has any leverage at all are the same as the determinants of its level. However, characteristics of the loan can be (and here turn out to be) important determinants of the level of leverage, but they are undefined for households without housing debt. Therefore they cannot also be used to explain whether or not a household has any leverage.
On the other hand, estimating a model of leverage only over the sub-sample with debt does not allow assessment of the whole population's behaviour. Gronau (1974) and Lewis (1974) showed that a censored sample may have unrepresentative characteristics relative to the whole population. Since this can bias OLS parameter estimates (Heckman 1976, 1979), we therefore model leverage using an appropriately specified selection model, which corrects for this bias.
Table 1 illustrates that the leveraged sub-sample of the dataset used here could be unrepresentative. Households with housing debt have quite different age and income characteristics than the whole sample. The probability of having a mortgage is greatest for those aged 35–39, irrespective of household income. As income increases, so does the probability of having a mortgage. These two features imply that the sub-sample of households with a mortgage is likely to have a higher median income than the general population, and an over-representation of middle-aged household heads.
| Age group | Income quintile | ||||
|---|---|---|---|---|---|
| Q1 | Q2 | Q3 | Q4 | Q5 | |
| 20–24 | 9.2 | 9.9 | 17.6 | 29.8 | 39.3 |
| 25–29 | 12.3 | 14.2 | 35.0 | 44.5 | 43.9 |
| 30–34 | 21.6 | 32.5 | 45.0 | 57.1 | 65.5 |
| 35–39 | 28.4 | 36.7 | 49.8 | 66.7 | 68.4 |
| 40–44 | 20.3 | 36.5 | 46.0 | 63.0 | 63.6 |
| 45–49 | 12.1 | 27.5 | 39.6 | 50.0 | 58.1 |
| 50–54 | 23.1 | 27.8 | 35.2 | 41.1 | 46.0 |
| 55+ | 3.7 | 4.5 | 12.7 | 21.6 | 23.2 |
Heckman (1976) proposed a two-step procedure to correct for selection bias, involving modelling of the rules that determine inclusion into the sample. The results from these selection models are then used to adjust the estimates for the equation of interest so that they capture population responses rather than those of the sub-sample over which they are estimated.[6] Households with owner-occupied leverage select themselves into this group by both owning their home and having some debt secured against it. Thus our model involves two selection rules: the tenure decision on whether or not the household owns rather than rents their home; and the mortgage decision on whether or not the household has housing debt.
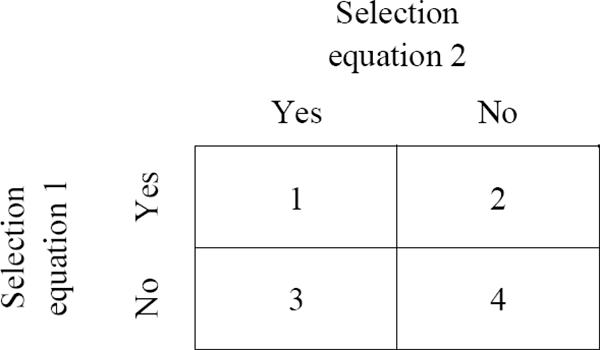
The error structure of the model depends crucially on whether the two decisions are made sequentially or jointly. The distinction between sequential and joint decisions relates to the interdependency of the two decisions, rather than their timing, as illustrated in Figure 5. If the two decisions are defined over the entire set of observations, so that all four cells are logically possible, then they are made jointly, regardless of whether all the outcomes represented by the cells are actually observed (Lee and Maddala 1985; Tunali 1986). The standard case of choices about education and labour supply is an example of a joint decision process (Fishe, Trost and Lurie 1981); an individual could choose to enter the labour force or not regardless of whether they had previously completed a particular level of education. Sequential decisions, on the other hand, are characterised by one decision only being defined given a particular outcome of the other decision (Maddala 1986). This is the case with our sample selection rules; a household cannot ‘decide’ to have a mortgage on an owner-occupied property if they are not owner-occupiers; cell 3 is infeasible.
Given this structure for the selection rules, we have a system in which the tenure selection
equation is used to adjust the mortgage selection equation, which is only defined if the
household is a homeowner (Ti = 1). These selection equations are estimated
using maximum-likelihood probit techniques. As in all probit models, the selection equations
assume that the observed decisions Ti and Mi reflect the
values of unobserved latent variables 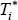 and
and 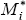 . If
. If 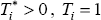 (the
household is an owner-occupier) while if
(the
household is an owner-occupier) while if 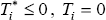 and the household rents.
Similarly if a home-owning household i has housing debt, then Mi =
1, implying
and the household rents.
Similarly if a home-owning household i has housing debt, then Mi =
1, implying 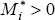 .
.
The results from the selection equations can then be used to adjust the equation explaining leverage (levi), as shown in Equation (2), so that OLS estimates of β are consistent, although they are inefficient compared to maximum likelihood techniques. The second-stage OLS estimates of the error variance and covariance matrices are biased, but we make an approximate correction for this using the delta method (Heckman 1979; Tunali 1986). The parameter estimates are also quite sensitive to violations of the underlying normality assumptions; our preferred specifications preserve normality, but possibly at the cost of some efficiency.
The additional variables λ1 and λ2 in the
leverage equation capture the effect of selection on the error term: 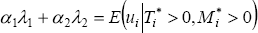 .
Because this is a double-selection model, they are not identical to the inverse Mills ratio in a
standard Heckman-Lee single-selection model.
.
Because this is a double-selection model, they are not identical to the inverse Mills ratio in a
standard Heckman-Lee single-selection model.
Precise estimation of parameters depends on the three equations being sufficiently identified, which requires that the sets of explanators Z1, Z2 and X have at least some non-overlapping variables, so that the regressors for one equation are not simply capturing the same information as the selection terms (λi). Our preferred specification involves several variables, such as user cost of housing, that are specific to one of the selection equations. It is nonetheless difficult to be certain that robust identification has been achieved; the significance of the selection terms in the leverage equation was sensitive to the inclusion in the selection equations of some statistically insignificant variables. The need to ensure identification and avoid multicollinearity result in a tendency to favour parsimonious specifications for our model, relative to the richness of the HILDA dataset.
The residual in the tenure equation, e1i, is assumed to
be distributed as a standard normal; e2i is also standar
normal, but defined only on the subpopulation 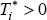 ; and
Vi is normally distributed on the subpopulation
; and
Vi is normally distributed on the subpopulation 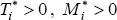 with variance
with variance 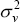 (Lee and Maddala 1985). The three errors may be
correlated; the technique used here allows for this. Many of the unobserved factors explaining
past mortgage repayments, and thus whether a mortgage has now been paid off, will be unrelated
to the past tenure decision. There are, however, good reasons to suspect that
e1i and e2i
could be correlated. At least some households' decisions to rent are driven by their
inability to obtain housing finance. Financial institutions' willingness to lend might
depend on variables that are not observed in the HILDA dataset such as savings history, past
loan defaults and so on. Their influence would therefore end up in the residuals of both
selection equations.
(Lee and Maddala 1985). The three errors may be
correlated; the technique used here allows for this. Many of the unobserved factors explaining
past mortgage repayments, and thus whether a mortgage has now been paid off, will be unrelated
to the past tenure decision. There are, however, good reasons to suspect that
e1i and e2i
could be correlated. At least some households' decisions to rent are driven by their
inability to obtain housing finance. Financial institutions' willingness to lend might
depend on variables that are not observed in the HILDA dataset such as savings history, past
loan defaults and so on. Their influence would therefore end up in the residuals of both
selection equations.
4.2 Estimation Results
Table 2 shows the parameter estimates and Table 3 the prediction outcomes for the two selection equations. The fit and prediction rates are reasonable, and within only a few percentage points of results in previous studies of tenure choice in Australia (Bourassa 1994, 1995), despite the absence of information about important components of households' wealth portfolios in HILDA. As expected, age, income and other indicators of life-cycle such as marital status are important determinants of homeownership. Age, income and other financial indicators were also strong determinants of whether home-owning households had housing debt. The indicator variables of whether anyone in the household made a profit or loss in the form of rental income are highly significant in the mortgage equation. Households that made a profit on their rental properties were significantly less likely to have a mortgage on their owner-occupied property than households without such income. In contrast, households that made a rental loss – that is, their expenses, including interest, on any mortgages against the investment property exceeded rental income – were significantly more likely to also have a mortgage on their home.
| Tenure | Mortgage | Tenure | Mortgage | ||
|---|---|---|---|---|---|
| Personal characteristics of the household head and demographic variables | |||||
| Age | 1.4*** | −2.6*** | Married | 30.4*** | |
| Retired | −41.2*** | Born in UK | −10.5 | ||
| Born in Europe(a) | −22.3 | Father born in UK | −2.3 | 10.2 | |
| Father born in Europe(a) | 27.2** | Student | −8.5 | ||
| Group household | −71.1*** | Children at home | 7.5*** | ||
| Only speaks English at home | 25.5*** | Receives youth allowance | −118.0*** | ||
| Household means variables | |||||
| Income ($'000) | 1.6*** | 0.5*** | Income squared ($'000) | −0.8*** | −1.0*** |
| Income cubed | 1.5** | Interest income | −7.5*** | ||
| Casual job | −18.9** | Income adequacy | −10.8*** | ||
| Made profit on rental property | −22.1** | Made loss on rental property | 30.5*** | ||
| Financial and housing variables | |||||
| Time at address | 6.5*** | −2.7*** | Short saving time horizon | 12.1* | |
| Condition of home(b) | −26.0*** | Importance of home(b) | 7.5*** | ||
| Moves in last 10 years | 11.0*** | Not moved recently | 2.2 | ||
| Housing adequacy(b) | 13.0*** | Value of home | 0.02* | ||
| Small apartment block | −58.3*** | Tall apartment block | −91.0*** | ||
| Semi-detached dwelling | −59.1*** | Pays off credit card on time(b) | −5.6** | ||
| Has credit card | −35.6*** | No of bedrooms | 21.3*** | ||
| Took out institutional loan | 167.0*** | Relative cost of owning | −10.3*** | ||
| Location variables | |||||
| Inner Sydney | 24.5* | Non-metro NSW | 22.7** | ||
| Outer Melbourne | 29.8** | Non-metro VIC | 38.5*** | ||
| Outer Brisbane | 45.9*** | Non-metro QLD | 46.1*** | ||
| Outer Adelaide | 35.0*** | Inner Perth | 53.9* | ||
| Outer Perth | 46.7*** | Non-metro WA | 58.9*** | ||
| Log-likelihood | −4,064.955 | Correct prediction rate | 85.6% | 85.8% | |
|
Notes: ***, **, and * represent significance at 1, 5 and 10 per cent levels. |
|||||
| Tenure equation | ||||
|---|---|---|---|---|
| Actual | ||||
| Own | Rent | Total | ||
| Predicted | Own | 4,662 | 641 | 5,303 |
| Rent | 404 | 1,543 | 1,947 | |
| Total | 5,066 | 2,184 | 7,250 | |
| Mortgage equation | ||||
| Actual | ||||
| Mortgage | No mortgage | Total | ||
| Predicted | Mortgage | 2,197 | 463 | 2,660 |
| No mortgage | 258 | 2,148 | 2,406 | |
| Total | 2,455 | 2,611 | 5,066 | |
| Prediction rate for tenure equation = 85.6% Prediction rate for mortgage equation = 85.8% |
||||
The central results from the estimation of the equation for household housing leverage are contained in Table 4. Overall the results are reasonable, with our model explaining about 30 per cent of the variation in households' housing leverage and an F-test of the null hypothesis that all the coefficients are equal to zero rejected at all conventional levels of significance. The estimated parameters from the model correspond to the total effect of a one-unit change in that variable on leverage, expressed in percentage points of leverage. For variables that are also in the selection equations, this total effect includes the variable's effect on leverage through its effect on the probability that the household has leverage at all. Table 4 therefore also shows the marginal effects of these variables on leverage, conditional on the household having leverage, which can be calculated from the estimated coefficients on the selection terms using standard methods. For ease of interpretation, we split explanators in the equations into three categories of household characteristics – the stage of the household in the life cycle, household means, and characteristics relating to finance and housing – and a group of location dummies to control for region-specific effects and the effect of unexpected changes in housing prices on leverage. Other demographic variables that might be expected to be associated with leverage, such as the education level, occupation or gender of the household head, were insignificant and thus excluded from the final specification.
| Total | Marginal | Total | Marginal | ||
|---|---|---|---|---|---|
| Personal characteristics of household head and demographic variables | |||||
| Age | −0.6*** | −0.5 | Retired | −11.8** | −10.5* |
| Married | 3.3 | 3.2 | Divorced | −1.5 | −1.5 |
| De facto | 3.8 | 3.9 | Separated | 11.0*** | 11.0*** |
| Born in UK | −5.0* | −5.0* | Born in Europe(a) | 1.9 | 1.9 |
| Father born in UK | 4.9** | 4.6* | Father born in Europe(a) | −6.8*** | −6.9** |
| Student | 7.2 | 7.3 | |||
| Household means variables | |||||
| Income ($'000) | 0.07(c) | 0.04 | Income squared ($'000) | −0.2 | −0.1 |
| Income adequacy(b) | −1.1 | −0.7 | Satisfaction with pay(b) | 0.8*** | 0.8*** |
| Casual job | −7.1*** | −6.5*** | Fixed-term contract | −2.8 | −2.8 |
| Likelihood of losing job in next 12 months(b) | −0.03 |
−0.03 |
Had difficulty paying mortgage on time | 4.7** |
4.7** |
| Has rental income | 14.2*** | 14.2*** | Has imputed income | 1.0 | 1.3 |
| Financial and housing variables | |||||
| Time lived at address | −0.8*** | −0.7** | Planned pay off date | 1.0*** | 1.0*** |
| Ahead of mortgage repayment schedule | −5.4*** |
−5.4*** |
Satisfaction with neighbourhood(b) | −1.0*** |
−1.0*** |
| Long saving horizon | 4.0*** |
4.0*** |
Took out institutional loan to buy house | 18.2* |
12.6 |
| Attitude to borrowing | 1.1 | 1.1 | Attitude to risk(b) | −0.8 | −0.8 |
| Moves in last 10 years | 1.2 | 0.8 | No recent moves | −5.3*** | −5.3*** |
| Condition of home(b) | 3.0*** | 3.1*** | Not a first-home buyer | 6.2*** | 6.2*** |
| Semi-detached dwelling | 5.1** |
5.3** |
Pays credit card on time(b) | −1.2*** |
−1.2** |
| Location variables | |||||
| Inner Sydney | 5.4 | 4.5 | Outer Sydney | 13.9*** | 13.4*** |
| Non-metro NSW | 15.0*** | 14.2*** | Outer Melbourne | 14.7*** | 13.7*** |
| Non-metro VIC | 18.1*** | 16.8*** | Inner Brisbane | 22.1*** | 22.1*** |
| Outer Brisbane | 23.9*** | 22.4*** | Non-metro QLD | 23.2*** | 21.6*** |
| Inner Adelaide | 18.2*** | 18.2*** | Outer Adelaide | 21.0*** | 19.8*** |
| Non-metro SA | 28.5*** | 27.6*** | Inner Perth | 9.5 | 7.7 |
| Outer Perth | 21.0*** | 19.4*** | Non-metro WA | 19.2*** | 17.2*** |
| Inner Hobart | 2.8 | 2.8 | Outer-city TAS | 22.5*** | 22.5*** |
| Non-metro TAS | 42.2*** | 41.0*** | ACT | 24.0*** | 23.3*** |
| NT | 31.0*** | 31.0*** | House price growth | −0.1 | −0.1 |
| Tenure selection term | 2.4 | 2.4 | Mortgage selection term | 17.4(c) | 17.4 |
| Adjusted R2 | 0.278 | No of observations | 2,327 | ||
Notes: ***,**, and * represent significance at 1, 5 and 10 per cent
levels. |
|||||
4.2.1 Stage of the household in the life cycle
A household's stage in the life cycle should be a key explanator of a household's housing leverage. Taking the results in Table 1 at face value, one might expect housing leverage to rise as households purchase homes and acquire debt during their family formation years, and then fall as they repay this debt. Our results are, however, mainly suggestive of leverage falling monotonically as households move through the life cycle. A household head that is one year older is associated with up to 0.6 percentage points less leverage, while an age-squared term was negative but insignificant if included. This contrasts with the positive coefficient on age and negative coefficient on the square of age that would be required to obtain a hump-shaped profile.
A number of other variables are also suggestive of leverage falling as households move through the life cycle. For a given term for the mortgage, a move-in date that is one year earlier than an otherwise identical household implies that the household's housing leverage will be about 1.8 percentage points lower, since both the move-in date and the expected payoff date are then one year earlier. This suggests an important role for passive paydown of mortgages on schedule; households that are older and have lived in their homes for longer have lower leverage in part simply because they have had longer to pay their mortgage off. In addition, rising housing prices imply that mortgages taken out earlier were likely to be smaller, and thus a smaller proportion of the home's current estimated price. On the other hand, some households must be making explicit decisions about the end date of their mortgage; otherwise, move-in date and payoff date would not both be significant because they would then be more closely correlated. Indeed, the expected loan terms implied by the move-in and payoff dates are overwhelmingly shorter than the 20 to 25-year terms generally specified in loan contracts. These financial decisions are likely to be dependent on households' assessments of their ability to achieve the targeted payoff date, and thus on their incomes and means more generally. Nonetheless, the significance of the coefficient on expected payoff date in a multivariate setting indicates that these expectations are also in large part independent of income and other factors, instead capturing household preferences about debt duration and portfolios that are not explained by income and demographic variables alone.
The combined size and precision of the estimated coefficients on these two variables suggest that this passive paydown effect is more important than any pure age effect. On the other hand, the significance of the coefficient on age after controlling for these factors indicates that age on its own also plays a role in determining leverage. This might be because older households have had longer to accumulate wealth (something that we cannot measure using the first wave of HILDA). Moreover, other significant explanators of leverage also suggest a more explicit life-cycle interpretation. Married household heads and those in de facto relationships tend to have slightly higher leverage than homeowners that have never married, although the difference is not significant at conventional levels. Households with retired household heads were both significantly less likely to have a mortgage, and to have lower leverage than other households when they did.
4.2.2 The means of the household
Our expectation that leverage should rise with household means is generally supported by the data. For example, our main indicator of household means, household income, is positively related to leverage, although it is only statistically significant at the 11 per cent level. The magnitude of the effect is small, with each extra $10,000 of income associated with, at most, only 0.7 percentage points higher leverage. Increased income appears to be more closely associated with higher values of both debt and housing assets than with the ratio of those two variables. We also find tentative evidence that the effect of household income on leverage is non-linear, with the negative sign on the income-squared variable implying that leverage is increasing in income but at a decreasing rate. The coefficient on this term is so small that leverage does not begin falling until income reaches about $500,000.
Two measures of households' subjective views about their incomes – the ease with which they are making ends meet (income adequacy), and their satisfaction with their pay – were included in the model to determine whether such measures of income relative to perceived requirements add information above that of measured income. Neither variable is closely correlated with reported actual income. Reported satisfaction with pay is statistically significant with a small positive coefficient, perhaps indicating that respondents that are highly satisfied with their pay are less concerned about their vulnerability to future income shocks, and are thus more willing to take on higher gearing.[7]
Past loan repayments in excess of the contracted minimum will naturally result in lower leverage at a given point in time, all else equal. Although the HILDA Survey does not explicitly ask about the extent of these past overpayments, respondents were asked if the loan repayments were (currently) ahead of schedule, behind schedule, or about on schedule. Households that reported that they were ahead of schedule in the repayments on the main loan against their home had leverage 5.4 percentage points lower than that of otherwise similar households.
The means of the household captures more than just its income. Factors such as family breakdown, permanency of employment, negative income shocks and familial support could also influence leverage by affecting households' ability to take on and pay off debt. Our results suggest that such factors do add some information in explaining household housing leverage. For example, households with separated household heads have considerably higher leverage (11 percentage points) than other households. However, the fact that divorced household heads do not have higher leverage than other households suggests the impact of family breakdown on leverage may be only temporary; this possibility could be confirmed using the longitudinal aspects of the HILDA Survey to track households through the process of breakdown.
One indicator of household means, although not a causal factor, is that the results show that households whose homes are in poor condition have higher leverage than other households. This may be an example of reverse causation; households with high leverage may be too financially stretched to pay for renovations, and might be unable to borrow more to do so.
4.2.3 Household characteristics and attitudes
Besides the structural characteristics of households such as age and income, we also expect household attitudes to housing and debt to influence their housing leverage. For example, we may have expected that households that are more comfortable about taking on debt would have higher leverage than other households. However, a variable that summarised households' attitude to borrowing for items such as holidays, cars, and clothes, did not enter significantly into the model, although the point estimate did have the expected sign. Similarly, risk-averse households might be expected to prefer to pay housing debt off more rapidly and thus have lower leverage. However, our results indicated that households indicating a high aversion to risk in their saving decisions did not have significantly lower leverage on their homes, although the coefficient on this variable is again of the expected sign. This may suggest that these households' aversion to the riskiness of debt might be offset by a preference for housing assets over other assets they perceive as riskier; confirming this suspicion will not be possible until Wave 2 data on other kinds of assets and debt are available.
Other attitudinal variables do, however, enter the regression significantly. For example, households that pay their credit card off on time each month have lower leverage than households that do not. This could reflect either such households' preference for paying as little interest as possible on their debt, or perhaps greater financial sophistication and means. Households with long savings horizons have slightly higher leverage than households with shorter savings horizons.
The results also show that several other indicators of households' financial situation have significant associations with leverage outcomes. Although some of these indicators are symptomatic of the same causes as are influencing leverage, rather than themselves being causal factors, they provide some descriptive value in determining what kinds of households are most leveraged. For example, households who have owned more than one home – as opposed to first-home buyers – have slightly higher than average leverage, which suggests that households take on more debt when trading up, relative to the asset's value. Households that report some rental income, and therefore must own investment property, also have substantially higher leverage (14 percentage points) than other households. This result probably identifies a sub-group of the population that has actively engaged in leveraged asset accumulation, and is therefore willingly taking on the increased financial risks that this entails.
We also observe that households that took out loans from financial institutions at the time of purchase have higher leverage than the small proportion that did not.[8] Households that did not require a loan from a bank or other financial intermediary presumably acquired the property through inheritance, or used their own resources and bequests, gifts or loans from friends and family to fund their purchase. Loans from friends and family are included in the measure of leverage used here, but the other means of funding the purchase are clearly substitutes for debt that would reduce initial leverage at the time of purchase. Although some of these households might subsequently take out a loan secured against their home, in general they are likely to have little debt against their home.
People's cultural background may affect their leverage by influencing attitudes to debt, homeownership and intergenerational transfers; variations in homeownership rates amongst households of different ethnic origins have previously been observed in Australian data (Bourassa 1994, 1995). To test whether these differences reflect the migration experience or transmitted cultural values, we included variables representing the country of birth of both the household heads and their parents. Migrants will report both their own and their parents' birthplaces as being outside Australia, while second-generation Australians will report parental birthplaces outside Australia and their own birthplace as Australia.
We found that only the parental background variables were significant. Households with heads whose fathers were born in continental Europe had leverage 7 percentage points lower than households where the head's father was born in Australia. In contrast, households with heads whose fathers were born in the UK had higher leverage than other households.[9] Taken at face value, these results could be interpreted as indicating that a combination of cultural values and intergenerational transfers explains the pattern of lower than average leverage for the children of European migrants, rather than being a product of the migration experience.
4.2.4 Geographic variables
We also include a series of regional dummies to potentially capture two effects. First, they may capture different preferences for leverage across different regions, or differences in lending policies of banks. Second, they may proxy for different rates of housing price growth across regions, which can be expected to have exogenously influenced households' housing leverage. Although disaggregated data on growth in median house prices over the past two years resulted in the expected significant negative coefficient on its own, this was dominated by the inclusion of a suite of location dummies distinguishing the inner suburbs of the capital city, the outer suburbs of the capital city, and the non-metropolitan regions of each state.[10] Households move at different times and have thus experienced different degrees of inflation of the value of their home since they purchased it. Available data on Australian housing prices do not permit construction of regional level data on housing price growth over each individual household's holding period for their home, so housing price growth had to be calculated over a fixed window. The dummies may therefore be capturing variations in averages for both price growth and holding period, as well as other regional influences on leverage.
Using inner Melbourne as our base category because it is the region that has experienced the most rapid price growth in recent years, we can see that all other regions have higher leverage than inner Melbourne, and that the differences are broadly consistent with the recent pattern of relative growth rates for housing prices. In general, leverage is higher in non-metropolitan regions than metropolitan regions, and leverage is highest in Tasmania and Queensland. Brisbane's high average leverage is a puzzle, given that its price growth has been rapid in recent years, but this may be partly a base effect.
4.2.5 Effect of selection bias
The model with selection effects shown in Table 4 provides only a marginal improvement in fit over a model estimated over only those households that have leverage (adjusted R2 of 0.278 versus 0.274). The coefficient on the tenure selection term is not significant, while the coefficient on the mortgage selection term is significant only at the 11 per cent level and not at more conventional thresholds. Given the non-overlapping sets of explanators in the selection equations, it seems unlikely that identification problems drive this result, although multicollinearity could be an issue instead. It is more likely that the opposite effects that key variables, such as age and time the household has lived at the address, have on mortgage and tenure selection partially net out in the leverage equation. Since the selection terms combine information from both selection equations, these important variables may generate little net selection bias. Together with the bias arising from other variables in the model, this seems to result in only a minor degree of selection bias even though this is clearly a model with self-selection. The difference between the bias-corrected marginal effects and total effects are consistent with the mortgage equation dominating the tenure equation when variables counteract each other.
Despite the insignificance of the selection terms, the effects of the adjustment on coefficients for several key behavioural variables relating to life cycle and tenure characteristics are nonetheless large enough to conclude that this exercise enhances our understanding of population behaviour compared with the results implied by the non-bias adjusted model. Table 5 presents selected coefficients from the unadjusted model alongside the comparable marginal effects derived from the model results shown in Table 4. This enables a comparison with the model with selection effects and thus demonstrates where there are important differences.
| With correction | Without correction | % difference | |
|---|---|---|---|
| Household income | 0.04 | 0.03 | 35.3 |
| Age | −0.48 | −0.36*** | 25.2 |
| Has rental income | 14.20*** | 14.10*** | 0.5 |
| Satisfaction with pay | 0.76*** | 0.75*** | 1.5 |
| Took out institutional loan to buy home | 12.60 | −1.30*** | 108.1 |
| Retired | −10.50 | −4.50 | 57.0 |
| Income adequacy | −0.70 | −0.10 | 85.3 |
| Married | 3.16 | 2.30 | 27.1 |
| Separated | 11.00*** | 10.20*** | 7.1 |
| Time lived at address | −0.75** | −0.44*** | 41.8 |
| Father born in Europe | −6.88*** | −6.90** | −0.34 |
| Moves in last 10 years | 0.84 | 0.99** | −19.13 |
|
Note: ***, **, and * represent significance at 1, 5 and 10 per cent levels. |
|||
The unadjusted model suggests a much smaller effect of age and time at address in diminishing the remaining loan size, and thus leverage, than the marginal effect implied by the model adjusted for selection bias. This unadjusted model also substantially understates the base effect of whether the household originally took out an institutional loan to help fund the purchase. Although neither specification generates an income effect that is significant at conventional levels, the point estimates are sufficiently different that economic interpretation might be affected.
In addition, our results suggest that this double-selection model is superior to a standard single-selection model with a Heckman correction. An alternative specification with only one selection equation, distinguishing mortgage-holders from other households and treating renters and homeowners without mortgages the same, produces different results that appear to fit the data less well than our preferred specification (these results are available from the authors). Although the measure of selection bias is not quite statistically significant, the results presented in this paper clearly show that such adjustments are useful when examining leverage across the whole household sector.
Footnotes
In an uncorrected model, the marginal effects only apply to those that actually have mortgages, while the bias-corrected (or population) marginal effects apply to all households if they were to have mortgages. The derived ‘population’ marginal effects are thus still conditional on the household having a mortgage. [6]
The point estimates of other parameters are not sensitive to the inclusion of these subjective means variables, indicating that their possible endogeneity is not a major concern. [7]
Only 4 per cent of households who report having a mortgage did not take out an institutional loan at the time of purchase. However, over all owners, this increases to 28 per cent. [8]
Using birthplace of mother or of either parent gave virtually identical results. The number of households where the heads or their parents were born in other regions was too small to produce statistically significant estimates. Variables representing birth in other regions were therefore excluded from our preferred specification. [9]
The housing price data used were a combination of regional-level median housing prices from Residex for the eastern seaboard states, and metropolitan and non-metropolitan dwelling prices compiled by the Commonwealth Bank for the HIA Housing Report for the other states. [10]