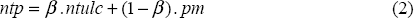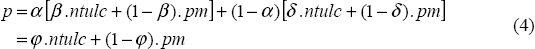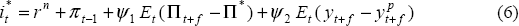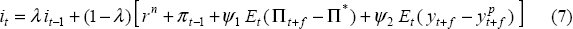RDP 2000-06: Inflation Targeting and Exchange Rate Fluctuations in Australia 2. Open Economy Inflation Targeting

In an open economy, a depreciation of the exchange rate affects inflation directly by increasing the domestic-currency price of imports, and indirectly by increasing foreign demand for domestic output. This exchange rate effect works in conjunction with the aggregate demand channel of monetary policy whereby a decrease in interest rates stimulates aggregate demand and increases inflation. Because monetary policy generally affects inflation more quickly through the exchange rate channel than through the aggregate demand channel, an opportunity arises for activist policy to use the direct exchange rate channel to control inflation at a short horizon. Such a policy of frequent interest rate adjustments, however, could induce considerable variability in other key macroeconomic variables.

Recognising these considerations, several recent papers have examined the issue of what is the most appropriate measure of inflation to target in a small open economy. Building on the work of Ball (1998) and Svensson (1998), Bharucha and Kent (1998) compared the implications of targeting aggregate and non-tradeable inflation in a simple theoretical model of a small open economy with tradeable and non-tradeable sectors (roughly calibrated, where possible, to match the Australian economy). Importantly, the model assumed that aggregate inflation was more susceptible to exchange rate fluctuations than was non-tradeable inflation.

Bharucha and Kent showed that the implications of aggregate and non-tradeable inflation targeting depended on the relative size and source of shocks hitting the economy. For exchange rate shocks, optimal monetary policy was more activist under aggregate inflation targeting. This reduced the volatility of the exchange rate and aggregate inflation, but increased the volatility of the interest rate, output and non-tradeable inflation. In comparison, the less activist optimal policy response under non-tradeable inflation targeting generated less variability in output and non-tradeable inflation, but increased the variability of the exchange rate and aggregate inflation.

Compared with exchange rate shocks, the monetary policy implications of aggregate and non-tradeable inflation targeting under demand and supply shocks were reversed – optimal policy under aggregate inflation targeting was less activist than non-tradeable inflation targeting.

In a more realistic setting with all shocks operating at once, the unconditional variances of all variables (except non-tradeable inflation) were higher under non-tradeable inflation targeting. The authors acknowledge, however, that this result depends on the arbitrarily chosen size of exchange rate shocks relative to demand and supply shocks.

In concluding, Bharucha and Kent were ‘unable to provide an answer as to whether aggregate inflation targeting [was] strictly preferable to non-traded inflation targeting’. Instead, they suggested that policy should be conducted with a medium-term perspective so as to avoid the undesirable outcomes associated with either inflation-targeting regime.

In this paper we take up the issue of open economy inflation targeting once more. However, our approach differs from Bharucha and Kent (and earlier papers) in two important ways.

Whereas most previous papers have addressed the issue using small theoretical models (sometimes calibrated to match a small open economy), we examine the issue in the context of an econometrically estimated model of the Australian economy. In this way, we hope that the results will be more relevant than those contained in the earlier studies.

Another significant departure from previous papers is our use of simple monetary policy rules (reaction functions) to determine interest rates rather than the optimisation of an explicit policy objective function. A number of recent papers have examined the properties of simple monetary policy rules and shown that they provide a fairly accurate characterisation of actual policy in most industrialised countries. Characterising monetary policy as following an interest rate rule provides us with a convenient means of changing the measure of inflation which policy responds to and allows us to examine a number of related issues, such as the optimal length of the policy forecast horizon.

2.1 The Distinction Between Aggregate and Non-tradeable Inflation

In his work on open-economy inflation targeting, Svensson (1998) explored the distinction between CPI-inflation targeting and targeting inflation of domestically produced goods (‘domestic-inflation targeting’). This distinction relies on the assumption that the country is small in the market for its imported goods, but large in the world market for its exportable output. The difference then between CPI-inflation and domestic-inflation reflects movements in the prices of imports which are determined by world prices and the exchange rate.

For Australia, we believe that the distinction between CPI-inflation and domestic-inflation is less appropriate for two reasons.

First, the prices of imported items in the Australian CPI are affected by more than just world prices and the exchange rate. Dwyer and Lam (1994), for example, found that the long run pass-through of exchange rate changes to the imported component of the Australian CPI was only about two-thirds. They argued that this reflected the costs, mainly incurred in the non-tradeable sector (for example, transportation, storage and wholesaling), of bringing imported goods to the retail market. A variable retail mark-up also contributes to the relative stability of imported goods prices in the face of exchange rate movements, and this too is a domestic consideration.

Second, the prices of import-competing and exportable goods in Australia are at least partly determined in world markets (Dwyer, Kent and Pease 1994). Australia's openness to international trade means that the prices of our import-competing goods are influenced by world markets. For example, the prices of domestically produced motor vehicles fell during 1998, at least partly in response to falls in the prices of imported motor vehicles. As for Australia's exportables, our small size and the homogeneity of many of our biggest exports means that we are more likely to be price takers on world markets. In any case, if we exclude imported and import-competing items (at a moderate level of aggregation in the CPI) from a definition of domestic inflation, we would also automatically exclude exportables.

Following Bharucha and Kent (1998), we argue that the appropriate distinction for a small open economy is between aggregate inflation and inflation in the non-tradeable sector.^[2] We formalise this distinction as follows.

Assume that the aggregate consumer price level (p) is a composite index of the prices of tradeable (tp) and non-tradeable goods (ntp):

where α represents the share of non-tradeable goods in the aggregate consumer price index.

Next, assume that non-tradeable prices are determined as a mark-up over the costs of production – domestic and imported costs. Domestic costs are mainly for labour and are represented by unit labour costs in the non-tradeable sector (ntulc – nominal wages adjusted for labour productivity in the non-tradeable sector). Imported costs reflect the prices of imported intermediate inputs, which we assume to follow the prices of final consumption imports (pm). Ignoring the mark-up, non-tradeable prices are given by:

Tradeable prices include the prices of wholly imported and import-competing final consumption goods (importables) and exportable consumption goods. Assume that importable prices mainly comprise the prices of imported final goods and intermediate inputs (pm), but are also affected by the labour costs, incurred in the non-tradeable sector, of bringing those goods to the retail market (ntulc). Exportable prices are determined by world prices (proxied by pm), with some adjustment also for non-tradeable sector labour costs. Tradeable prices are then given by:

Substituting (2) and (3) into (1), we arrive at the following expression for aggregate prices:

Furthermore, if β > δ, then φ < β. This implies that a given movement in the price of imports (bought about by a change in the exchange rate, for example) will have a greater effect on aggregate prices than non-tradeable prices. Econometric estimates of aggregate and non-tradeable inflation equations for Australia (see Appendix A and the discussion in Section 3) confirm this pattern of long-run elasticities.

Aggregate inflation, which incorporates the prices of tradeable goods, will be more susceptible to movements in the exchange rate than non-tradeable inflation. Because of this distinction, we later explore the implications of following policy rules which respond to each of these measures of inflation. Going a step further, we also examine rules in which the interest rate responds to movements in non-tradeable sector unit labour costs – a variable which is even less affected by exchange rate movements than non-tradeable inflation.

2.2 Monetary Policy Rules

In this paper we assume that monetary policy follows a linear interest-rate rule of the following general form:

where

This rule assumes the partial adjustment of the nominal interest rate (i) to a target rate (i^*), where the parameter λ (0 ≤ λ ≤ 1) represents the degree of interest rate smoothing. The target rate is a function of the deviation of year-ended inflation from target (Π − Π^*) and the output gap (y − y^p). When both of these feedback variables are zero then the target rate will be equal to the neutral real interest rate (rⁿ) plus expected inflation, proxied in our model by lagged aggregate inflation (π_t−1. Note that this represents the public – not the central bank – expectation for inflation.

The parameters ψ₁ and ψ₂ are reaction weights which measure the responsiveness of the target rate to each feedback variable, f is the forecast horizon (in quarters) at which the feedback variables enter the rule and E_t denotes the expectation of a variable formed at time t (conditional on the application of the policy rule through time).

Substituting (6) into (5) gives the following general rule:

It is worth highlighting a number of characteristics of this policy rule.

The rule is an example of a ‘simple’ monetary policy rule in the sense that it includes only two feedback variables – the deviation of inflation from target and the output gap. In this paper we restrict ourselves to this class of simple rules rather than more complex ‘optimal’ rules which can be derived by optimising an explicit objective function subject to the constraints implied by the equations in a model. There are a number of reasons for this. First, simple rules, particularly when they include forecasts of the feedback variables (f ≥ 0), can generally stabilise inflation and output almost as well as optimal rules while still satisfying their original purpose – to provide a simple and transparent guidepost for policy. Second, optimal rules, which are complex functions of all of the predetermined state variables in a model, are not as robust across model specifications as simple rules (Taylor 1999).^[3] Finally, simple rules provide us with a relatively straightforward means of experimenting with different aspects of the monetary policy operating framework – such as changing the measure of inflation which policy responds to and gauging the optimal forecast horizon for policy.

The variable Π can refer to a variety of inflation measures, not just aggregate inflation. This enables us to compare the implications of following policy rules which respond to different measures of inflation. Irrespective of the inflation measure used, the steady state assumptions of our model (discussed in Section 3.2) imply the same numerical inflation target (Π^* = 2½ per cent per annum).

In this paper we consider rules in which f lies in the range −1 to 8. When f = −1, policy responds to the most recently observed data – we call these ‘backward-looking’ rules. These rules, of which the Taylor (1993) rule is a prominent example, are only able to stabilise the economy if inflation and the output gap are quite persistent, so that their past values help predict future inflation. While these rules tend to perform quite well in closed economies, recent research has made it clear that policy-makers in open economies can stabilise the economy further by reacting to forecasts of the feedback variables rather than their lagged values (f ≥ 0 – which we call ‘forward-looking’ policy rules). In this way policy uses all available information to forecast the feedback variables (rather than just lagged values) and is better able to control for lags in the monetary policy transmission process. Forward-looking policy rules also correspond more closely with actual ‘pre-emptive’ policy-making. In our forward-looking policy rules, forecasts of the feedback variables are fully model consistent – that is, they are generated assuming that the central bank actively uses the same policy rule in each future period.

Note that we generally restrict ourselves to rules in which λ = 0 (no interest rate smoothing). However, in the context of discussing possible remedies to excessive interest rate variability (in Section 4.1), we investigate rules in which λ > 0 and rules in which λ = 0 with constrained interest rate variability.^[4]

Footnotes

In any case, the Australian Bureau of Statistics has recently ceased recording the distinction, except for motor vehicles, between the domestic and imported components of the CPI, choosing instead to report only the distinction between tradeable and non-tradeable components. Moreover, the price deflators in the national accounts do not provide a good proxy for the domestic component of the CPI. [2]

This argument may not be as relevant for simple rules which include forecasts of the feedback variables because these forecasts (model consistent or otherwise) are complex functions of the entire model. [3]

A more rigorous approach, beyond the scope of this paper, which addresses the various forms of uncertainty which face policy-makers in practice, is also discussed briefly in Section 4.1. [4]