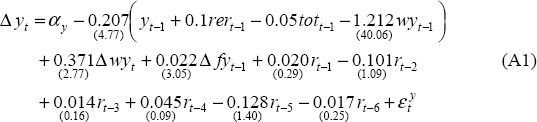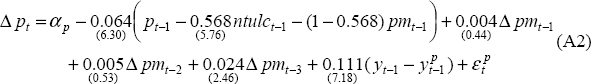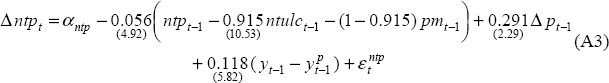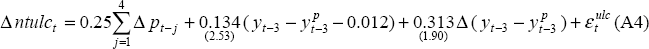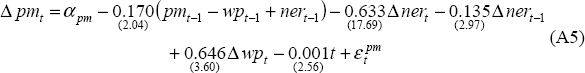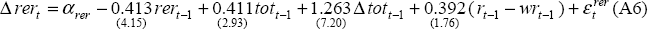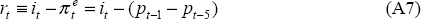RDP 2000-06: Inflation Targeting and Exchange Rate Fluctuations in Australia Appendix A: Estimates of the Model

The model which we use is a modification of a small data-consistent set of equations developed in the course of previous research at the Reserve Bank of Australia. These equations were generally developed in isolation and first treated as a single macroeconomic model by de Brouwer and O'Regan (1997) for the purposes of stochastic simulations. A detailed description of a more recent version of the model is provided by Beechey et al (2000).

Most of the equations are expressed in error-correction form in order to distinguish the long-run relationships between the variables from their short-run dynamics. In each case, we began with general specifications (containing many lags of the dynamics) and arrived at a parsimonious specification using an informal general-to-specific model reduction approach. Various parameter restrictions were tested and imposed – in accordance with our theoretical priors – in an effort to include as much theoretical content as possible while still adhering to the overriding principle of data consistency.

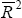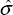Interest rates are expressed in per cent per annum divided by 100, and all other variables are expressed in logs. All data are quarterly and Δk denotes the quarterly log difference in variable k, is the adjusted squared multiple correlation coefficient, is the estimated standard error of the regression. Where appropriate, in the specification of the equations below, error-correction terms are contained within square brackets. The definition, measurement and source for each of the variables is contained in Appendix D.

Equations (A1) to (A6) list the specification and coefficient estimates (with associated absolute values of t-statistics in parentheses below) for each of the behavioural equations in the model. The two identities in the model are given by Equations (A7) and (A8). Section 3 of the main text contains a more general description of each of the equations.

Note, for the purposes of estimation, potential non-farm output (y^p) is equal to the linear trend of actual non-farm output (y) generated over the sample period: 1980:Q1–1998:Q4.

Non-farm output equation

Sample: 1982:Q1 – 1998:Q4 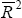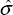DW = 2.116

When freely estimated, the coefficients on the real exchange rate (rer) and the terms of trade (tot) in the error-correction term, while of the correct sign, were insignificantly different from zero. Nevertheless, we have reason to believe that these variables have a significant, albeit small, effect on output. In order to account for this, the long-run elasticities on these two variables were calibrated to accord more closely with our priors while still being accepted by the data (χ² (2) = 1.694 [0.43]). According to this calibration, the direct effect of a terms of trade shock on output is small. Moreover, the resulting exchange rate movement's effect on output more than offsets the terms of trade effect, so a positive terms of trade shock eventually has a negative effect on output.

The six lags of the real interest rate are jointly significant (χ² (6) = 18.000 [0.01]) and their sum implies that a sustained one percentage point increase in the real cash rate eventually reduces the level of output by 0.81 per cent.

Aggregate price inflation equation

Sample: 1984:Q1 – 1998:Q4 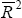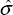DW = 1.669

The restriction of static homogeneity was accepted by the data (χ² (1) = 0.908 [0.34]) and imposed.

Non-tradeable price inflation equation

Sample: 1984:Q1 – 1998:Q4 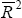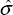DW = 2.308

The restriction of static homogeneity was accepted by the data (χ² (1) = 0.185 [0.67]) and imposed.

Non-tradeable unit labour cost equation

Sample: 1984:Q1 – 1998:Q4 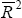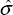DW = 1.919

The restriction that the coefficients on lagged inflation sum to one (the property which underlies a vertical long-run Phillips curve) was accepted by the data (χ² (1) = 2.265 [0.13]) and imposed. The restriction that each of the coefficients on lagged inflation is equal to 0.25 was not accepted by the data, but was imposed in order to avoid an implausible dynamic response of non-tradeable unit labour costs to a change in aggregate prices.

In estimating the unit labour cost equation, the level of the output gap was adjusted downwards by 1.2 per cent in order to roughly capture the observed disinflation which actually occurred over the estimation sample period.

Import price equation

Sample: 1982:Q1–1998:Q4 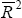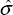DW = 2.189

The restriction of static homogeneity (purchasing power parity in the long-run) was accepted by the data (χ² (2) = 1.175 [0.56]) and imposed.

The time trend (t) in this equation reflects a gradual shift in the source of Australia's imports towards lower priced trading partners in the Asian region, suggesting that our measure of world prices (wp) does not fully capture the foreign-currency price of all of our imports. In simulations of the model, the coefficient on this time trend is set equal to zero.

Real exchange rate equation

Sample: 1985:Q1 – 1998:Q4 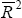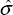DW = 1.743

Real interest rate identity

Nominal exchange rate identity

For the simulations, the constant term in each equation was calibrated to place the model in equilibrium in the initial period (α_y = −3.354, α_p = 0.006, α_ntp = 0.004, α_pm = 16.998 and α_rer = 0.144) for initial values for each variable (other than interest rates) of 100.