RDP 2000-06: Inflation Targeting and Exchange Rate Fluctuations in Australia 3. The Model

The model we use in this paper comprises six econometrically estimated equations for aggregate output (real non-farm GDP), inflation (that is, equations for aggregate and non-tradeable inflation, non-tradeable unit labour costs and import prices) and the real exchange rate. There are also two identities; for the real interest rate and the nominal exchange rate. In the following section we provide a brief description of each equation. Empirical estimates of the equations are contained in Appendix A.

3.1 Summary of the Model's Equations

The demand side of the model is captured by an aggregate demand curve which models real non-farm output as depending on past real interest rates, real foreign output – proxied by US GDP – the real trade-weighted exchange rate and the terms of trade. The equation also allows for the dynamic impact of farm output on non-farm output. Estimates of the equation imply that a sustained one percentage point increase in the real interest rate eventually causes a 0.81 percentage point cumulative detraction from the level of output. When the real interest rate returns to its policy-neutral level – which we set at 3½ per cent – output eventually returns to its long-run path, implying that monetary policy has no permanent effect on the level of real output.

Following on from the discussion in Section 2.1, we model both aggregate and non-tradeable underlying inflation as mark-ups over costs, domestic and imported.^[5] Domestic costs are represented by unit labour costs in the non-tradeable sector while imported costs are represented by import prices. As expected, the relative importance of import prices is found to be much lower in the non-tradeable inflation equation because in that equation import prices reflect only the costs of imported intermediate inputs. The presence of import prices in the aggregate inflation equation reflects the cost of both imported intermediate inputs and the direct effect of imported final consumption goods prices. In each case, the retail mark-up on costs is also affected in the short run by an output gap – the difference between actual and potential output – which captures the changing mark-up over the cycle.

Nominal unit labour costs in the non-tradeable sector are modelled as a Phillips curve relationship, being determined by expected inflation and the lagged level of excess labour demand, proxied by the output gap. The use of an aggregate output gap (rather than an output gap for the non-tradeable sector) reflects our assumption that labour flows freely between the two sectors. A ‘speed-limit’ term (the lagged change in the output gap) is also included, consistent with previous evidence for Australia.^[6]

Expected inflation is proxied by average past aggregate inflation. Our appeal, as always, was to data consistency, which, for Australia, generally does not sit favourably with rational (forward-looking) inflation expectations.^[7] Note that backward-looking expectations also generate greater persistence in the response of inflation to shocks than does rational expectations, implying greater variability in output and inflation than otherwise for the results presented in Section 4.

The use of aggregate inflation for measuring inflation expectations assumes significant wage bargaining power on the part of employees who are concerned with maintaining their real consumption wage. We return to the assumptions regarding the role of aggregate inflation and output in the determination of unit labour costs in Section 4.

The sum of the coefficients on lagged inflation was restricted to equal one, implying that the unit labour cost Phillips curve is vertical in the long run and that all shocks to inflation are permanent since they feed through entirely to unit labour costs and, hence, back into prices (the coefficients on lagged inflation are also restricted to be equal to each other in order to avoid an implausibly volatile response of nominal unit labour costs to changes in prices).

Following Dwyer et al (1994), the domestic-currency (‘over-the-docks’) price of imports is determined by world prices converted to domestic currency using a nominal effective (G7 GNP-weighted) exchange rate. Dynamics are included to reflect the differing speeds of pass-through of changes in world prices and the exchange rate. Long-run pass-through is found to be complete.

The real effective (trade-weighted) exchange rate is modelled as having two ‘fundamental’ determinants: the terms of trade and the short-term real interest-rate differential between Australia and the rest of the world. A standard, forward-looking international interest-rate arbitrage condition is conspicuous in its absence but has repeatedly failed to replicate the observed behaviour of the Australian dollar. Instead, a lagged real interest-rate differential has consistently proved more successful (see, for example, Blundell-Wignall, Fahrer and Heath (1993) and Tarditi (1996)). Given that the link between the exchange rate and monetary policy is important to the central issue addressed by this paper, we later experiment with modifications to this relationship.

Although empirically the nominal G7 GNP-weighted exchange rate works best for estimating import prices in Australia, while the real trade-weighted exchange rate works best for estimating Australian output, we treat them as equivalent in the simulations. That is, we define changes in the nominal exchange rate as being equal to changes in the real exchange rate adjusted for the domestic–foreign inflation differential. This also facilitates a link between the real interest rate and domestic inflation via the nominal exchange rate.

The real interest rate is defined as being equal to the nominal interest rate less expected inflation, which we assume to be equal to lagged aggregate inflation.

For the purposes of the stochastic simulations, the exogenous variables in the model (foreign output, terms of trade, farm output, world prices and the world short-term real interest rate) were modelled using simple trend-correcting or autoregressive mechanisms. Appendix B contains the empirical estimates of each of these equations.

The final piece of the model concerns the determination of the nominal interest rate (the monetary policy instrument). As we discussed earlier, our approach is to model monetary policy as following an explicit monetary policy rule. Equation (7) showed the general form of the monetary policy rules which we use in this paper. In Section 4 we show the results of simulating the model under different specifications (and parameterisations) of this monetary-policy rule. Comparing the variability of the simulated outcomes for aggregate inflation and the output gap (and the other endogenous variables) then allows us to determine which rules are preferable.

3.2 Steady State of the Model

The steady state of the model relies upon our arbitrary prescription of a neutral (equilibrium) real interest rate of 3½ per cent. The difference between this and the long-term average of the world real interest rate can then be treated as a constant risk premium. Given steady farm output growth and a constant real interest rate and terms of trade (implying a constant real exchange rate), real equilibrium in this model is characterised by potential and actual output growing by around 3½ per cent per annum. See Appendices A and B for discussion on the measurement and simulation treatment of potential output.

The inflation target embedded in the monetary-policy rule acts as the nominal anchor and brings about nominal equilibrium in the model. This is characterised by domestic and foreign inflation and, because the output gap is closed in equilibrium, unit labour costs all growing at 2½ per cent per annum. The equilibrium nominal interest rate is 6 per cent.

If productivity in the tradeable sector is higher than productivity in the non-tradeable sector but wages growth is the same, non-tradeable price inflation will be higher than aggregate price inflation in equilibrium.^[8] Import price inflation, in turn, will be lower than aggregate price inflation, reflecting the lower prices of higher-productivity tradeable goods that we import. However, for simplicity, we assume that all prices (domestic and foreign) and unit labour costs grow at the same rate in the steady state. While unrealistic, this assumption is likely to have only minor implications for the model's dynamic properties which are the focus of our attention.

3.3 Transmission Channels of Monetary Policy in the Model

Despite its simplicity, the model still captures the two usual channels of monetary-policy transmission in an open economy.

First, there is a conventional ‘aggregate demand’ channel, whereby real interest rates affect output – implicitly investment and other interest-sensitive components of output – with a lag. The output gap then affects price inflation directly, by changing the size of the mark-up in the two price equations, and indirectly, through the unit labour cost Phillips curve equation. Associated with this, there is an ‘expectations’ channel. With backward-looking inflation expectations, any change in monetary policy which influences actual inflation will also change inflation expectations which, in turn, affects wages and then prices. Second, monetary policy affects the exchange rate, which in turn affects inflation directly, by changing the domestic-currency price of imports, and indirectly, by changing the relative demand for foreign and domestic output.

The relative timing of the effect of monetary policy through each of these channels is consistent with most other open-economy models. An increase in interest rates takes two periods to reduce aggregate inflation through the exchange-rate channel – one period to affect the exchange rate and a further period for the exchange rate to affect prices. In contrast, an increase in the interest rate takes three periods to reduce inflation through the aggregate demand channel – two periods to reduce output and a further period for output to affect prices. Non-tradeable inflation, which excludes movements in the prices of imported final consumption goods, is less sensitive to the direct exchange rate channel.

3.4 Summarising the Model's Dynamic Properties

In order to preview the model's dynamic properties, we generated the dynamic impulse response of each of the endogenous variables to a once-off depreciation in the level of the real exchange rate of 10 per cent. All other shocks, including subsequent shocks to the exchange rate, were set to zero for the entire simulation period.

For the purposes of this experiment, we also assumed that the parameters of the monetary-policy rule (Equation (7)) were f = 3, ψ₁ and ψ₂ = 3, λ = 0 and π = aggregate inflation. This particular choice of reaction coefficients yields outcomes that, though not on the efficient frontier of output and inflation variability derived from stochastic simulations of the model with the three-period-ahead forecast monetary-policy rule, generate fairly plausible variability in the nominal interest rate.

Figure 3 summarises the model's dynamic properties by tracing out the impulse response of each of the endogenous variables to the temporary exchange rate shock. The responses are measured as per cent deviations from baseline (steady-state) values. Inflation and growth in unit labour costs and import prices are measured as deviations from baseline in year-ended percentage change terms.

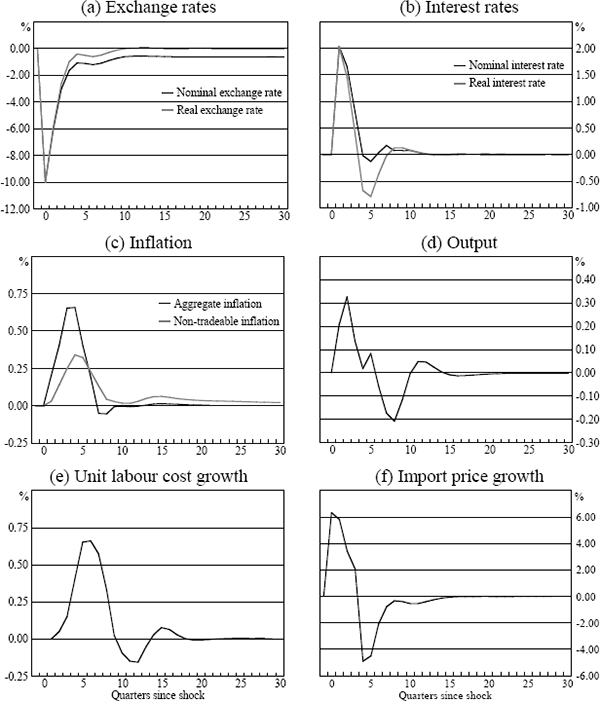
The real exchange rate shock coincides with an equal sized depreciation of the nominal exchange rate, which, via import prices, begins to drive up aggregate inflation almost immediately. The favourable relative price shift also encourages demand for net exports (assuming the terms of trade remains constant) which translates into higher output. Consistent with the policy rule, the nominal (and real) interest rate rises immediately, driven by higher inflation and output gap forecasts. This monetary policy tightening helps reverse the initial depreciation. Given the lags of monetary policy, though, the policy response does not start to have any significant impact on output and inflation until around three quarters into the simulation.

Panel (c) shows the different response of aggregate and non-tradeable inflation to the exchange rate shock. The exchange rate depreciation feeds into aggregate inflation much sooner. This reflects the impact of the exchange rate on the prices of imported final consumption goods and services, an effect excluded from non-tradeable inflation. The exchange rate depreciation does eventually show up in non-tradeable inflation, but the peak is lower than for aggregate inflation. Ultimately, the policy response brings both measures of inflation back to target. Aggregate inflation returns somewhat quicker owing to its higher long-run speed of adjustment coefficient.

Repeating this experiment with a monetary-policy rule that responds to the deviation of non-tradeable (rather than aggregate) inflation from target invokes a smaller initial policy response. This is seen in Figure 4, which compares impulse responses under the two different specifications of the monetary-policy rule. The response of non-tradeable inflation to the exchange rate shock was lower than the response of aggregate inflation, so the initial policy move under the non-tradeable inflation rule is smaller (Panel (b)). In this case, because policy does less to offset the stimulatory effect of the exchange rate depreciation on output (Panel (d)), the peak of the aggregate and non-tradeable inflation cycles is actually slightly higher under the non-tradeable inflation rule (Panel (c)). While the initial response is lower, policy under the non-tradeable inflation rule later remains tighter, for longer, in order to offset the higher inflation and output gap.

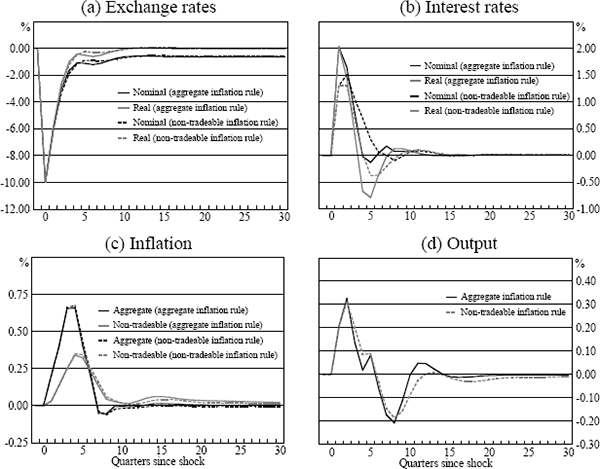
For a temporary exchange rate shock, the results in Figure 4 show that a monetary-policy rule in which the interest rate responds to non-tradeable inflation (rather than aggregate inflation) can actually induce greater conditional variability in output. Whether such a rule would reduce the unconditional variability of output in a stochastic simulation (where all shocks are operating) is the empirical issue addressed in the next section.

Footnotes

For the purposes of estimation, non-tradeable inflation was constructed by eliminating from the aggregate underlying CPI those sectoral components for which exports or import-competing production account for at least 10 per cent of total sectoral production. This disaggregation of the aggregate price series into tradeable and non-tradeable components follows the classification scheme originally used by Dwyer (1992). See Appendix A in Bharucha and Kent (1998) for further details on the measurement of non-tradeable inflation. [5]

The empirical fit of this unit labour cost equation is quite poor. Despite the importance of unit labour costs to inflation outcomes, the difficulty of modelling unit labour costs has, in the past, prompted attempts to develop models of inflation which exclude unit labour costs. One such empirically successful approach is to model price inflation directly in an expectations-augmented Phillips curve – ignoring unit labour costs completely. For example, see Gruen, Pagan and Thompson (1999). [6]

We experimented with forward-looking inflation expectations – derived, for example, from the difference between nominal and indexed (real) bond yields – but were unable to find a significant influence for them. Gruen, Pagan and Thompson (1999) estimated a low weight – around 10 per cent or less – on forward-looking inflation expectations in their more fully specified Phillips curve equations. [7]

Consistent with this, regressions of aggregate prices on aggregate unit labour costs (and other variables) generally find a significant role for a time trend. [8]