RDP 1999-10: The Implications of Uncertainty for Monetary Policy 4. Optimal Policy Ignoring Parameter Uncertainty

All of the estimated regression parameters in Table 1 are point estimates of the true parameter values and, as such, are random variables. The uncertainty surrounding these point estimates is partly reflected in their associated standard errors. This section highlights the consequences for monetary policy when the policy-maker assumes that these point estimates accurately describe the true economy. We generate a range of model-optimal policy responses and associated forecast profiles that would obtain under different draws of the parameter estimates from their underlying distribution. We describe these optimal policy responses as ‘naive’ because they ignore parameter uncertainty. In Section 6, we show how these policy responses can change when the optimal policy problem is solved recognising parameter uncertainty.

For each equation, we assume that the parameters are normally distributed with first moments given by their point estimates in Table 1 and second moments given by the appropriate entries in the estimated variance-covariance matrix of the parameter vector.^[6] Because each equation is estimated separately, there is no information available concerning the cross correlations between the parameters in the different equations. This implies that the variance-covariance matrix of the entire parameter vector is block diagonal, with each block given by the variance-covariance matrix of each individual equation.^[7]

While we characterise parameter uncertainty as being entirely caused by sampling error, this understates the variety of factors that can contribute to imprecision in the parameter estimates. When we estimate each of the five behavioural equations, we assume that the parameters do not change over time. Any changes in the parameters must then be partially reflected in the parameter variance-covariance matrix. This contribution to parameter uncertainty actually derives from model misspecification rather than sampling error.^[8] While we ignore these distinctions for the remainder of the paper, we acknowledge that the sampling error interpretation of the variance-covariance matrices may overstate the true sampling error problems and understate the problems of model misspecification and structural breaks in the model.

The remainder of this section presents forecasts that arise when the monetary authority faces a given parameter-estimate draw and believes that this draw represents reality, with no allowance made for uncertainty.^[9] By solving the optimal-policy problem for a large number of parameter draws, we obtain a range of forecasts which indicate the consequences of ignoring parameter uncertainty. Starting from the steady state defined in the previous section, we assume that the system is disturbed by a single one percentage point shock to one of the five estimated equations. Then, for one thousand different parameter draws, the naive optimal policy problem is solved to generate the path of the nominal cash rate and the corresponding forecast profiles over a ten-year horizon. Each of the simulations that follow are based on the same one thousand draws from the underlying parameter distribution.

For example, consider a one percentage point shock to real output. Figure 1 summarises the results of this simulation. In this figure, the maximum, minimum and median along with the first and third quartiles illustrate the dispersion of forecast profiles generated by the different parameter draws. The central black line denotes the median, while the limits of the light shaded regions are the maximum and minimum. The darker shaded region corresponds to the inter-quartile range.

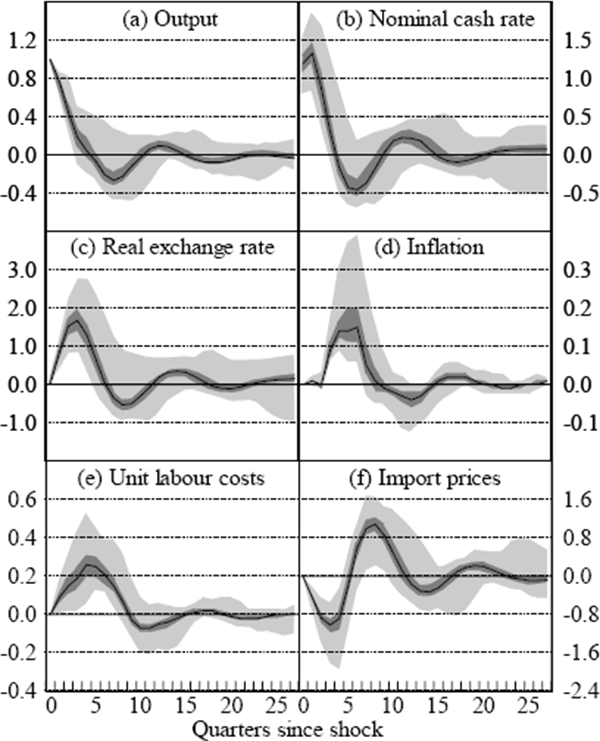
Note that the spread of forecasts around the median need not be symmetric. This is because asymmetries result from non-linearities in the way that the model parameters enter the construction of the forecasts. Although the model is linear in each of the variables, forecasts can be high-order polynomials in the lag coefficients.

To begin with, the output shock opens up a positive output gap which generates wage pressures in the economy. Feedback between wages and prices means that this wage pressure eventually feeds into price inflation. Consistent with the monetary authority's objectives, the optimal response to this shock is to initially raise the nominal cash rate. However, the size of this initial tightening can vary by up to three-quarters of a percentage point, depending on the parameter draw. With backward-looking inflation expectations, the rise in nominal interest rates raises the real cash rate, which has a dampening effect on output and eventually reverses the upward pressure on unit labour costs and inflation. The higher real interest rate also appreciates the real and nominal exchange rate, lowering inflation directly by reducing the Australian dollar price of imports and indirectly, by reducing output growth.

Over time, the initial tightening is reversed and eventually policy follows a dampening cycle as the output gap is gradually closed and wage and price inflation pressures subside. In the limit, all real variables and growth rates return to target and the system returns to the steady state.^[10]

What is most striking about these simulations is the range of different forecast profiles caused by parameter uncertainty. For example, depending on the parameter draw, the optimal policy response at any time during the forecast horizon can vary by as much as one and a half percentage points. This variation demonstrates that naive policy responses are not robust across parameter draws. Faced with the observed parameter uncertainty in this model (captured by the variance-covariance matrix), there is no way of knowing ex ante which parameter draw is closest to the true parameters of the economy, and therefore, there is scope for a wide margin of error following implementation of any one of these optimal policy responses.

It should be stressed that the optimal policy responses in Figure 1 assume no learning on the part of the monetary authority. Although the monetary authority may set interest rates according to a calculated optimal policy path, the economy will only ever evolve according to the true parameter draw. Generically, the forecasts of the monetary authority will be proved wrong ex-post, providing a signal that the initial parameter estimates were incorrect. If the monetary authority learns more about the true model parameters from this signal, then Brainard-type uncertainty will gradually become less relevant over time.^[11] However, in the naive policy responses shown in Figure 1, this type of learning is ruled out because we assume that the policy-maker always believes that the given parameter estimates are the true parameter values. In this case, any deviation between the actual and forecast behaviour of the economy would be attributed to unanticipated shocks.

We also examine the range of forecast profiles obtained under shocks to the other endogenous variables. Figure 2 shows the optimal response of the nominal cash rate to various other one percentage point shocks. These simulations are similar to that shown for the output shock in the sense that they all exhibit considerable variation in the optimal policy response across different parameter draws. However, in all cases, the optimal policy response drives the economy back into equilibrium with real variables trending back to their baseline values and nominal growth rates stabilising in accordance with the inflation target.

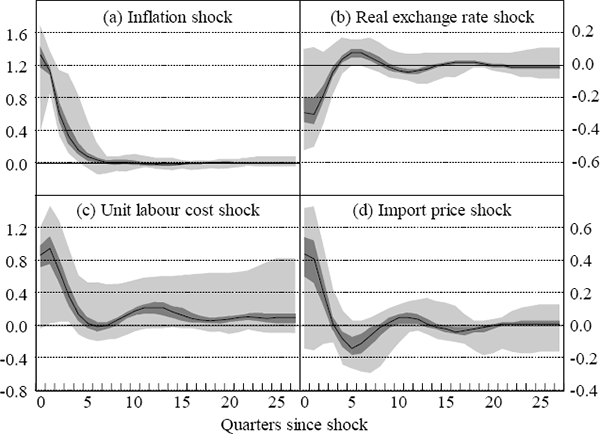
These simulations show that, where there is uncertainty regarding the true model parameters, the naive optimal policy response can vary quite considerably with observed parameter estimates. There are certainly considerable risks involved in implementing policy assuming that the estimated parameters are equal to their true values. In the next section, we demonstrate how the optimal policy problem can be modified to explicitly take into account parameter uncertainty. Rather than solving for the optimal path of the cash rate for a particular set of parameter estimates, the monetary authority takes into account the uncertainty associated with the distribution of parameter estimates and adjusts the policy response accordingly.

Footnotes

This approach to defining a distribution from which to draw the parameters of the model also ignores uncertainty about the estimates of the variance-covariance matrices themselves. Note also that the assumption that all parameter estimates are normally distributed is not correct. For example, the speed of adjustment parameters in each of the error-correction equations in Table 1 are actually distributed somewhere between a normal distribution and the Dickey-Fuller distribution (Kremers, Ericsson and Dolado 1992). This distinction is unlikely to make much difference to our results however, so for computational convenience, we have maintained the assumption that all of the parameters are normally distributed. [6]

For the real exchange rate and terms of trade parameters in the output equation, which have been calibrated, the appropriate terms in the variance-covariance matrix have been approximated by the corresponding terms in the variance-covariance matrix of the unconstrained (fully estimated) output equation. [7]

An alternate interpretation is that instead of the parameters being fixed, but just estimated with error, the parameters may in fact vary stochastically (and, in this case, from a multivariate normal distribution). With this interpretation, however, the distinction between model misspecification and sampling error becomes less clear. [8]

Each draw of the model parameters requires pre-multiplication of a vector of independent standard normal variates by the lower triangular Cholesky decomposition of the full variance-covariance matrix. [9]

While this is true for the model which we are using in this paper, after the 27 periods shown in Figure 1, some of the variables do not completely return to steady state. This is because the mean parameter draw results in a model which is quite persistent anyway and furthermore, some of the more extreme parameter draws can generate larger and more long-lasting cyclical behaviour in the variables. Eventually, however, all of the real variables and growth rates will return to steady state. [10]

Of course, the policy-maker will not be able to resolve uncertainty through time if the source of the ex-post forecasting error is parameter variation. [11]