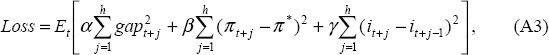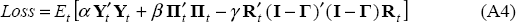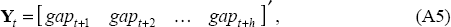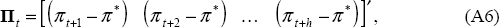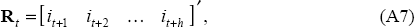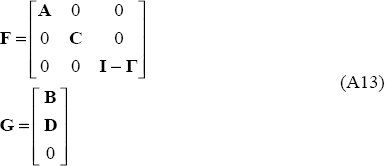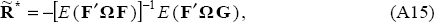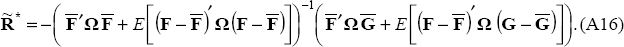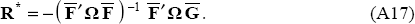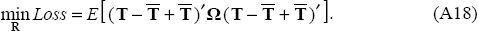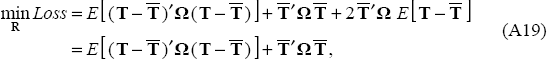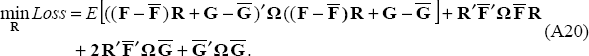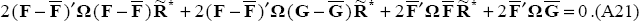RDP 1999-10: The Implications of Uncertainty for Monetary Policy Appendix A: Generalising the Optimal Policy Problem

In this appendix, we generalise Brainard's (1967) solution to the optimal policy problem for a monetary authority with quadratic preferences using a dynamic, multivariate model with stochastic parameter uncertainty.

To begin with, we show how the optimal policy problem for a monetary authority with quadratic preferences given by Equation (1) and a backward-looking multivariate model of the economy (that is linear in both the variables and the shocks) can be written in the following general form:

subject to:

To prove this, recall that the preferences of the monetary authority can be summarised by the following intertemporal quadratic loss function:

which can be rewritten using matrix notation as:

where:

Γ is the matrix that lags the nominal interest rate vector R_t by one period; and I is an (h×h) identity matrix. The subscript t denotes the current date from which forecasts are being generated.

Given that the model of the economy (Table 1) is linear, the policy target variables are affine transformations of the forecast profile for the policy instrument:

and

where A, B, C and D are stochastic matrices constructed from the parameters of the model and the history of the economy. The structure of these stochastic matrices is determined by the relationships laid out in the definition of the model's equations. Matrices B and D are the impulse response functions of the output gap and inflation to a shock at time t. Likewise, matrices A and C are the marginal impact of the nominal cash rate on the output gap and inflation respectively.

By defining Δ_t ≡ (I – Γ)R_t as the vector of first differences in the nominal cash rate over the forecast horizon, it is possible to specify the full set of policy targets as:

Then, upon dropping time subscripts, the optimal policy problem can be restated succinctly as:

subject to:

where the matrices F and G are defined in terms of A, B, C, D and (I – Γ) as:

and the weights on the different components of the loss function α, β and γ, have been subsumed into the diagonal matrix Ω according to:

where I is the same identity matrix used to define the first differences in the cash rates, Δ. Ignoring the fact that it is in matrix notation and observing that the target values of the target variables have been normalised to zero, this problem is exactly the same as that examined by Brainard (1967).

If F and G are stochastic, the solution to the optimal policy problem described by Equations (A1) and (A2) is:

which can also be expressed as:

Alternatively, if F and G are deterministic (with values 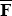and 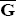), then the solution to the optimal policy problem is:

To show this, rewrite the loss function in Equation (A1) by adding and subtracting the expected values of T from it, yielding:

Upon expanding, this loss function can be also be expressed as:

taking advantage of the fact that .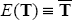

Substituting in Equation (A2) and simplifying then yields:

The first order necessary condition for this optimisation problem is obtained by differentiating with respect to R:

Solving for 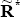then gives optimal policy when taking uncertainty into account, as expressed in Equations (A15) and (A16). Given that the loss function is strictly convex, this first order necessary condition is also sufficient for a minimum of the expected loss function.

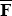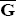The naive optimal policy response shown in Equation (A17) obtains as a simplification of Equation (A16) when F is set to and G is set to , that is, when F and G are deterministic.