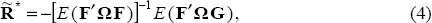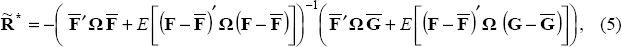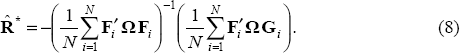RDP 1999-10: The Implications of Uncertainty for Monetary Policy 5. Characterising Parameter Uncertainty

The main contribution of this paper is to solve for optimal policy in the context of an empirical model of the Australian economy, taking into account parameter uncertainty. To achieve this, we first generalise the Brainard formulation of optimal policy under uncertainty to accommodate multivariate models and multiple-period time horizons. We then draw out the intuition of this formulation using a stylised example. In the following section, we apply this formulation to the more fully-specified empirical model described in Section 3 in order to examine some of the implications of parameter uncertainty for monetary policy.

Matrix notation makes the following generalisation of the optimal policy problem and its solution considerably more transparent. The generalisation is derived in more detail in Appendix A.

The optimal policy problem for a monetary authority with quadratic preferences given by Equation (1) and a backward-looking multivariate model of the economy (that is linear in both the variables and shocks) can be written in the following general form:

subject to:

where T is a vector of policy targets in each period of the forecast horizon; R is the vector of policy instruments; the matrices, F and G are functions of both history and the parameter estimates while Ω summarises the penalties contained in the objective function. The time subscript has been omitted for simplicity. This general form for the optimal policy problem highlights its similarity to the problem originally solved by Brainard. Because the loss function is quadratic and the constraint set is linear, the usual optimal policy response under parameter uncertainty will apply.

Specifically, if F and G are stochastic, then the solution to the optimal policy problem is:

which can also be expressed as:

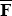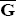where is the expectation of F and is the expectation of G.

Alternatively, if F and G are deterministic (with values 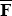and ), then the solution to the problem becomes:

F and G will be stochastic if they contain parameter estimates. Therefore, the solution described by Equations (4) and (5) corresponds to optimal policy acknowledging parameter uncertainty. The deterministic case in Equation (6) describes the naive policy response, when the monetary authority ignores parameter uncertainty. Comparing Equations (5) and (6), the difference between optimal policy responses with and without parameter uncertainty can be ascribed to the variance of F and the covariance between F and G. Brainard's policy conservatism result depends crucially on the independence of F and G. However, F and G will not be independent if they are derived from a model that exhibits persistence.

To make the optimal-policy definition in Equation (5) operational, it is necessary to compute the variance and covariance terms. This can be done using a sample estimate of the loss function in Equation (2):

where N is the number of parameter draws. This essentially computes the average loss over N parameter draws. The first-order necessary condition for this loss function to be minimised subject to the set of constraints in Equation (3) is then just the sample estimate of (4):

By averaging across a large number of parameter draws, optimal policy can be computed from the linear relationship between the target variables of policy and the policy instrument. As the number of draws from the estimated parameter distribution increases, this approximation will tend to the true optimal policy given by Equation (4). The naive policy response is computed by setting N = 1 and using the mean parameter draw to compute optimal policy from Equation (8). In this case, the mean parameter draw is interpreted as the ‘true’ model parameters, ignoring any uncertainty which we may have about them.

To illustrate the intuition behind these results, we first examine optimal policy responses in a stylised model which is an extension of the model considered by Brainard (1967). In the next section, we apply the generalised optimal policy solution to the model summarised in Table 1.

The original Brainard model assumed that the policy-maker minimised squared deviations of a variable y from a target (normalised to zero) by controlling a single policy instrument i, for an economy described by:

where θ is an unknown parameter representing the effectiveness of policy and ε is an independently and identically distributed white-noise process. To explore the issues involved in generalising this specification, it is useful to consider an economy that also includes a role for dynamics:

where ρ is another unknown parameter representing the degree of persistence in the economy.

In this model, parameter uncertainty arises when ρ and θ can only be imprecisely estimated. The central message of this section and the next is that the implications of parameter uncertainty depend crucially upon the relative uncertainty about policy effectiveness (θ) and persistence (ρ). If uncertainty about policy effectiveness dominates, then the usual Brainard conservatism result obtains. However, if uncertainty about persistence is more important, then optimal policy may be more aggressive.

The loss function is assumed to be the unweighted sum of squared deviations of the target variable y in the current and all future periods. For a given shock to the target variable, the optimal policy response is found by minimising this loss function. Assume that the two parameter estimates in Equation (10) are drawn from different independent normal distributions. For the uncertainty-aware optimal policy, we take one thousand draws from the underlying parameter distributions and compute the optimal policy response using the frequency sampling approach described by Equation (8). We then compare this with the naive optimal policy response which is computed using only the mean parameter draw.

To contrast the policy implications of each of these two types of uncertainty, we derive the optimal policy responses to a standardised shock under differing levels of relative uncertainty about each of the parameters. In what follows, we assume that there is a one unit shock to the target variable in the initial period (ε₀ = 1), but thereafter ε is zero.

First, we examine the case where the persistence parameter is known with certainty, but the policy effectiveness parameter can only be estimated imprecisely.^[12] Figure 3(a) shows that the uncertainty-aware optimal policy response to the shock in y is more conservative than the naive response. Consequently, using the mean parameter draw to forecast the target variable outcomes in Figure 3(b), the uncertainty-aware policy response means that the target variable takes longer to return to target. Of course, the actual ex-post outcome under both policy responses will depend upon the ‘true’ parameters, which need not coincide with the mean parameter draw.

For the two instrument paths shown in Figure 3(a), we can derive the implied ex-post target variable outcomes at any time horizon for each of the one thousand parameter draws. From this, we derive the distribution of target variable outcomes, which is presented as a histogram in Figure 3(c). In this Figure we only show the distribution of target variable outcomes two periods after the shock. As expected, under naive policy, the distribution of outcomes is approximately normally distributed with mean zero. For the conservative, uncertainty-aware optimal policy, however, the distribution of target variable outcomes for the one thousand parameter draws is slightly skewed and more tightly focused on small positive outcomes. In this example, because the conservative policy response reduces the spread of possible outcomes, it will generate a lower expected sum of squared deviations of y from target and dominates the naive policy response. This, of course, echoes Brainard's result; when there is uncertainty about the effects of policy then it pays to be more conservative with the policy instrument because the larger the change in the instrument, the greater will be the uncertainty about its final effect on the economy.

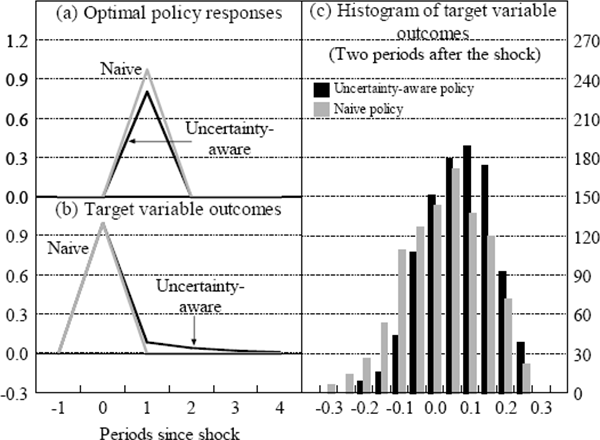
At the other extreme, we now consider the case where the effectiveness of policy is known with certainty, but the degree of persistence can only be imprecisely estimated.^[13] Using the same one thousand parameter draws as before, the results in Figure 4(a) suggest that the uncertainty-aware optimal policy response is now more aggressive than the naive policy response. Figure 4(b) shows the target variable outcomes for these two policy responses using the mean parameter draw.

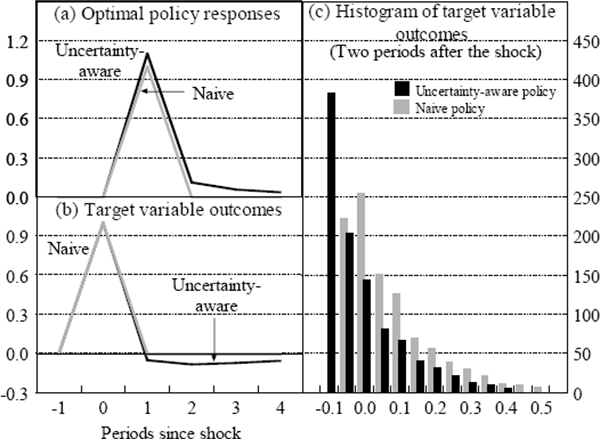
If the policy-maker ignores uncertainty, then the target variable will only follow the path shown in Figure 4(b) if the ‘true’ parameters coincide with the mean parameter draw. The target variable will overshoot, however, if persistence is lower than expected.^[14] In this case, because the economy is less persistent than expected, the overshooting will be rapidly unwound, meaning that the shock is less likely to have a lasting impact on the economy. In contrast, if the target variable undershoots, then persistence must be higher than expected, so the effect of the shock will take longer to dissipate. A policy-maker that is aware of parameter uncertainty will take this asymmetry into account, moving the policy instrument more aggressively in response to a shock.^[15] This will ensure that more persistent outcomes are closer to target at the cost of forcing less persistent outcomes further from target. This reduces the expected losses because the outcomes furthest from target unwind most quickly.

Generally speaking, when there is uncertainty about how persistent the economy is, that is, how a shock to y will feed into future values of y, then it makes sense to be more aggressive with the policy instrument with the hope of minimising deviations of the target variable as soon as possible. In Figure 4(c), for example, the aggressive uncertainty-aware policy response reduces the likelihood of undershooting, at the cost of increasing the chance of overshooting. This policy response dominates, however, because the loss sustained by the many small negative outcomes that it induces is more than offset by the greater loss sustained by the large positive outcomes associated with naive policy.^[16]

These two simple examples show that the implications of parameter uncertainty are ambiguous. Policy should be more conservative when the effectiveness of policy is relatively imprecisely estimated, while policy may be more aggressive when the persistence of the economy is less precisely estimated. In between the two extreme examples which we have considered here, when there is uncertainty about all or most of the coefficients in a model, then one cannot conclude a priori what this entails for the appropriate interest-rate response to a particular shock. In the context of any estimated model, it remains an empirical issue to determine the implications of parameter uncertainty for monetary policy. This is what we do in the next section.

This example also highlights the importance of assuming that monetary authorities never learn about the true model parameters. The monetary authority always observes the outcome in each period of time. If the extent of the policy error in the first period conveys the true value of ρ or θ, then policy could be adjusted to drive y to zero in the next period. Ruling out learning prevents these ex-post policy adjustments, making the initial policy stance time consistent. To the extent that uncertainty is not being resolved through time, this is a relevant description of policy. Additional data may sharpen parameter estimates but these gains are often offset by instability in the underlying parameters themselves. Sack (1997) explored the case in which uncertainty about the effect of monetary policy is gradually resolved through time by learning using a simple model in which the underlying parameters are initially chosen from a stochastic distribution.

Footnotes

Specifically, in this simulation we assume that the persistence parameter ρ takes the value 0.5 with certainty while the policy effectiveness parameter θ is drawn from a normal distribution with mean −0.5 and variance 0.25. [12]

In this case, θ takes the value −0.5 with certainty and ρ is drawn from a normal distribution with mean 0.5 and variance 0.25. [13]

Here an overshooting is defined as a negative target variable outcome because the initial shock was positive. An undershooting, then, is defined as a positive target variable outcome. [14]

Of course, there is a limit on how aggressive policy can be before it causes worse outcomes. [15]

However, in this case, it is important to recognise that if the loss function contained a discount factor then this could reduce the costs of conservative policy. For example, with discounting, the naive policy-maker in Figure 4 will be less concerned about bigger actual losses sustained further into the forecast horizon. This result applies more generally; if policy-makers do not care as much about the future as the present, then they may prefer less activism rather than more. [16]