RDP 1999-10: The Implications of Uncertainty for Monetary Policy 3. An Economic Model

Geoffrey Shuetrim and Christopher Thompson

November 1999

In this paper, rather than constructing a more sophisticated model, we use a simple model which has been developed in previous Reserve Bank research and which was recently applied by de Brouwer and Ellis (1998). Work on constructing a more realistic model for forecasting and policy analysis was beyond the scope of this paper.

The model we use is built around two identities and five estimated relationships determining key macroeconomic variables in the Australian economy: output, prices, unit labour costs, import prices and the real exchange rate. Despite its size, the model captures most aspects of the open economy monetary-policy transmission mechanism, including the direct and indirect influences of the exchange rate on inflation and output. The model is totally linear with only backward-looking expectations on the part of wage and price setters and financial market participants. The equations are estimated separately, using quarterly data from September 1980 to December 1997, except for the real exchange rate equation, which was estimated using quarterly data from March 1985.[4] The specification of the model is summarised in Table 1. The model is described in more detail in Appendix B of de Brouwer and Ellis (1998).

Table 1: Specification of the Model
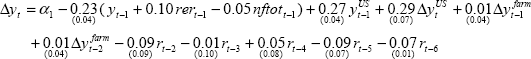
Output(a) Inline Equation
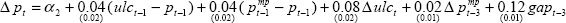
Prices(b) Inline Equation
Unit labour costs(c) 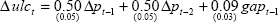Inline Equation
Import prices(d) 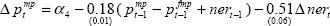Inline Equation
Real exchange rate(e) 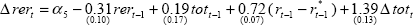Inline Equation
Nominal exchange rate 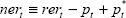Inline Equation
Real interest rate 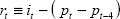Inline Equation
y Real non-farm gross domestic product
rer Real trade-weighted exchange rate
nftot Non-farm terms of trade
yus Real United States gross domestic product
yfarm Real farm gross domestic product
r Real (cash) interest rate
p Treasury underlying consumer price index
ulc Underlying nominal unit labour costs
pmp Tariff-adjusted import prices
gap Output gap (actual output less a production-function based measure of potential output)
pfmp Foreign price of imports (trade-weighted price of exports from Australia's trading partners expressed in foreign currency units)
ner Nominal trade-weighted exchange rate
tot Terms of trade
r* Foreign real short-term interest rate (smoothed GDP-weighted average of real short-term interest rates in the US, Japan and Germany)
p* Foreign price level
i Nominal cash rate (policy instrument)

Notes: All variables except interest rates are expressed in log levels.
Figures in ( ) are standard errors (adjusted for residual heteroscedasticity or autocorrelation where necessary).
(a) The coefficients on the lagged level of rer and nftot were calibrated so that an equal simultaneous rise in both the terms of trade and the real exchange rate results in a net contraction of output in the long run.
(b) As specified, this equation implies linear homogeneity in the long-run relationship between prices, nominal unit labour costs and import prices (this restriction is accepted by the data).
(c) The restriction that the coefficients on lagged inflation sum to unity was imposed (this restriction is accepted by the data) and the equation was estimated by generalised least squares to correct for serial correlation.
(d) As specified, this equation implies linear homogeneity between the domestic price of imports, the nominal exchange rate and the foreign price of imports. This is equivalent to assuming purchasing power parity and full first-stage pass-through of movements in the exchange rate and foreign prices to domestic prices.
(e) A Hausman test failed to reject the null hypothesis that the first difference of the terms of trade was exogenous so results are reported using OLS estimates (OECD industrial production and lagged differences of the terms of trade were used as instruments when conducting the Hausman test).

It is also necessary to specify the preferences of the policy-maker, in this paper, the monetary authority. Specifically, we assume that the policy-maker sets the profile of the policy instrument, the nominal cash rate (short-term interest rate), to minimise the intertemporal loss function:

where gap is the output gap (Table 1), π is the year-ended inflation rate of the underlying CPI; π* is the inflation target specified in year-ended terms and Et is the expectations operator conditional on information available at time t.

The first two terms in this objective function describe the policy-maker's preference for minimising the expected output gap and deviations of expected inflation from target. The third term in the loss function represents the penalty attached to volatility in the policy instrument. This term is included to reduce the monetary authority's freedom to set policy in a way that deviates too far from the observed behaviour of the policy instrument. By penalising volatility in the policy instrument, this term imposes a degree of interest-rate smoothing (Lowe and Ellis 1997).

At each point in time, optimal policy is achieved by minimising the loss function with respect to the path of the policy instrument over the forecast horizon, t + 1 to t + h, subject to the system of equations described in Table 1.

The coefficients, α, β and γ are the relative weights (importance) attached to minimisation of the output gap, deviations of inflation from target and movements in the policy instrument. In this paper, we set α, β and γ equal to 0.02, 0.98 and 0.02 respectively. This particular combination of weights characterises a monetary authority with a strong emphasis on keeping inflation close to target. The weights were selected so that the optimal policy response brings inflation back to target within a reasonable number of years for most common kinds of shocks. There is a much higher weight on inflation than on the output gap because the output gap is an important determinant of inflation. Therefore, policy which concentrates on getting inflation back to target also indirectly aims to close the output gap. While optimal policy is certainly sensitive to the choice of weights, they do not affect the qualitative implications of parameter uncertainty for monetary policy.

This completes the description of the model and the objectives of the policy-maker. The simulations in the following sections report optimal policy responses to shocks that move the model from its steady state, where the steady state is characterised by the error-correction terms in the equations.

The steady-state conditions are satisfied by normalising all of the constants and variables to zero and assuming that the exogenous variables have zero growth rates. This particular steady state has two advantages. First, the zero growth assumption eliminates the need for more sophisticated modelling of the exogenous variables.[5] Second, different parameter estimates imply different long-run relationships, but the zero-level steady state is the only one that satisfies each of these estimated long-run relationships. This means that the results which we present later can be interpreted as deviations from baseline.

Footnotes

Unless otherwise specified, the equations were estimated by ordinary least squares and, where necessary, the variance-covariance matrices of the coefficients were estimated using White's correction for residual heteroscedasticity and the Newey-West correction for residual autocorrelation. [4]

However, in practice, generating forecasts and optimal policy responses from this model would require explicit models for the exogenous variables, which would introduce additional parameter uncertainty. [5]