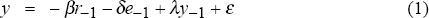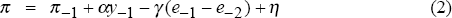RDP 9806: Policy Rules for Open Economies 2. The Model

2.1 Assumptions

The model is an extension of Svensson (1997a) and Ball (1997) to an open economy. The goal is to capture conventional wisdom about the major effects of monetary policy in a simple way. The model is similar in spirit to the more complicated macroeconometric models of many central banks.

The model consists of three equations:

where y is the log of real output, r is the real interest rate, e is the log of the real exchange rate (a higher e means appreciation), π is inflation, and ε, η, and ν are white-noise shocks. All parameters are positive, and all variables are measured as deviations from average levels.

Equation (1) is an open-economy IS curve. Output depends on lags of the real interest rate and the real exchange rate, its own lag, and a demand shock.

Equation (2) is an open-economy Phillips curve. The change in inflation depends on the lag of output, the lagged change in the exchange rate, and a shock. The change in the exchange rate affects inflation because it is passed directly into import prices. This interpretation is formalised in Appendix A, which derives (2) from separate equations for domestic goods and import inflation.

Finally, Equation (3) posits a link between the interest rate and the exchange rate. It captures the idea that a rise in the interest rate makes domestic assets more attractive, leading to an appreciation. The shock ν captures other influences on the exchange rate, such as expectations, investor confidence, and foreign interest rates. Equation (3) is similar to reduced-form equations for the exchange rate in many textbooks.

The central bank chooses the real interest rate r. One can interpret any policy rule as a rule for setting r. Using Equation (3), one can also rewrite any rule as a rule for setting e, or for setting some combination of e and r.

A key feature of the model is that policy affects inflation through two channels. A monetary contraction reduces output and thus inflation through the Phillips curve, and it also causes an appreciation that reduces inflation directly. The lags in Equations (1) – (3) imply that the first channel takes two periods to work: a tightening raises r and e contemporaneously, but it takes a period for these variables to affect output and another period for output to affect inflation. In contrast, the direct effect of an exchange-rate change on inflation takes only one period. These assumptions capture the common view that the direct exchange-rate effect is the quickest channel from policy to inflation.

2.2 Calibration

In analysing the model, I will interpret a period as a year. With this interpretation, the time lags in the model are roughly realistic. Empirical evidence suggests that policy affects inflation through the direct exchange-rate channel in about a year, and through the output channel in about two years (e.g. Reserve Bank of New Zealand 1996; Lafleche 1996).

The analysis will use a set of base parameter values. Several of these values are borrowed from the closed-economy model in Ball (1997). Based on evidence discussed there, I assume that λ, the output-persistence coefficient, is 0.8; that α, the slope of the Phillips curve, is 0.4; and that the total output loss from a one-point rise in the interest rate is 1.0. In the current model, this total effect is β + δθ : β is the direct effect of the interest rate and δθ is the effect through the exchange rate. I therefore assume β + δθ = 1.0.

The other parameters depend on the economy's degree of openness. My base values are meant to apply to medium-to-small open economies such as Canada, Australia, and New Zealand. My main sources for the parameters are studies by these countries' central banks. I assume γ = 0.2 (a one per cent appreciation reduces inflation by two tenths of a point) and θ = 2.0 (a one-point rise in the interest rate causes a two per cent appreciation). I also assume β / δ = 3.0, capturing a common rule of thumb about IS coefficients. Along with my other assumptions, this implies β = 0.6 and δ = 0.2.^[2]

Footnote

Examples of my sources for base parameter values are the Canadian studies of Longworth and Poloz (1986) and Duguay (1994) and the Australian study of Gruen and Shuetrim (1994). [2]