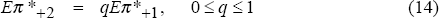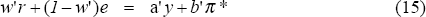RDP 9806: Policy Rules for Open Economies 6. Long-run Inflation Targets

This section presents the good news about inflation targets. The problems described in the previous section can be overcome by modifying the target variable. In light of earlier results, a natural modification is to target long-run inflation, π^*.

6.1 The Policies

Strict long-run inflation targeting is defined as the policy that minimises the variance of π^* = π + γe₋₁. To see its implications, note that Equation (2) can be rewritten as:

This equation is the same as a closed-economy Phillips curve, except that π^* replaces π. The exchange rate is eliminated, so policy affects π^* only through the output channel. Thus policy affects π^* with a two-period lag, and strict targeting implies:

In contrast to a two-period-ahead target for total inflation, Equation (13) defines a unique policy.

There are two related motivations for targeting π^* rather than π. First, since π^* is not influenced by the exchange rate, policy uses only the output channel to control inflation. This avoids the exchange-rate ‘whiplashing’ discussed in the previous section. Second, as discussed in Section 3, π^* gives the level of inflation with transitory exchange-rate effects removed. π^* targeting keeps underlying inflation on track.

In addition to strict π^* targeting, I consider gradual adjustment of π^*:

This rule is the similar to the gradual-adjustment rule that is optimal in a closed economy. Policy adjusts Eπ^*₊₂ part of the way to the target from Eπ^*₊₁, which it takes as given. The motivation for adjusting slowly is to smooth the path of output.

In practice, countries with inflation targets do not formally adjust for exchange rates in the way suggested here. However, adjustments may occur implicitly. For example, a central-bank economist once told me that inflation was below his country's target, but that this was desirable because the currency was temporarily strong, and policy needed to ‘leave room’ for the effects of depreciation. Keeping inflation below its official target when the exchange rate is strong is similar to targeting π^*.

6.2 Results

To examine π^* targets formally, I substitute Equations (12) and (1) into condition Equation (14). This leads to the instrument rule implied by π^* targets:

where w′= (β / (β +δ), a′ = (1 − q + λ) / (β +δ), b′ = (1−q) / [α(β +δ)]

This equation includes the same variables as the optimal rule in Section 3, but the coefficients are different. The MCI weights are given exactly by the relative sizes of β and δ; for base parameters, w'=0.75. The coefficients on y and π^* depend on the adjustment speed q.

Appendix B calculates the variances of output and inflation under π^* targeting. Figure 3 plots the results for q between zero and one. The case of strict π^* targeting corresponds to the Northwest corner of the curve. For comparison, Figure 3 also plots the set of efficient policies from Figure 1.

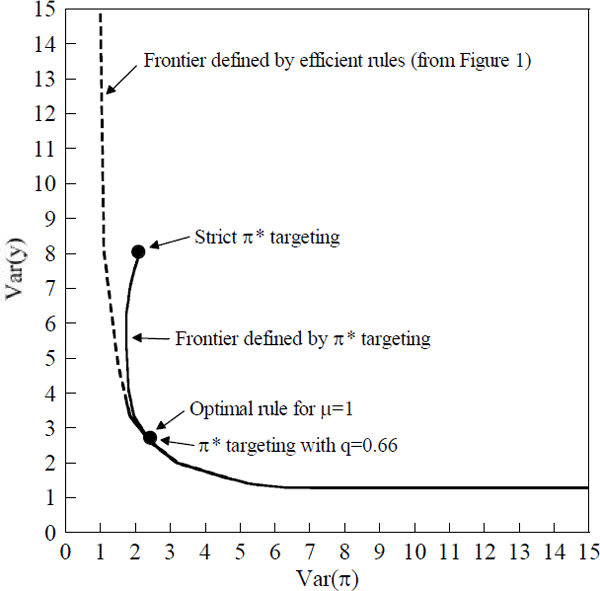
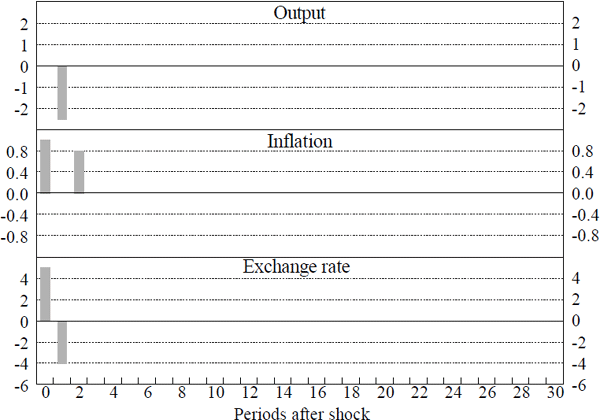
The Figure shows that targeting π^* produces more stable output than targeting π. This is true even for strict π^* targets, which produce an output variance of 8.3, compared to 25.8 for π targets. Figure 4 shows the dynamic effects of an inflation shock under π^* targets, and confirms that this policy avoids oscillations in output. Strict π^* targeting is, however, moderately inefficient. There is an efficient instrument rule that produces an output variance of 8.3 and an inflation variance of 1.2. Strict π^* targets produce the same output variance with an inflation variance of 1.9.

As the parameter q is raised, so adjustment becomes slower, we move Southeast on the frontier defined by π^* targeting. This frontier quickly moves close to the efficient frontier. Thus, as long as policy-makers put a non-negligible weight on output variance, there is a version of π^* targeting that closely approximates the optimal policy. For example, for equal weights on inflation and output variances, the optimal policy has an MCI weight w of 0.70, and output and π^* coefficients of 1.35 and 1.06. For a π^* target with q = 0.66, the corresponding numbers are 0.75, 1.43, and 1.08. The variances of output and inflation are 2.50 and 2.44 under the optimal policy and 2.48 and 2.48 under π^* targeting.