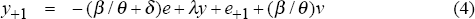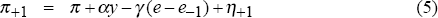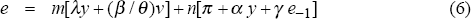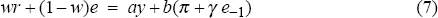RDP 9806: Policy Rules for Open Economies 3. Efficient Instrument Rules
July 1998
- Download the Paper 139KB
Following Taylor (1994), the optimal policy rule is defined as the one that minimises a weighted sum of output variance and inflation variance. The weights are determined by policy-makers tastes. As in Ball (1997), an ‘efficient’ rule is one that is optimal for some weights, or equivalently a rule that puts the economy on the output variance/inflation variance frontier. This section derives the set of efficient rules in the model.
3.1 The Variables in the Rule
As discussed earlier, we can interpret any policy rule as a rule for r, a rule for e, or a rule for a combination of the two. Initially, it is convenient to consider rules for e. To derive the efficient rules, I first substitute Equations (3) into (1) to eliminate r from the model. I shift the time subscripts forward to show the effects of the current exchange rate on future output and inflation. This yields:
Consider a policy-maker choosing the current e. One can define the state variables of the model by two expressions corresponding to terms on the right sides of Equations (4) and (5): λy + (β /θ)ν, and π + αy + γe−1. The future paths of output and inflation are determined by these two expressions, the rule for choosing e, and future shocks. Since the model is linear quadratic, one can show the optimal rule is linear in the two state variables:
where m and n are constants to be determined.
In Equation (6), the choice of e depends on the exchange-rate shock ν as well as observable variables. By Equation (3), ν can be replaced by e – θr. Making this substitution and rearranging terms yields:
where w = mβθ / (θ−mβ+mβθ), a = θ(mλ + nα)/(θ-mβ + mβθ), b = nθ/(θ − mβ + mβθ)
This expresses the optimal policy as a rule for an average of r and e.
3.2 Interpretation
In the closed-economy model of Svensson and Ball, the optimal policy is a Taylor rule: the interest rate depends on output and inflation. Equation (7) modifies the Taylor rule in two ways. First, the policy variable is a combination of r and e. And second, inflation is replaced by π + γe−1, a combination of inflation and the lagged exchange rate. Each of these modifications has a simple interpretation.
The first result supports the practice of using an average of r and e – a ‘Monetary Conditions Index’ – as the policy instrument. Several countries follow this approach, including Canada, New Zealand and Sweden (see Gerlach and Smets 1996). The rationale for using an MCI is that it measures the overall stance of policy, including the stimulus through both r and e. Policy-makers shift the MCI when they want to ease or tighten. When there are shifts in the e/r relation – shocks to Equation (3) – r is adjusted to keep the MCI at the desired level.
The second modification of the Taylor rule is more novel. The term π + γe−1 can be interpreted as a long-run forecast of inflation under the assumption that output is kept at its natural level. With a closed-economy Phillips curve, this forecast would simply be current inflation. In an open economy, however, inflation will change because the exchange rate will eventually return to its long-run level, which is normalised to zero. For example, if e was positive in the previous period, there will be a depreciation of e−1 at some point starting in the current period. By Equation (2), this will raise inflation by γe−1 at some point after the current period. I will use the term ‘long-run inflation’ and the symbol π* to stand for π + γe−1.
More broadly, one can interpret π + γe−1 as a measure of inflation that filters out direct but temporary effects of the exchange rate. For a given output path, an appreciation causes inflation to fall, but it will rise again by γe−1 when the appreciation is reversed. The adjustment from π to π* is similar in spirit to calculations of ‘core’ or ‘underlying’ inflation by central banks. These variables are measures of inflation adjusted for transitory influences such as changes in indirect taxes or commodity prices. Many economists argue that policy should respond to underlying inflation and ignore transitory fluctuations. My model supports this idea for the case of fluctuations caused by exchange rates.
3.3 Efficient Coefficients for the Rule
The coefficients in the policy rule (7) depend on the constants m and n, which are not yet determined. The next step is to derive the efficient combinations of m and n – the combinations that put the economy on the output variance/inflation variance frontier. As discussed in Appendix B, the set of efficient policies depends on the coefficients in Equations (1) – (3) but not on the variances of the three shocks (although these variances determine the absolute position of the frontier). For base parameter values, I compute the variances of output and inflation for a given m and n and then search for combinations that define the frontier.
Figure 1 presents the results in a graph. The Figure shows the output variance/inflation variance frontier when the variance of each shock is one. For selected points on the frontier, the graph shows the policy-rule coefficients that put the economy at that point. It also shows the weights on output variance and inflation variance that make each policy optimal.
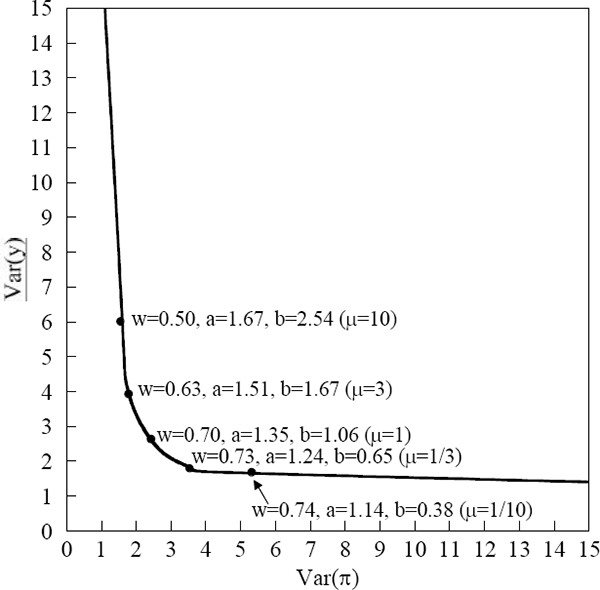
Note: Objective function = Var(y) + μVar(π)
Two results are noteworthy. The first concerns the weights on r and e in the Monetary Conditions Index. There is currently a debate among economists about the appropriate weights. Some argue that the weights should be proportional to the coefficients on e and r in the IS equation (for example, Freedman 1994). For my base parameters, this implies w=0.75, i.e. weights of 0.75 on r and 0.25 on e. Others suggest a larger weight on e to reflect the direct effect of the exchange rate on inflation (see Gerlach and Smets 1996). In my model, the optimal weight on e is larger than 0.25, but by a small amount. For example, if the policy-makers objective function has equal weights on output and inflation variances, the MCI weight on e is 0.30. The weight on e is much smaller than its relative short-run effect on inflation. The only exceptions occur when policy-makers objectives have very little weight on output variance.[3]
The second result concerns the coefficients on y and π*, and how they compare to the optimal coefficients on y and π in a closed economy. Note that a one-point rise in the interest rate, which also raises the exchange rate, raises the MCI by a total of w + θ(1 − w). Dividing the coefficients on y and π* by this expression yields the responses of r to y and π* – the analogues of Taylor-rule coefficients in a closed economy. For equal weights in policy-makers objective functions, the interest-rate response to output is 1.04 and the response to π* is 0.82. Assuming the same objective function, the corresponding responses in a closed economy are 1.13 for output and 0.82 for inflation (Ball 1997). Thus the sizes of interest-rate movements are similar in the two cases.
Footnote
One measure of the overall effect of e on inflation is the effect through appreciation in one period plus the effect through the Phillips curve in two periods. This sum is γ + δα = 0.28. The corresponding effect of r on inflation is βα = 0.24. The MCI would put more weight on e than on r if it were based on these inflation effects. [3]