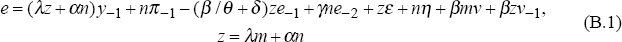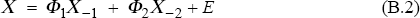RDP 9806: Policy Rules for Open Economies Appendix B: The Variances of Output and Inflation

Here, I describe the computation of the variances of output and inflation under alternative policies. Consider first the rule given by Equations (6) and (7). Substituting Equations (4) and (5) into (6) yields an expression for the exchange rate in terms of lagged e, π, and y:

This equation and Equations (4) and (5) define a vector process for e, π, and y:

where X = [y π e]'

The elements of E depend on the current and once-lagged values of white-noise shocks. Thus E follows a vector MA(1) process with parameters determined by the underlying parameters of the model. X follows an ARMA(2,1) process. For given parameter values and given values of the constants m and n, one can numerically derive the variance of X using standard formulas (see Hendry 1995, Section 11.3). To determine the set of efficient policies, I search over m and n to find combinations that minimise a weighted sum of the output and inflation variances.

To determine the variances of output and inflation under a π^* target, Equation (15), note that Equation (15) is equivalent to Equation (7) with m set to θ / (θδ + β) and n set to θ(1 − q) / [α(θδ + β)]. For a given q, the variances of output and inflation under Equation (15) are given by the variances for the equivalent version of Equation (7).