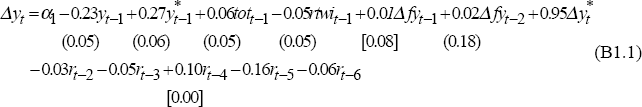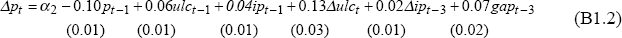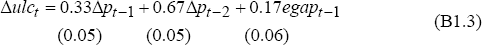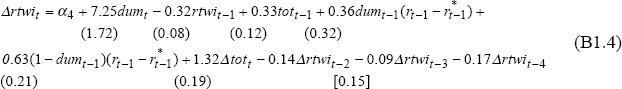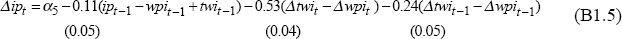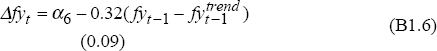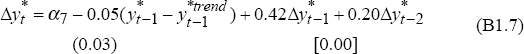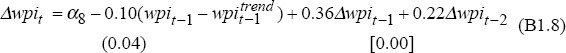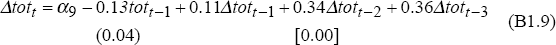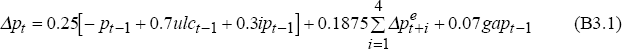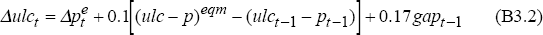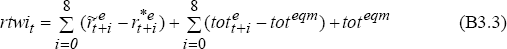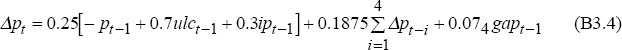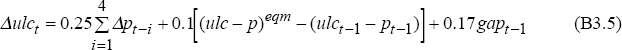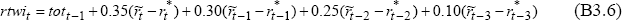RDP 9803: Forward-Looking Behaviour and Credibility: Some Evidence and Implications for Policy Appendix B: A Framework for Analysis
February 1998
- Download the Paper 344KB
B.1 The Model in de Brouwer and O'Regan (1997)
Most equations are written in error-correction form to capture long-run tendencies and relationships between variables, as well as dynamics. Parameters are generally estimated. The specifications of the equations, diagnostics and comments are given below. Numbers in parentheses ( ) are standard errors. Numbers in brackets [ ] are p-values. When lags of a variable enter an equation, the p-value for a joint test of their significance is given. All variables except interest rates are in log levels multiplied by 100. Equations are estimated using quarterly data from 1980:Q3 to 1996:Q3. The analytical framework draws on a number of published Bank papers and the contribution of several Reserve Bank economists, especially David Gruen, Geoff Shuetrim and John Romalis.
Endogenous Variables
Output
ARCH(4) test: 1.62[0.81] LM(4) serial correlation : 4.61[0.42]  Jarque-Bera test: 1.44[0.49] Breusch-Pagan test: 17.7[0.06] Standard error: 0.60
Jarque-Bera test: 1.44[0.49] Breusch-Pagan test: 17.7[0.06] Standard error: 0.60
where y is non-farm output, y* is OECD output, tot is the terms of trade, rtwi is the real TWI, r is the real cash rate and fy is farm output. The coefficients on the lagged levels of the terms of trade and real exchange rate are calibrated so that a 10 per cent rise in the terms of trade boosts output by 2.4 per cent and a 10 per cent appreciation of the real exchange rate reduces output by 2 per cent in the long run. The equation is based on Gruen and Shuetrim (1994) and Gruen, Romalis and Chandra (1997).
Prices
ARCH(4) test: 2.79[0.59] LM(4) serial correlation : 3.51[0.48] 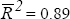 Jarque-Bera test: 2.59[0.27] Breusch-Pagan test: 10.3 [0.07] Standard error: 0.24
Jarque-Bera test: 2.59[0.27] Breusch-Pagan test: 10.3 [0.07] Standard error: 0.24
where p is Treasury underlying CPI, ulc is a measure of underlying unit labour costs, ip is tariff-adjusted import prices and gap is actual less linear-trend output. The restriction that the coefficients on prices, unit labour costs and import prices sum to zero is imposed. The equation is based on de Brouwer and Ericsson (1995).
Unit Labour Costs
ARCH(4) test: 5.48[0.24] LM(4) serial correlation : 4.13[0.39] 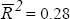 Jarque-Bera test: 0.08[0.96] Breusch-Pagan test: 4.43[0.22] Standard error: 0.46
Jarque-Bera test: 0.08[0.96] Breusch-Pagan test: 4.43[0.22] Standard error: 0.46
where egap is the output gap plus 1 per cent (which is an estimate of the output gap required to generate the disinflation that occurred over the sample period). The equation was estimated by generalised least squares to correct serial correlation, and with the restriction that the coefficients on lagged inflation sum to unity.
Real Exchange Rate
ARCH(4) test: 4.51[0.34] LM(4) serial correlation : 5.97[0.20] 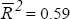 Jarque-Bera test: 1.48[0.49] Breusch-Pagan test: 5.46[0.79] Standard error: 2.74
Jarque-Bera test: 1.48[0.49] Breusch-Pagan test: 5.46[0.79] Standard error: 2.74
where dum is a dummy variable which takes a value of one for 1980:Q3 to 1984:Q4 inclusive and zero otherwise; and r* is the world real short interest rate. The equation is based on Gruen and Wilkinson (1991), Blundell-Wignall, Fahrer and Heath (1993) and Tarditi (1996).
Import Prices
ARCH(4) test: 0.51[0.97] LM(4) serial correlation : 4.59[0.33] 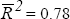 Jarque-Bera test: 3.42[0.18] Breusch-Pagan test: 4.96[0.17] Standard error: 1.42
Jarque-Bera test: 3.42[0.18] Breusch-Pagan test: 4.96[0.17] Standard error: 1.42
where wpi is Australia's trading partner weighted average export prices and twi is the nominal TWI.
Exogenous Variables
Farm output, foreign output and foreign export price are estimated as ‘trend correction’ models by which growth in the variable is regressed against a constant and the deviation of the level from a linear trend. This implies that the exogenous variables are not random walks, but return to trend after a shock.
Farm Output
ARCH(4) test: 3.60[0.46] LM(4) serial correlation : 10.7[0.03] 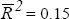 Jarque-Bera test: 179[0.00] Breusch-Pagan test: 17.65[0.00] Standard error: 8.32
Jarque-Bera test: 179[0.00] Breusch-Pagan test: 17.65[0.00] Standard error: 8.32
where fytrend is the trend level of farm output.
Foreign Output
ARCH(4) test: 8.32[0.08] LM(4) serial correlation : 2.50[0.64] 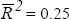 Jarque-Bera test: 1.51[0.47] Breusch-Pagan test: 0.50[0.92] Standard error: 0.36
Jarque-Bera test: 1.51[0.47] Breusch-Pagan test: 0.50[0.92] Standard error: 0.36
where y*trend is the trend level of OECD output, estimated from 1980:Q4 to 1996:Q3.
Foreign Export Price
ARCH(4) test: 3.29[0.51] LM(4) serial correlation : 7.12[0.13] 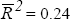 Jarque-Bera test: 1.74[0.42] Breusch-Pagan test: 0.12[0.99] Standard error: 1.05
Jarque-Bera test: 1.74[0.42] Breusch-Pagan test: 0.12[0.99] Standard error: 1.05
where wpitrend is the trend of the Australian trading partner weighted average of world export prices. The trend was estimated over 1980:Q3 to 1996:Q3, while Equation (A8) was estimated over 1981: Q2 to 1996:Q3.
Terms of Trade
ARCH(4) test: 0.01[0.99] LM(4) serial correlation : 1.86[0.76] 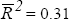 Jarque-Bera test: 4.20[0.12] Breusch-Pagan test: 3.30[0.35] Standard error: 1.74
Jarque-Bera test: 4.20[0.12] Breusch-Pagan test: 3.30[0.35] Standard error: 1.74
Foreign Real Interest Rate
ARCH(4) test: 9.11[0.06] LM(4) serial correlation : 6.89[0.14] 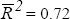 Jarque-Bera test: 1.86[0.40] Breusch-Pagan test: 3.840[0.05] Standard error: 0.64
Jarque-Bera test: 1.86[0.40] Breusch-Pagan test: 3.840[0.05] Standard error: 0.64
Identities
Nominal Exchange Rate
where p* is the foreign price level, a trade-weighted average of foreign consumer price indices.
See de Brouwer and O'Regan (1997) for a full description of the data sources.
B.2 Simulation Analysis
To assess the properties of the various rules, simulations were run for each rule and set of weights using the framework of equations described in Appendix B.1 above. Starting in equilibrium, the system was run over 200 periods using normal random errors for each equation which embody the historical covariance of those errors. The methodology follows Bryant, Hooper and Mann (1993, pp. 240–241).
For all the equations excluding the import price equation, a variance-covariance matrix of the residuals is generated from the variances of the equations and the correlation matrix of the historical residuals. The upper triangle of Table B2.1 shows the correlation coefficients, the main diagonal the variances of each of the series, and the lower triangle the covariances of the variables. The lower triangle of Table B2.1 is copied and transposed into the upper triangle to obtain the symmetric variance-covariance matrix, ∑. The variance-covariance matrix is transformed by a Choleski decomposition to yield a triangular matrix, P, which multiplied with its transpose gives the original matrix: ∑ = PP′. In each period a vector of random errors, et, is drawn from a distribution of a standard normal random variable with a mean of 0 and a variance of 1. To calibrate the shocks with the historical covariances, et is multiplied by the lower triangular P, giving a vector ut = Pet. The elements of ut are the shocks used in the simulations. The same shocks were used in all the simulations. The simulations are performed using GAUSS (for the current-dated information rules) and Mathematica 3.0 (for the optimal policy and forward-looking Taylor-type rule cases), and the seed for the random number generator for 200 shocks is 1.
For the purposes of the simulations, the constant terms in the equations in Appendix B.1 are calibrated to place the system in equilibrium at the initial period. To place the system in equilibrium in the starting period, the initial value for output, prices, unit labour costs, the exchange rate, farm output, import prices, the terms of trade is 100. The calibrated constant term for output is −3.80, for inflation is 0.53, for the real exchange rate is −1.55, for import prices is 11.21, for world output is 0.26, for the terms of trade is 13.46, for world prices is 0.26, and for farm output is 0.56.
| Farm output | Foreign output | Non-farm output | Unit labour costs | Price | Terms of trade | Real exchange rate | World export prices | World real interest rate | |
|---|---|---|---|---|---|---|---|---|---|
| Farm output | 69.2451 | 0.1494 | 0.0810 | 0.0649 | −0.1442 | −0.1713 | 0.1993 | 0.0209 | −0.0824 |
| Foreign output | 0.4520 | 0.1322 | −0.1078 | −0.0329 | 0.1814 | 0.1677 | −0.0225 | −0.1627 | −0.1803 |
| Non-farm output | 0.4028 | −0.0234 | 0.3567 | 0.1134 | −0.0035 | −0.1389 | 0.0500 | 0.0324 | −0.1206 |
| Unit labour costs | 0.2499 | −0.0055 | 0.0313 | 0.2141 | −0.1177 | 0.1579 | 0.0084 | 0.1636 | −0.1487 |
| Price | −0.2894 | 0.0159 | −0.0005 | −0.0131 | 0.0582 | −0.0791 | −0.1147 | −0.2011 | −0.0611 |
| Terms of trade | −2.4811 | 0.1062 | −0.1444 | 0.1272 | −0.0332 | 3.0292 | 0.1348 | 0.3592 | 0.1806 |
| Real exchange rate | 4.5409 | −0.0224 | 0.0817 | 0.0106 | −0.0758 | 0.6425 | 7.4982 | 0.1636 | −0.0311 |
| World export prices | 0.1831 | −0.0623 | 0.0204 | 0.0798 | −0.0511 | 0.6588 | 0.4720 | 1.1104 | 0.0494 |
| World real interest rate | −0.4368 | −0.0418 | −0.0459 | −0.0439 | −0.0094 | 0.2004 | −0.0543 | 0.0332 | 0.4063 |
B.3 The Stylised Model-consistent and Extrapolative Models
The price equations (consumer prices, unit labour costs and the exchange rate) in the model outlined earlier in Appendix B.1 are adjusted to take explicit account of different expectations processes. When expectations are fully model-consistent, these equations are as follows. Inflation is:
where p is the price level, ulc is unit labour costs, ip is import prices in domestic currency, gap is actual output less potential (estimated as a linear trend) and a superscript e indicates a model-consistent expected value at time t.
Growth in unit labour costs is:
where the superscript eqm indicates an equilibrium value.
The real exchange rate is:
where an asterisk denotes a foreign variable, tot is the terms of trade, rtwi
is the real exchange rate in terms of domestic currency (so a rise is an appreciation), 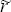 is the
real interest rate less the risk premium, and r is the real interest rate.
is the
real interest rate less the risk premium, and r is the real interest rate.
When expectations are fully extrapolative, inflation is:
Unit labour costs growth is:
And the real exchange rate is:
Domestic non-farm output, farm output, foreign output, foreign prices, foreign interest rates and the terms of trade are generated using the equations set out in Appendix B.1.