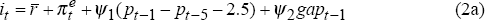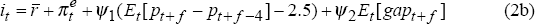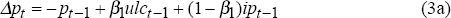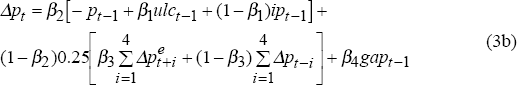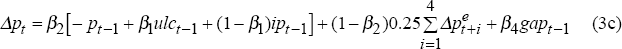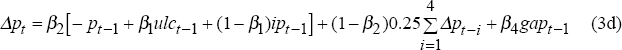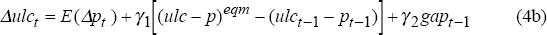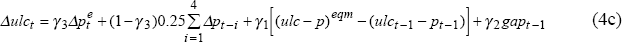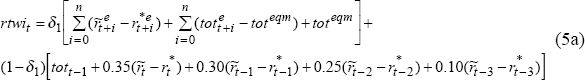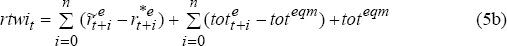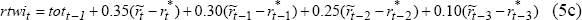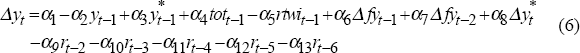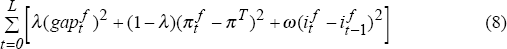RDP 9803: Forward-Looking Behaviour and Credibility: Some Evidence and Implications for Policy 3. Policy Implications
February 1998
- Download the Paper 344KB
Expectations play a key role in most economic models, and models of the macroeconomy are no exception. For example, one of the main determinants of economic growth in the short to medium term is the real interest rate, which is defined as the nominal interest rate less the expected rate of inflation. Similarly, models of price and wage adjustment typically include the expected inflation rate, and models of the exchange rate can include not just current values of the driving variables but also their expected future values. In many cases, specifying how these expectations are formed has profound implications for the outcomes and predictions of the model.
Perhaps the simplest approach to modelling expectations is to assume that the expected value of a variable is a weighted combination of its current and recent values. In the case of the real interest rate, for example, expected inflation would be equal to current annual inflation, so that the real interest rate is the nominal interest rate less the current rate of inflation. This characterisation is often referred to as ‘backward looking’ expectations, which is somewhat paradoxical since the fact that expectations are being formed at all indicates that people are thinking about the future. However, the basic idea in this formulation is that people form their expectations of the future by looking at recent history, or, in other words, looking backwards. The terms ‘extrapolative’ or ‘adaptive’ expectations convey a similar meaning, and in this paper, we use ‘backward looking’, ‘extrapolative’ and ‘adaptive’ interchangeably.
An alternative approach is to assume that people form their expectations of the future with reference to the structure of the economy, including how the central bank responds to various pieces of information. Expectations formed in this way are usually called ‘model consistent’ or ‘forward looking’ expectations, although the latter term is clearly tautological. When expectations are model-consistent, an announced change in the way the central bank operates, for example, can change people's expectations of the future and thus the way the economy evolves. Of course, the policy response has to be seen to be credible for this to happen; if it is not credible, the public will not change the way they view the future. Thus in any modelling exercise in which it is assumed that people know the structure of the economy, it is also necessary to make an assumption about the credibility of policy responses. In this paper, when we use model-consistent expectations we assume that the public knows the way the central bank operates and that the central bank does not deviate from this expected behaviour.
In this section, we consider models of the economy that are based on both backward-looking and model-consistent expectations, and we include a hybrid version in which expectations are a mix of these two approaches. In Section 3.1, we use a model in which people have backward-looking expectations to examine how forward-looking behaviour on the part of the central bank can affect the variability of inflation and the output gap. In Section 3.2, we focus on the way expectations of people other than policy-makers can affect the way shocks influence economic outcomes. Model-consistent expectations reduce the variability in inflation and output, although when sectors in the economy have different inflation expectations, the ex ante real interest rates that affect output and the exchange rate differ, which we show can generate either oscillations or overshooting in the exchange rate. In Section 3.3, we assess different expectations processes in this model from the perspective of optimal monetary policy, to see whether policy-makers can compensate for the greater variability in inflation and output that occurs when people form their expectations of the future by extrapolating from the past.
3.1 The Benefits of Forward-looking Policy
One characterisation of monetary policy is that policy-makers follow a feedback rule, by which they raise the short-term real interest rate above its ‘neutral’ rate when current inflation is above target or when current output is above potential, and vice versa, which we call a Taylor-type rule for short (Taylor 1993; Bryant, Hooper and Mann 1993). For example, if policy-makers react to current data in setting interest rates, one possible rule is:
where 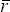 is
the neutral real cash rate, πe is expected annual inflation,[5] p is the
price level, 2.5 is the annual inflation target, gap is the output gap (actual less
potential output) and the information variables are dated at t−1 since, in
general, only statistics for the previous quarter are available in the current quarter. But if
policy-makers set the instrument with respect to model-based forecasts of inflation and the
output gap,[6]
the rule becomes:
is
the neutral real cash rate, πe is expected annual inflation,[5] p is the
price level, 2.5 is the annual inflation target, gap is the output gap (actual less
potential output) and the information variables are dated at t−1 since, in
general, only statistics for the previous quarter are available in the current quarter. But if
policy-makers set the instrument with respect to model-based forecasts of inflation and the
output gap,[6]
the rule becomes:
where Et indicates an expectation at time t and f is the forecast horizon. Such Taylor-type rules are not an exact representation of policy, since the economy, shocks and central bank reaction functions are considerably more complex than suggested by simple rules, although the focus on deviations of inflation from target and output from potential is generally considered to be a good first approximation.
Using stochastic simulation of a simple data-consistent model of the Australian economy with adaptive expectations processes (reproduced in Appendix B), de Brouwer and O'Regan (1997) showed that policy-makers following a Taylor-type rule can more successfully reduce the variability of inflation around target, and of output around potential, when they set interest rates based on forecasts of inflation and output, instead of relying on the most recent available data on these variables. Interest rates affect economic activity and inflation with a lag, and so policy-makers can reduce variability if they change rates now in anticipation of future developments in activity and inflation. This is the well known rationale for pre-emptive monetary policy.
Assuming that policy-makers forecast on the basis of unchanged future policy, defined as a constant nominal interest rate, de Brouwer and O'Regan (1997) reported that simple forward-looking policy rules based on two-period ahead forecasts do better than simple rules based on other forecast horizons. While the unchanged-policy assumption is fairly standard in policy analysis, it is undesirable in model-based exercises since fixing the nominal or real interest rate over the forecast horizon implies that policy accommodates inflation shocks, in turn increasing the variability of inflation and output. Moreover, the supposition that sometimes policy-makers set interest rates based on a particular reaction function but then at other times keep rates constant, is inconsistent with both the model and the argument that the reaction weights in such a rule are efficient.
The constant-rate assumption also implies greater variability in interest rates (and inflation and output) since it rules out policy-makers planning a path for interest rates. When interest rates are assumed to be constant over the forecast horizon, policy-makers are unable to allow for the effect of their own future reaction on the forecast variables, and hence they overestimate the variability of inflation and output. In modeling exercises such as this, policy-makers therefore over-react to shocks in the current period, only to partially reverse the response in subsequent periods (see Appendix C for more details). Accordingly, in this paper we examine which forecast horizon most reduces variability in inflation and output assuming that policy-makers make their forecasts conditional on the application of the given policy rule over the forecast horizon.
We also search for reaction weights across all possible values in a rule, and do not restrict these coefficients to take a value of two or less, as was the case in earlier work. This is important because we use model-consistent policy rules in the forecast period. Since policy is assumed to be responding in each of the forecast periods, the expected deviation of inflation from target following an inflation shock, for example, is likely to be smaller the further out is the forecast period. To achieve a given change in the interest rate, the reaction weight has to be larger since the end-point deviation is smaller.
We turn now to the results of the stochastic simulation.[7] Figure 4 shows the trade-off between the variability of inflation and the output gap when three alternative sets of data – the latest data release, four-quarter ahead forecasts and six-quarter ahead forecasts of inflation and the output gap – are used in the Taylor-type rule. Each curve shows the efficient set of outcomes for different reaction weights for each rule, where a set of reaction weights is said to be ‘efficient’ if it minimises the variability in inflation or the output gap, given the variability in the other. The curves are convex, with each further reduction in the variability of inflation or output coming at the cost of an ever-larger increase in the variability of the other.
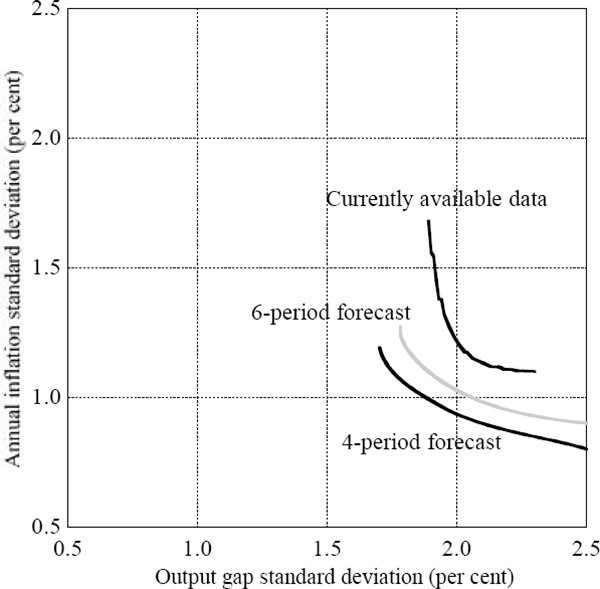
While there is an irreducible variability in inflation and output, these variabilities fall substantially when policy-makers set interest rates with reference to their conditional forecasts, rather than the most recently available statistics. For example, the ‘best’ that policy-makers who react to actual inflation and the output gap can do is to reduce the standard deviation of inflation to about 1.1 per cent. But if they use their four-period ahead forecasts, the ‘best’ standard deviation is about 0.8 per cent. For this model and draw of shocks, the best horizon in terms of minimising the variability in inflation and the output gap using a simple rule is four quarters. Given that data for the current quarter are not yet observable, this implies that the rule explicitly uses forecasts for five periods.
This forecast horizon is well within the control lag of policy in this model, which Haldane (1997) has shown to be necessary if policy is to be stabilising. In this model, for example, there is a two-period lag from policy to inflation via the exchange rate. The control lag from policy to inflation via the output gap is at least three periods, since policy affects output with a lag of at least two periods (both directly and indirectly through the real exchange rate) and the output gap in turn affects wages, and hence, inflation, with a one period lag.
But Figure 4 also shows that policy-makers cannot rely on ever-longer forecast horizons in a simple rule. The forecast-error variance rises as the forecast horizon is extended further out. Even if everyone knows the ‘true’ model of the economy and forms forecasts based on this, the world is stochastic, and the realisations differ from the expected values. At some stage, the increase in forecast-error variance dominates the stabilising properties of pre-emptive policy.
In this model, the reduction in the variability of inflation and output is smaller when policy-makers use forecasts six quarters out, compared to when they use forecasts four quarters out. The four-quarter forecast horizon, however, is not as short as it might seem, since the four-quarter forecast of the output gap helps predict inflation a further one to two quarters out through the wages process and a further three quarters out directly through its effect on the mark-up. This essentially means that interest rates are responding to forecasts of inflation four to seven quarters out. It is worth noting that the rules we are considering here restrict policy-makers to set interest rates with respect to the forecasts of only one particular period in the future. A more efficient, but complex, rule would be for policy-makers to set the interest rate based on the full profile of inflation and output over time, with different weights on each period's forecasts.
Simple forward-looking policy rules can substantially reduce the variability in inflation and output. But as policy becomes more forward looking, it also becomes more activist, in the sense that interest rates are moved around considerably more than otherwise. Table 2 sets out some reaction weights and associated standard deviations on interest rate changes on some of the efficient frontiers shown above. As policy becomes more forward looking, the variability in interest rates increases.
| Taylor-type rule | Inflation reaction coefficient | Output gap reaction coefficient | Inflation standard deviation | Output gap standard deviation | Δ interest rate standard deviation |
|---|---|---|---|---|---|
| Current data | 0.1 | 1.0 | 1.55 | 1.91 | 0.98 |
| 0.5 | 1.3 | 1.27 | 1.97 | 1.35 | |
| 1.4 | 1.4 | 1.10 | 2.30 | 1.82 | |
| 4-period forecast | 2.0 | 3.5 | 1.19 | 1.70 | 2.46 |
| 5.0 | 4.0 | 1.03 | 1.82 | 3.36 | |
| 8.0 | 4.0 | 0.95 | 1.97 | 4.02 |
Although this volatility seems implausibly high when compared to historical experience, some other combinations of reaction weights can generate much lower instrument volatility with only a small cost in increased variability in inflation and the output gap. For example, the inflation and output reaction weights (8, 4) shown in Table 2 generate a standard deviation of the quarterly change in nominal rates which is greater than 4 per cent to achieve standard deviations of inflation and the output gap of 0.95 per cent and 1.97 per cent respectively. The near-efficient weights of (2.8, 1), however, reduce the quarterly standard deviation of interest rate changes to 1.38 per cent, but only at the cost of an increase in the standard deviation of inflation of less than a quarter of one percentage point. This result is consistent with the finding in Lowe and Ellis (1997), in the context of optimal policy, that moderate smoothing of interest rates does not substantially affect the variability of inflation and output.
While the results are not reported, when the standard deviation of quarterly interest rate changes was constrained to be less than 1.5 percentage points, the four-period ahead forecast horizon still yielded the lowest combined inflation and output variability, although longer forecast horizons almost performed as well in some cases. Similarly, reducing the variability of interest rates by imposing a partial adjustment process onto an efficient Taylor rule also gave the best results when the rule involved a four-period ahead horizon.
Finally, the relative weight on inflation in the central bank's reaction function also increases as policy becomes more forward looking, since the information about future inflation embodied in the output gap has already been exploited to some degree (de Brouwer and O'Regan 1997). But in the model used here, this does not imply that the weights on the output gap go to zero as the forecast horizon is extended. As the forecast horizon moves out to, say, four periods, efficient policy still reacts to the output gap.
3.2 The Effect of Various Expectations Formations Processes
In the exercise above, we focused on central bank behaviour, assuming that people other than policy-makers did not have model-consistent expectations. In this section, we shift the focus to the private sector, and show how moving from backward-looking expectations to model-consistent expectations in goods/services, labour and foreign exchange markets can affect outcomes. We use the underlying structure of the model outlined in de Brouwer and O'Regan (1997), but adapt part of it – specifically, consumer prices, wages and the exchange rate – to allow for expectations to be based on different information sets (Appendix B). At one extreme, expectations are assumed to be fully model-consistent, (and hence, people know the reaction function of the central bank), while, at the other extreme, expectations of the future are formed only on the basis of lags of the particular variable. It is useful to spell this out in more detail.
Since the central bank has a low but non-zero target for consumer price inflation, the steady-state inflation rate is positive. Long-run inflation is modelled as a mark-up over unit labour costs and import prices in domestic currency:
where p is the price level, ulc is unit labour costs, ip is import prices in domestic currency, and β1 is a parameter bounded between 0 and 1. As written, Equation (3a) states that adjustment to the long run is instantaneous, an assumption clearly rejected by the data (de Brouwer and Ericsson 1995). Accordingly, we modify Equation (3a) so that inflation adjusts gradually to its long-run mark-up:
where gap is actual output less potential (estimated as a linear trend) and a superscript e indicates a model-consistent expected value at time t.[8] Inflation this quarter depends on the mark-up over unit labour costs and import prices (the ‘inflation fundamentals’), but the transition path is also determined by expected inflation and the state of demand (Blake and Westaway 1996). Expected inflation is assumed to be model-consistent average expected inflation over the coming year when price and wage setters are explicitly forward looking, and is average quarterly inflation over the past year when they form their expectations solely on the basis of where inflation has been in the recent past. The response of the central bank to inflation and output is part of the model, and so when people have model-consistent inflation expectations they take this into account. If the central bank is not credible, in the sense that (some) people do not think the central bank will respond to inflation shocks, then we assume that those people's expectations of inflation are based on recent past inflation. If the central bank lacks credibility, people expect that shocks to inflation permanently affect inflation.
The mix of ‘forward’ and ‘backward’ price adjustment incorporated in Equation (3b) can be motivated by forward-looking optimising models which incorporate stickiness in price adjustment, due, for example, to staggered contracts (Taylor 1979, 1980) or non-continuous price setting (Calvo 1983); see Petursson (1995) and Cochrane (1995) for more recent applications. The mark-up increases when inflation expectations rise, because of convex costs of price adjustment.
The parameter β3 is the weight on model-consistent expectations, taking a value of 1 when expectations are fully model-consistent. In this case, inflation is characterised as:
When expectations are extrapolative, however, inflation is:
The adjustment path also depends on the state of demand in the economy, with inflationary pressure falling when demand is relatively weak. In the long run, when there is no output gap and adjustment is complete, Equation (3b) collapses to Equation (3a).
We use estimates of parameters from earlier work to calibrate the inflation equation. On the basis of de Brouwer and O'Regan (1997), we assume that the coefficient on unit labour costs, β1, is 0.7, and that the coefficient on the output gap, β4 , is 0.07. The error-correction coefficient, β2 , is set to 0.25. Since we are interested in the properties of the economic system as people's expectations become more model-consistent, we set β3 to 0 or 1 to model the extremes of extrapolative and model-consistent inflation expectations respectively.
Inflation is modelled as a mark-up on costs, and the first component of this is unit labour costs. We use the terms unit labour costs and wages interchangeably. De Brouwer and O'Regan (1997) assumed that wages growth depends on recent past inflation and the state of demand. When wages growth is a linearly homogeneous function of past inflation, real wages will tend to be maintained without explicitly including a real wage target: an inflation shock is passed onto wages since wages growth is simply a function of past inflation. When alternative expectations processes are used, however, the real wage has to be modelled explicitly.[9]
Accordingly, we assume that wages are set to preserve real purchasing power consistent with an equilibrium value:
where the superscript eqm denotes the equilibrium real wage that is consistent with the inflation process and target. In the simple model used here, the equilibrium real wage is derived from the inflation equation. Assuming that import prices in domestic currency grow at the same rate as domestic prices in the long run, Equation (3a) can be rewritten in terms of the real wage, which implies an equilibrium real wage of Δp /β1.
Equation (4a) can be rewritten as a dynamic process for real wage growth, with adjustment to the long run also depending on the state of demand in the economy:
Wage setters do not know current inflation, so they set nominal wage growth for the current
period with expected inflation in mind. If expectations are rational (that is,
model-consistent), then E(Δpt) is given by the expected value
of Equation (3c) at time t – 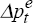 – which is simply
the inflation equation at time t without the inflation surprise. Since the inflation
equation contains future expected values of inflation, the wages process is also forward
looking. If expectations are extrapolations from the past, then
E(Δpt) is given by some average of past inflation rates,
which we assume to be average quarterly inflation over the past year,
– which is simply
the inflation equation at time t without the inflation surprise. Since the inflation
equation contains future expected values of inflation, the wages process is also forward
looking. If expectations are extrapolations from the past, then
E(Δpt) is given by some average of past inflation rates,
which we assume to be average quarterly inflation over the past year, 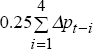 .
When there is a mix of model-consistent and extrapolative expectations, Equation (4b) becomes:
.
When there is a mix of model-consistent and extrapolative expectations, Equation (4b) becomes:
where γ3 is 1 when wage-setters' expectations are model-consistent and zero when they are extrapolative.[10] In the long run, when adjustment is complete and output is at potential, real wages equal their equilibrium value, regardless of the way in which expectations are formed. Real wage adjustment in Australia is typically a slow process, and so we assume a low speed of adjustment coefficient, with γ1 set to 0.1. Following de Brouwer and O'Regan (1997), we set γ2 to 0.17 (and so the labour market is more sensitive to excess demand pressures than is the mark-up in consumer prices).
Consumer prices are also a mark-up over import prices, which are affected by movements in world prices and the nominal exchange rate, with gradual, but eventually complete, pass-through (see Appendix B for the pass-through equation). World prices are assumed to be exogenous, but the exchange rate is not. While the nominal exchange rate is unpredictable in the near term, over longer periods of, say, quarters and years, it can be explained by inflation differences between countries, the terms of trade and the real short-term interest differential (Tarditi 1996).
We assume that the real exchange rate comprises forward-looking and backward-looking elements, in the form:
where an asterisk denotes a foreign variable, tot is the terms of trade, rtwi
is the real exchange rate in terms of domestic currency (so a rise is an appreciation), 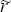 is the real
interest rate less the risk premium, and r is the real interest rate.[11]
If the foreign exchange market is forward looking, the real exchange rate is:
is the real
interest rate less the risk premium, and r is the real interest rate.[11]
If the foreign exchange market is forward looking, the real exchange rate is:
and appreciates when monetary policy is expected to be tighter or the terms of trade is expected to rise. This derivation is based on the uncovered interest parity condition (for example, see McKibbin and Sachs 1991). The more temporary is the expected movement in ‘fundamentals’, the smaller is the effect on the real exchange rate. If the equilibrium terms of trade rises, the real exchange rate moves immediately to its new equilibrium when expectations are fully forward looking, but temporary changes in the expected terms of trade have only temporary effects on the real exchange rate. In this formulation, the exchange rate is a jumping variable.
If the foreign exchange market uses only current and past information, then the real exchange rate is:
and responds to the most recent terms of trade and to current and lagged interest differentials. This formulation captures the empirical regularity that the exchange rate is highly responsive to the terms of trade and tends to appreciate steadily over time in response to tighter monetary policy (Gruen and Wilkinson 1991; Blundell-Wignall, Fahrer and Heath 1993; Tarditi 1996; de Brouwer and O'Regan 1997). Even in this scenario, the real exchange rate adjusts quickly, as is typical of asset prices in general. In the long run, the real exchange rate is determined by the terms of trade. The effect of different forward and backward-looking behaviour can be identified by shifting δ1 in Equation (5a) between 1 and zero. Since the real exchange rate also enters the output equation, it provides a link between the real cash rate, output and inflation.
We use the same data generating process for Australian output as de Brouwer and O'Regan (1997):
where y is non-farm output, y* is OECD output and fy is farm output (Appendix B). In the long run, Australian output is determined by foreign output, the terms of trade and the real exchange rate. Output falls below its long-run path when the real interest rate lies above the policy-neutral rate, which is the real rate when output is at potential and inflation is stable at the desired rate. Monetary policy affects activity over a period of time, but has no impact in the notional long run. Growth in farm output also has short-run effects on non-farm growth.
The data generating processes for foreign output, foreign prices, foreign real interest rates, farm output and the terms of trade are set out in Appendix B. The Fisher equation for the interest rate is:
where 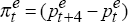 when
inflation expectations are forward looking, and
when
inflation expectations are forward looking, and 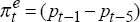 when they are
adaptive. We are implicitly assuming that it is the ex ante real interest rate which
matters to output and the exchange rate.
when they are
adaptive. We are implicitly assuming that it is the ex ante real interest rate which
matters to output and the exchange rate.
This stylised representation of the economy embodies a simple transmission process. The policy instrument is the nominal cash rate. Monetary policy reduces inflation by generating output gaps and an appreciation of the exchange rate. A rise in the nominal interest rate raises the real interest rate which affects output indirectly through the real exchange rate and directly through other mechanisms (Grenville 1995), generating downward pressure on wages and inflation. The appreciation of the nominal exchange rate, induced by higher local interest rates, also directly lowers inflation by reducing the Australian dollar price of imports. Given the lag structure of the model, the policy control lags for output are shorter than for inflation, and the initial effects of policy on inflation are through the exchange rate, with the output effects taking relatively longer.
To close the model we need to specify the way in which monetary policy is set. Since we are interested in assessing the properties of the system for different types of expectations formation, we characterise monetary policy as a four-period-ahead-forecast Taylor-type rule. We use arbitrary 0.5 weights on inflation deviations and the output gap in both cases.[12] While not shown here, the outcome that forward-looking policy does better than policy based only on currently available data follows when price setters are also explicitly forward looking.[13]
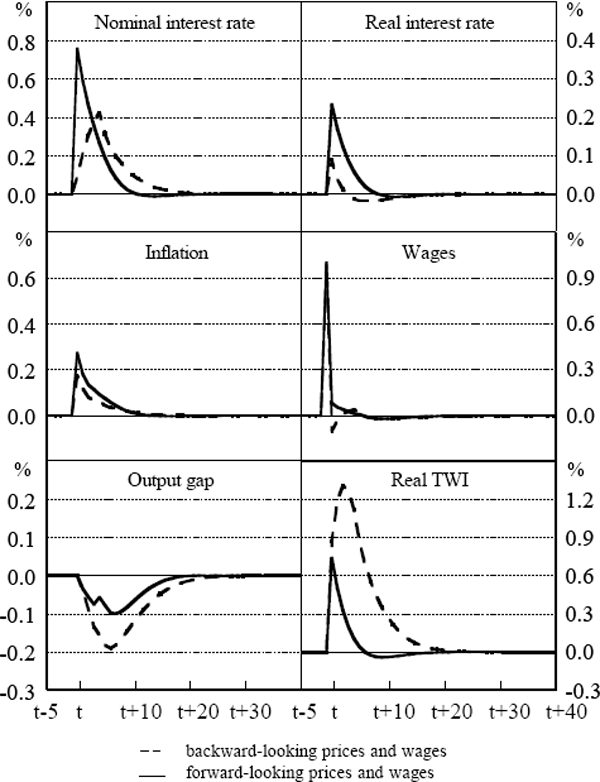
Figures 5 and 6 set out the effects on the nominal interest rate, the real interest rate (of price and wage setters), annual inflation, annual wages growth, the output gap and the real exchange rate of an unanticipated 1 per cent rise in wages at time t-1 when the foreign exchange market uses, respectively, current and past values or expected future values of fundamentals. Each figure shows the outcomes for model-consistent and extrapolative expectations in consumer price and wage inflation. The impulses are shown as deviations from baseline.
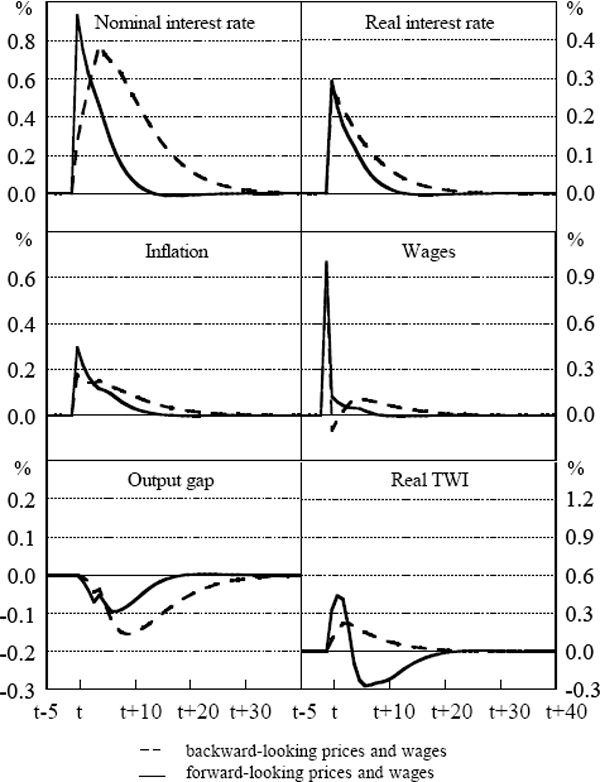
Consider the effect of a temporary rise in nominal wages growth when the foreign exchange market uses current and past, but not future expected, values of fundamentals (Figure 5). The real interest rate rises as soon as policy-makers are aware of the wages shock, since policy-makers increase the nominal rate. The effect of the shock on inflation dissipates only gradually. But the more model-consistent are expectations of prices and wages, the faster is adjustment to equilibrium, and the smaller is the deviation of inflation from target and output from potential. Explicit forward-looking behaviour tends to reduce the variability in the economic system caused by shocks.
The effect of the shock on the real exchange rate depends on the way expectations of consumer prices and wages are formed. If policy-makers use price and wage setters' inflation expectations in the Taylor-type rule, and if these inflation expectations differ to those of the foreign exchange market, then the real interest rates that affect output and the real exchange rate will be different from each other. For example, if the inflation expectations of the foreign exchange market are formed on the basis of lags of inflation but price and wage setters have model-consistent expectations (as for Figure 5), then the foreign exchange market's ex ante real interest rate will initially rise more than that of price and wage setters (since their inflation expectations have not risen as much), but it will then fall below neutral since their inflation expectations will tend to be rising while price and wage setters' inflation expectations – and hence, nominal interest rates – are falling. Consequently, the exchange rate tends to appreciate more initially, but then depreciates. In other words, the exchange rate oscillates in response to inflation (and other) shocks when inflation expectations are adaptive in the foreign exchange market but model-consistent in goods and labour markets.
The story changes somewhat when the foreign exchange market is fully forward looking (Figure 6). Since the exchange rate depends on current and future real interest rates, it jumps up in response to tighter expected monetary policy. Consider what happens when price and wage setters' expectations of inflation are formed on the basis of recent past inflation. In this case, the sum of the foreign exchange market's ex ante real interest rates – and hence, the jump in the exchange rate – is bigger than when price and wage setters have model-consistent inflation expectations.[14] This is a standard result in rational expectations models of the exchange rate, since the degree of overshooting is higher, the more sticky are prices in goods and labour markets (Dornbusch 1976). Given that the jump in the exchange rate is larger when the foreign exchange market is forward-looking but price and wage setters form their expectations only on the basis of what has happened in the past, the output gap is larger and the fall in import prices is greater, making the net inflationary impulse from the wages shock smaller than in the explicitly forward-looking case (for a given set of reaction coefficients in a simple rule). Note that the exchange rate does not oscillate in this case of bifurcated inflation expectations, but overshoots.
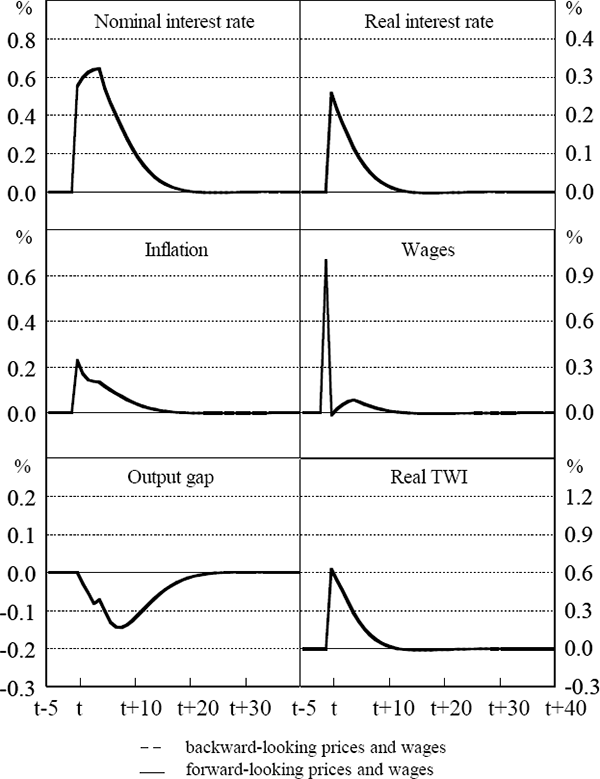
The assumption that goods, labour and foreign exchange markets are either fully ‘backward-looking’ or fully ‘forward looking’ is extreme. Consider, therefore, what happens when expectations draw on a mix of past and model-consistent values. Figure 7 shows the effect of a temporary wages shock when there is an arbitrary fifty-fifty mix of the two cases examined above. Since expectations are the same for all sectors, the system does not oscillate (since policy-makers are forward-looking) and there is only very moderate overshooting of the exchange rate. The inflation and output gap effects are, not surprisingly, an average of the other results. Under this particular policy rule, the nominal and real interest rates do not rise immediately to their respective peaks; there is some interest rate smoothing.
3.3 Optimal Policy
Given the basic underlying model and simple forward-looking policy reaction function, the way expectations are formed in goods and services, labour and foreign exchange markets matters to the way the economy responds to a shock to inflation (and implicitly to other variables in the system). The policy rule used in Section 3.2, however, is a simple feedback rule, and is neither efficient nor optimal. It is not efficient since the reaction weights (most probably) do not minimise the variability in inflation for a given variability in the output gap. And it is not optimal since it is only a simplification of the very complex rule that would result were the central bank to minimise its loss function, defined over forecasts of deviations of inflation from target and output from potential, subject to the equations that describe the economy.
The issue we examine in this section is whether policy-makers who set the instrument optimally can compensate for the lack of model-consistent behaviour elsewhere in the economy. In other words, are the inflation and output variability outcomes different for the various expectations processes when policy-makers set policy optimally, knowing what the expectations processes are?
To do this, we follow the characterisation of optimal policy outlined by Debelle and Stevens (1995) and Lowe and Ellis (1997). The central bank minimises a loss function – defined as deviations of forecast inflation from target, deviations of forecast output from potential, and the change in nominal interest rates – subject to the set of equations that describe the economy, to solve for a time path of its instrument, the nominal cash rate. This exercise is conducted every period, as new information is processed and forecasts are revised.[15] Clearly, the path of the nominal cash rate that is produced by this exercise depends on the model used, but we use it to demonstrate some features of optimal policy in the face of different expectations processes.
The loss function is given as:
where f denotes the current forecast of the relevant variable. The larger is ω, the more the central bank wants to smooth interest rates. We assume that ω is 0.1 (Lowe and Ellis 1997). While this number affects the inflation/output variabilities in absolute terms, it does not affect the relative outcomes. The parameter λ is the weight on deviations of output from potential in the loss function, and is zero if the central bank is only concerned with stabilising inflation around the target.
We assume that price/wage inflation expectations and foreign exchange markets are either fully explicitly forward-looking or are keyed only off past values, yielding four possible scenarios. We assess the outcomes for the same set of shocks in order to directly compare the variance properties of the system for different expectations processes, but we readily acknowledge that the ‘true’ errors would most likely be different under each representation. Figure 8 shows the different outcomes for the variability of inflation and output for each of these scenarios using different weights on inflation and output in the objective function.
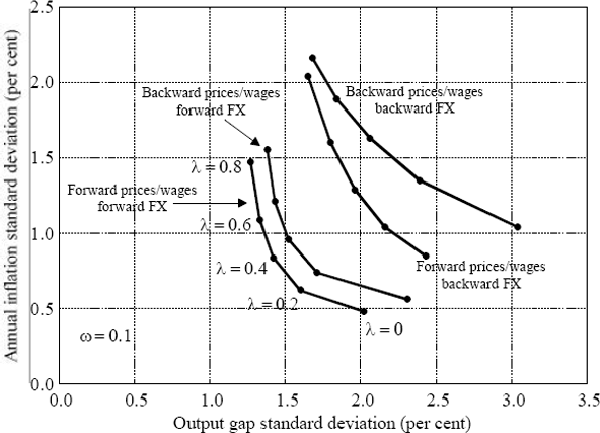
Figure 8 has three distinguishing features. The first is that the optimal policy outcomes differ depending on the expectations processes of other groups in the economy: the ‘best’ that policy-makers can do to reduce the variability in inflation and output depends on the structure of the economy that they have to work with. Policy-makers can reduce the variability in inflation and output most when goods, labour and foreign exchange markets are all forward-looking with model-consistent expectations, and least when markets form their expectations about the future only using past information. When people have model-consistent expectations, they know that shocks affect policy-makers' forecasts of the economic system, and they adapt their behaviour accordingly. They know, for example, that policy will respond to an inflation shock, and so they change their forecasts.
Second, the schedule which traces out the optimal outcomes becomes more convex the more explicitly forward-looking is behaviour. In other words, the reduction in the variability in inflation comes at a smaller cost to increased output variability. In this model, for example, when people focus only on the past, the 1 percentage point reduction in the standard deviation of inflation that is achieved by putting maximum weight on inflation in the objective function costs about a 1¼ percentage point rise in output variability. But when people form expectations based on the model of the economy, including how the central bank behaves, this cost is reduced to ¾ percentage point.
Stabilisation policy is enhanced if people take account of the way the economy works – including the fact that the central bank reacts to inflation – when they form their expectations about the future. This is perhaps one reason why many central banks in developed countries have adopted explicit inflation targets. Such targets focus people's attention on the future and are a strong statement that central banks are serious about maintaining low and stable inflation. In turn, this provides people with information about the likely path of inflation in the future, and helps to anchor inflation expectations to the inflation target. It also underscores why central banks have placed particular emphasis on establishing the credibility of their inflation target regimes.
The third feature is that there is a notable difference between outcomes when, on the one hand, inflation expectations in goods and labour markets are model-consistent but those in the foreign exchange market are backward looking, and when, on the other, inflation expectations in goods and labour markets are backward-looking but those in the foreign exchange market are model-consistent. In other words, the way in which expectations processes differ between markets matters. The system in which the foreign exchange market is model-consistent, and price and wage setters are not, yields the better outcome. The explanation is twofold. First, the exchange rate appreciates more in response to inflation shocks when inflation expectations in the foreign exchange market are model-consistent, thereby lowering the variability in inflation. Second, inflation expectations in the foreign exchange market which are extrapolations of past inflation generate cycles in the real exchange rate and, therefore, output and inflation, which induces more variability in inflation and output.
What is not evident from Figure 8 is what happens to the variability of the instrument, the nominal cash rate. The variability of changes in the cash rate falls substantially as expectations become more model-consistent. For example, when expectations of the future are based only on recent history, the standard deviation of changes in the cash rate is 2.5 per cent, but it is 0.3 per cent when expectations are all model-consistent (for a weight of one on inflation in the objective function). Implicitly, policy needs to be less activist when people are explicitly forward-looking and the central bank is credible.
Footnotes
Since output and inflation are influenced by the real interest rate, we assume that policymakers set the nominal interest rate to achieve the desired real interest rate. Accordingly, in Equations (2a) and (2b), the expected annual inflation rate used to define the real interest rate can be different from the inflation rate to which policy-makers respond. This also allows us to show the impact that heterogeneous private-sector inflation expectations can have on economic outcomes in the next section of the paper. [5]
Policy-makers use structural, model-based forecasts of inflation, and so the system is not subject to the indeterminacy problem that arises when policy-makers use inflation forecasts which are set equal to the inflation target (Bernanke and Woodford 1997). [6]
We use the first 200 of the 1,000 shocks in de Brouwer and O'Regan (1997). The properties of the shocks are outlined in Appendix B. Since we use a smaller number of shocks, our sample means are more likely to deviate from the population means, and so we evaluate variabilities around the population mean, rather than the sample mean. For example, variability of the output gap is assessed around zero, while variability of annual inflation is assessed around 2.5. The simulations were constructed by solving simultaneously for the endogenous variables over a 25-period horizon. At each point in time, the system is solved assuming exogenous and endogenous variables take their expected values, based on the known data-generating processes. To close the model, annual inflation is assumed to be 2.5 per cent and output is assumed to be at potential beyond the 25-period horizon (which is sufficiently far in the future in an adaptive model to not affect current outcomes). The realisations for the current period are determined by applying the current set of shocks to these solutions. These realisations become part of the historical starting values for the forecast horizon beginning in the following period. [7]
The coefficients on the mark-up and leads and lags of inflation sum to unity in order to ensure that inflation equals the expression for inflation in Equation (3a) in the long run. The leads and lags of inflation are multiplied by 0.25 since inflation depends on the average lead or lag (and so if we used eight leads or lags, the second term would be multiplied by 0.125). [8]
If there is no explicit real wage targeting by wage setters, such that nominal wages depend only on future expected inflation, then real wages will fall when there is an unanticipated rise in inflation. [9]
This specification assumes that wage contracts are written only for the current quarter. If contracts are longer and if expectations are forward looking, then longer leads of inflation will enter the equation. While we do not report the results of extending wage contracts, the effect is to lengthen the adjustment process. The qualitative results of the analysis in Section 3.2 and 3.3 are unaffected. [10]
For the purposes of this model, we assume that the neutral real rate for Australia is 3.5, which is higher than the average world real interest rate since 1980. We call the difference between 3.5 and the world average real rate the risk premium. Implicitly, a rise in the risk premium induces a depreciation of the Australian dollar. [11]
While the 0.5 weights were used by Taylor, other work has shown that this weighting is probably neither efficient nor optimal (Bryant, Hooper and Mann 1993; Black, Macklem and Rose 1997; de Brouwer and O'Regan 1997). [12]
We assume that policy-makers use the inflation expectations of price and wage setters to set the nominal interest rate. [13]
The foreign exchange market's ex ante real interest rate initially falls, since their inflation expectations are initially higher than those of the backward-looking price and wage setters, but this is later reversed, with the net effect a rise in the real interest rate differential. [14]
A Lagrangean was derived from the loss function expressed over the period t = 0 to t = 40 , with the constraints being the behavioural equations for the endogenous variables in each period. This expression was differentiated with respect to the policy variable (nominal interest rates) and endogenous variables at each point in time, and the corresponding Lagrange multipliers. The result is a system of 861 linear equations with algebraic terms for exogenous, endogenous and policy variables. The optimal path of interest rates is obtained by solving this system simultaneously for the interest rate, endogenous variables and Lagrange multipliers, given that the exogenous variables take their expected values. As in the Taylor-rule case, the actual realisation for the current period becomes part of the set of starting values for the next iteration. The exercise is repeated 200 times, using the first 200 shocks from de Brouwer and O'Regan (1997). [15]