RDP 9409: Default Risk and Derivatives: An Empirical Analysis of Bilateral Netting 3. Credit Exposure
December 1994
- Download the Paper 105KB
The credit risk of swaps relates only to the cash flows exchanged by the counterparties and does not involve the underlying notional principal. Credit risk on these instruments arises only when a counterparty defaults and interest rates have changed such that the bank can arrange a new swap only at inferior terms. Default alone, therefore, does not expose the bank to loss. In the absence of a change in interest rates the bank could negotiate a new swap on the same terms as the old swap. If interest rates do change, however, it may not be possible to replace the swap on comparable terms. In such cases, the bank may experience a loss relative to its position had the counterparty not defaulted. The size of this loss will depend on the interest rate environment at the time of default and cannot be perfectly foreseen.
3.1 Credit Exposure at a Point in Time
The basic concept used in this study to measure credit exposure, for a single swap, is replacement cost. This method estimates the economic impact on the bank from default of a counterparty as a function of the original contract fixed rate and the market rate that would be used when finding a substitute counterparty. Replacement cost is calculated as the difference between the fixed rate of interest of the swap and the market rate, discounted back from each settlement date to the revaluation date. This approach assumes that the bank closes out its exposure arising from a defaulting swap by writing a replacement swap (the approach, which focuses on the fixed rate side of swap transactions, assumes that the loss in replacing the floating rate side of a swap will be minimal).
To value a swap a standard zero coupon methodology is used. Zero coupon rates are pure discount interest rates for securities with no intermediate coupons (that is they repay interest and principal in one payment at maturity). This method overcomes the weakness of traditional internal rate of return calculations in which cash flows of varying maturities are revalued using a single interest rate. Par yield structures implicitly assume that all coupons or intermediate cash flows are invested at the same yield to maturity.[4] In contrast zero coupon rates do not involve reinvestment risk. Zero coupon methodology allows the identification of a discount rate appropriate to the timing of each cash flow.[5]
By way of example, consider a 4-year swap which was entered into on 30 September 1990 with a fixed rate of 14 per cent per annum payable semi-annually. The bank receives the fixed rate from its counterparty in exchange for paying some floating rate. The transaction is for a notional principal of $20 million. Assuming that on 30 September 1992 the market swap rate (that is, the fixed rate the bank would receive if it entered into a swap on 30 September 1992) has moved to 10 per cent and that the zero yield curve is as shown in Table 1, the bank's exposure to its counterparty on that date may be calculated as follows:
| Date |
Payment due to bank | Payment bank receives under replacement swap | Difference |
Zero rate | Present value |
|---|---|---|---|---|---|
| 30 Sep 92 | 1,400,000 | 1,000,000 | 400,000 | – | 400,000 |
| 30 Mar 93 | 1,400,000 | 1,000,000 | 400,000 | 5.00 | 390,438 |
| 30 Sep 93 | 1,400,000 | 1,000,000 | 400,000 | 5.50 | 379,147 |
| 30 Mar 94 | 1,400,000 | 1,000,000 | 400,000 | 5.85 | 367,388 |
| 30 Sep 94 | 1,400,000 | 1,000,000 | 400,000 | 6.25 | 354,325 |
| Total: | 1,891,299 | ||||
The first column in Table 1 sets out the remaining coupon payment dates on the original swap. The payment due to the bank each six months on that swap is 0.14 × $20 million / 2 = $1,400,000. Similarly the payment receivable under the replacement swap is 0.10 × $20 million / 2 = $1 million. Hence, in the event that the counterparty defaults, the bank would, at each coupon payment date, receive $400,000 less than if the counterparty continued to meet its obligations. Assuming a zero yield curve as shown in Table 1 the present value of this lost income stream is $1,891,299.
Note that credit risk is not symmetric. If the counterparty defaulted when interest rates had risen to, say 16 per cent, then the bank would be able to replace the contract at a profit. In such a case the credit exposure on the contract is nil.
3.2 Credit Exposure Over Time
Calculating the current credit exposure on an interest rate swap or an FRA is relatively straightforward. Complexity arises in the calculation of future or potential exposure, however, because the value at risk changes over time as interest rates change. Frye (1992) and Simons (1993) set out a methodology for the estimation of future exposure. This begins with an interest rate model which is used to predict future interest rate paths. From the interest rate model, a confidence interval (say 95 per cent) is taken to yield the “worst case” upward and downward movements in interest rates. Figure 2 provides an illustration of the projections from a simple model. The interest rate model used for the simulations presented in this paper is set out in Appendix 1.
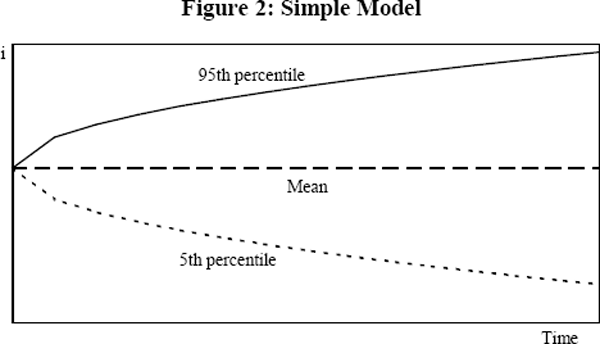
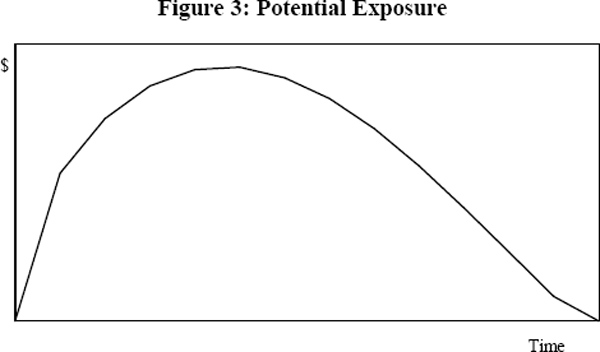
The swap is then revalued from the current date forward, through to its maturity using the projected worst case interest rates. This gives the potential exposure for any future date. Figure 3 shows the theoretical time path of potential exposure for a standard swap. Two factors affect the potential exposure. Firstly, the potential in-the-money amount which moves directly with interest rates. And secondly, the total coupon amount outstanding which declines each time a coupon payment is made.
3.3 Counterparty Exposure
Once the credit exposure for individual contracts has been calculated, the next step is to calculate the exposure to a counterparty that has several swaps and FRAs in force. This is a three-step process:
- Calculate the potential exposure time path for each contract.
- Combine the potential exposures of all contracts, at each point in time, to arrive at the total exposure to the counterparty over time. The way in which the contracts are combined depends upon whether the contracts can be netted. In the case that netting is applicable, the contract values, at each date, can simply be summed. In the absence of netting, exposure to a counterparty is assessed as the sum of the replacement cost of all contracts that are in the money (that is, all contracts wherein the counterparty owes the bank money, or those contracts that would be replaced in the market at a cost to the bank). The exposure on out-of-the-money contracts is zero.
- Credit exposure at each point in time is taken to be equal to the maximum exposure obtained under each of the various interest rate scenarios to obtain a time path for worst case losses.[6] To collapse these time paths into a single credit exposure number the maximum exposure is taken. Choosing the maximum exposure assumes that the counterparty will default at the worst possible time. Alternatively, average exposure over time may be calculated. Use of the average measure assumes that the counterparty is equally likely to default at any time between now and the maturity of the contract.[7]
In determining the exposure to a counterparty, assumptions must be made about the composition of the portfolio through time. The simplest approach (and the one used in the calculations set out below) is to assume that the portfolio remains static. The difficulty with this is that as the portfolio ages, contracts mature and drop out of the portfolio. An alternative approach is to assume some pattern whereby the portfolio is replenished over time. Not allowing for new contracts to be entered into over the life of the portfolio, means that exposure to many counterparties is underestimated. However, imposing arbitrary assumptions about the evolution of the portfolio is also problematical and can lead to errors in estimating exposure.
Footnotes
Most traded securities are not zero coupon securities but rather involve both a final principal payment and regular coupon payments. The par yield is that yield for such securities commonly observed in the market. [4]
For a full exposition of the zero coupon methodology see Das (1994). [5]
This eliminates one set of mutually exclusive events; reflecting the fact that interest rates cannot be at both the upper and lower bounds of their confidence interval at the same time. An alternative approach would be to constrain the speed of shifts in the yield curve, for example, setting a rule that the 3-year rate cannot move by more than a set amount in two years, and divide events accordingly. This can have the effect of reducing estimated counterparty exposure, on a bank's total portfolio by as much as 40 per cent. [6]
In theory it is possible to specify the expected probability that a counterparty will fail at any given time (for example, it may be unlikely that the counterparty will default in the next year, but more likely that it will fail in two year's time) and so calculate a probability weighted expected exposure. [7]