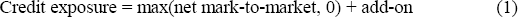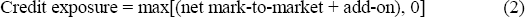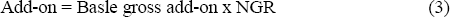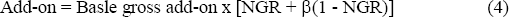RDP 9409: Default Risk and Derivatives: An Empirical Analysis of Bilateral Netting 5. Capital Standards
December 1994
- Download the Paper 105KB
5.1 The Current Capital Requirements
For the purposes of capital adequacy the credit risk of financial derivative transactions is divided into two parts.[9] Firstly current exposure, which captures the loss that would result if a counterparty were to default today. This is measured as the mark-to-market valuation of all contracts with a positive replacement cost. Secondly, since the value at risk from counterparty default changes over time, an allowance for changes in the value at risk, in the event of default, is calculated for all contracts.
The add-on for potential exposure is calculated as a percentage of the nominal principal amount of each contract. The factors to be applied are set out in Table 5.
| Remaining term to maturity | Interest rate contracts % |
Exchange rate contracts % |
|---|---|---|
| Less than one year | nil | 1.0 |
| One year or longer | 0.5 | 5.0 |
Counterparty weights (10 per cent for State and Commonwealth Governments, 20 per cent for Australian and OECD public sector entities and banks, and 50 per cent otherwise) and the 8 per cent capital charge are then applied to the value at risk to determine the level of capital to be held against derivative transactions. For further details see Reserve Bank of Australia (1990).
5.2 The Basle Committee's Proposal on Netting
The proposal on netting sets out the minimum legal requirements for netting to be recognised for the purpose of capital adequacy and the calculation of credit risk for those jurisdictions where netting is legally enforceable. Current exposure will be calculated on a net basis to produce a single credit or debit position for each counterparty. With regard to the add-ons for potential exposure, however, the proposal recommends the maintenance of the existing calculation method.
5.3 Formulating a Capital Charge
While it is important to maintain a suitably conservative and easy-to-understand capital standard, it is possible there may be more efficient methods of capturing credit exposure than the proposed method. Determining an appropriate approach requires choosing a method which covers exposure under all likely circumstances and one that does so with an efficient allocation of capital. That is, the capital charge should be based on a variable that is reasonably strongly correlated with a portfolio's exposure.
Three issues arise in formulating a more efficient capital charge:
- whether only current exposure needs to be covered, or add-ons should also be applied to allow for potential exposure;
- how to better express total credit exposure as a function of the gross and/or net market values; and
- how to calculate the add-on itself.
5.3.1 Why Have Add-Ons?
The need for add-ons flows directly from the fact that the value of derivative portfolios is volatile. The mark-to-market value of a portfolio only captures current exposure. The net market value of contracts can change significantly over a relatively short time. A capital charge must provide a margin of safety to ensure that sufficient capital is held not only to cover current exposure but also to cover potential exposure.
In general, the probabilities of credit exposure either increasing or decreasing are about equal. Thus the average change in credit exposure will be small. However, this does not imply that there is no need for add-ons. Without an add-on the capital charge will cover actual exposure only in those cases where net replacement cost does not increase. A capital charge that provides adequate coverage only half of the time is not providing a very good margin of safety. To provide better coverage an add-on is required.
5.3.2 Total Credit Exposure
The Basle Committee's proposed method calculates credit exposure as being equal to the sum of net mark-to-market, if positive, plus the add-on. That is:
There is a difficulty, however, with this construct. Regardless of how negative the net mark-to-market value of the portfolio, a bank is still required to hold capital against the full amount of the add-on. Thus, for two otherwise identical portfolios, one which has a positive current net replacement value must have a higher potential future replacement value than one with a negative current value.
By way of example, consider the three hypothetical contracts depicted in Figure 2. The figure shows the current value of the three contacts and the values these contracts would take over time under worst case interest rate movements.
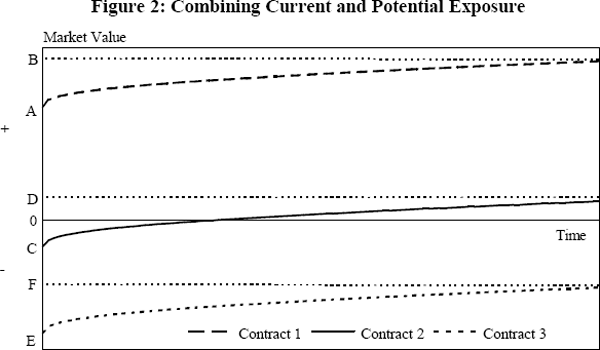
For contract 1, which currently has positive value (and hence, positive credit risk) the maximum loss is equal to B. Assuming the add-on covered the increase in value over the life of the contract (B − A) then the current netting proposal calculates credit exposure as A + (B − A) = B, which is the correct amount. In the case of contract 2, however, the maximum loss in the event of counterparty default is equal to D. The Basle proposal would calculate credit exposure as being equal to the distance between C and D, since current exposure is set equal to zero. This overstates total credit exposure by the amount C. In the most extreme case, contract 3, the contract is so far out-of-the-money that it is not expected ever to take on a positive value. In this case there is no credit risk, but the bank would still be required to hold capital against the amount (F − E).
One option, presented in Gumerlock (1993) which would correct this distortion would be to recast the measure of credit exposure along the following lines:
That is, credit exposure for each counterparty is calculated as the sum of the net mark-to-market and the add-on, if this sum is positive, and zero otherwise. Using this formula would ensure that capital is not required to be held against contracts that would not be subject to credit risk even under the worst-case movement in underlying interest rates.
A quite different approach to estimating total exposure, which also makes an allowance for the volatility in the value of swap contracts as market rates change, is to adopt a form of scenario analysis. Under such an approach, total credit exposure, for each counterparty, could be calculated as the maximum, if positive, value of all contracts under various interest rate scenarios. For example:
- current rates;
- interest rates rise by a given amount; and
- interest rates fall by a given amount.
For the purposes of this exercise, upward and downward shifts in the yield curve of one per cent have been applied and tested.
5.3.3 Add-Ons
There have been a range of suggestions as to how, in a netting environment, an add-on for potential exposure could be formulated.
Market participants argued, initially, for an add-on calculated as a proportion of the net replacement cost of the portfolio where net replacement cost is defined as the market value of the portfolio if positive and zero otherwise. There is, however, one fundamental shortcoming in using the net mark-to-market value as a base for an add-on. Where the net mark-to-market value was zero, there would, by definition, be no add-on and thus no coverage for potential exposure. There is no reason to expect that portfolios with a zero net mark-to-market do not have the potential to increase in value, though, across a total portfolio containing a reasonably large number of counterparties this effect may not be empirically important.
Hendricks (1992) and Estrella (1992) investigate the performance of net replacement cost as a base for a capital charge, in comparison with notional principal. As stated previously, the potential credit exposure of a derivative instrument is a function of the variance of the net replacement cost of that instrument. Hence, some insight may be gained into the appropriate base by investigating the relationship between the variance of the market value of swap contracts and the notional principal and between the variance and the net replacement cost.
Estrella (1992) sets out the mathematical functional form for the potential exposure of an interest rate swap by defining potential exposure as being directly proportional to the standard deviation of the market value of a swap. Estrella substitutes a general model of interest rates into an equation specifying the value of a swap (a simplified version of equation (A5) discussed in Appendix 1). This enables changes in the value of the swap to be decomposed into a deterministic and a random component, from which, an expression for the standard deviation, and therefore, the potential exposure of the swap value is obtained.
The functional form of the expression for potential exposure obtained by Estrella demonstrates that potential exposure is a rising function of notional principal. However, the relation between potential exposure and net replacement cost may be positive or negative, and therefore, of itself the relation is not informative.
Further simulation work conducted by Hendricks (1992) tested how well add-ons based on notional principal and net replacement value covered potential exposure as the proportion of the portfolio being netted increases. An add-on calculated as 35 per cent of net replacement cost provided adequate cover both in the absence of netting and when a small proportion of the portfolio is netted. As the proportion of the portfolio being netted increased the coverage afforded by the add-on based on net replacement cost fell significantly. If the weight applied to net mark-to-market was set so as to provide adequate coverage in all cases it would be quite high (for Hendricks' portfolio the figure of 35 per cent increased to around 900 per cent of the net mark-to-market value). The add-on based on gross notional principal provided a level of cover which varied much less as the proportion of the portfolio being netted changes. It provided adequate cover independent of the extent of netting.
An alternative to an add-on set as a simple proportion of net mark-to-market is to express potential exposure as a more complex function of gross and net values. For instance, the International Swap Dealers' Association (ISDA) has suggested scaling the existing add-ons by the ratio of net to gross market values. Here, net is defined as the higher of the difference between the positive market values minus the negative market values and zero. Gross is set equal to the sum of the market values of all positive valued contracts. The net to gross ratio is one measure of the extent of offsetting contracts within a portfolio. So long as the values of the contracts in a portfolio exhibit some degree of correlation, netting can be expected to reduce potential exposure. The greater the number of offsetting contracts the greater the reduction in potential exposure. Thus an add-on can be cast in the form:
where the Basle gross add-on is calculated as a proportion of the nominal principal amount (as set out in Section 5.1) and NGR is the ratio of the net mark-to-market to gross mark-to-market. The difficulty with this construction, as in the more simple add-on based solely on the net mark-to-market value, is that when the net mark-to-market is zero, no capital is held. Unless the contracts are perfectly correlated and perfectly offsetting, this will not be an adequate measure of potential exposure.
To retain the same general approach, but ensure a minimum level of capital is held when the net mark-to-market is zero, the add-on can be expressed alternatively as:
where β is a constant between 0 and 1. The level of minimum coverage, when the net mark-to-market is zero, would be set by appropriate choice of β.
However, there are some difficulties with the conventional definition of the net-to-gross ratio as it appears in both equations (3) and (4).[10] Consider the two portfolios presented in Table 6 (below). The first portfolio is out-of-the-money. The net to gross ratio, therefore, is zero. For an add-on of the form (3) it is implicitly assumed that portfolios that are out-of-the-money will not increase in value in the future. This is inappropriate. The object of calculating an add-on is to provide for potential increases in the value at risk and this should be done for all counterparties, not just those with a net positive market value. The ISDA ratio is also inappropriate when using (4), as this would assume that all out-of-the-money portfolios could be expected to increase in value by the same amount. Taking the absolute value of the net mark-to-market when calculating the net to gross ratio is one method of overcoming this problem.
| Portfolio | 1 | 2 |
|---|---|---|
| −15 | −3 | |
| −20 | −5 | |
| Contract market values | −2 | −5 |
| 10 | −7 | |
| 18 | −8 | |
| Net mark-to-market | 0 | 0 |
| Gross value | 28 | 0 |
| NGR | 0 | ? |
| Absolute ratio | 9/65 = 0.1385 | 1 |
For the second portfolio which contains only contracts that are out-of-the-money, the gross mark-to-market is equal to zero. Hence, the net-to-gross ratio is undefined. Since all the contracts are on one side of the market, intuitively, the net-to-gross ratio should be set equal to one. Replacing the ISDA ratio with the ratio of the absolute value of the net mark-to-market to the sum of the absolute market value of each contract, which we term the absolute ratio, achieves this.[11]
Another approach is one that relaxes the assumption, implicit in the Basle Committee's proposed method of calculating add-ons, that at the time a counterparty defaults there has been a worst case movement in the underlying rates of all contracts. This approach begins with the observation that the contracts that make up a portfolio can be divided into short and long contracts. Short contracts are those that increase in value as interest rates rise, while long contracts are those that increase in value as interest rates fall.
Consider a matched pair of offsetting contracts. At any point in time only one of these contracts, either the short or the long contract, will be in-the-money and hence carrying credit risk. The Basle method requires that an add-on be charged against both contracts. For both contracts to be in-the-money would require the one underlying market rate to be at two different levels at the same time.
More generally, within any portfolio (whether perfectly matched or not) for any given shift in swap interest rates the credit risk on either the short or the long contracts will increase. Thus potential exposure is limited to the maximum of potential exposure on the short contracts and the potential exposure on the long contracts. This could be reflected by setting a capital charge which takes the maximum of the add-ons on all short contracts and the add-ons on all long contracts.[12]
The assumption implicit in the Basle add-ons of simultaneous worst case movements in the underlying rates of all contracts is equivalent to assuming that there is no correlation between the prices of any contracts. Levonian (1994) demonstrates that taking the maximum of short and long add-ons represents a halfway case which is appropriate when there is some correlation, but not perfect correlation between contracts.[13] From Levonian (1994) it follows that the absolute value of the difference between the short and long add-ons (termed the net of short and long add-ons) is appropriate in the case that there is perfect correlation between contract values. Levonian (1994) suggests a generalisation of the short/long approach, namely taking a weighted average of the gross and net measures. The higher the correlation between contracts the greater the relative weight on the net amount.[14] All three measures discussed here were tested.
An approximation of the short/long approach which requires slightly less information is to split the portfolio between positively and negatively valued contracts. If the interest rate cycle is relatively smooth and the average maturity of the bank's portfolio is short then the positive/negative approach will provide a reasonably close approximation of the short/long add-ons. As in the short/long case we tested three means of combining the add-ons on positively and negatively valued contracts – the maximum, the absolute value of the difference between the add-ons on positively and negatively valued contracts (that is the net add-on) and a weighted average of the gross (that is, the current Basle add-ons) and the net add-ons.
Yet another approach to the determination of a capital charge derives from the fact that two perfectly correlated contracts, on opposite sides of the market, will have a zero potential exposure in a netting environment; as movements in the price of the positively valued contract will always be offset by the negatively valued contract. Thus, for contracts that are highly correlated, there may be a case for allowing add-ons to be netted.
One means of doing this would be to apply a broader range of factors to calculate add-ons than the four factors currently specified in the capital adequacy guidelines.[15] For example, time bands could be established for both interest rate and exchange rate contracts of differing maturities. This would allow long and short contracts of like maturity, and similar pricing behaviour, to be grouped and netted against each other.
To test that approach, interest rate contracts were divided up into the time bands shown in Table 7. The bands were set to roughly correspond with the general risk weights specified in Basle's proposal covering market risk on traded debt instruments.[16]
| Remaining term to maturity (years) | Per cent |
|---|---|
| term < 1 | 0 |
| 1 ≤ term < 2 | 0.2 |
| 2 ≤ term < 3 | 0.3 |
| 3 ≤ term < 4 | 0.4 |
| 4 ≤ term < 5 | 0.5 |
| 5 ≤ term < 7 | 0.6 |
| 7 ≤ term < 10 | 0.7 |
| 10 ≤ term < 15 | 0.8 |
| 15 ≤ term < 20 | 0.9 |
| term ≥ 20 | 1 |
A final approach is one that extends the time bands approach. Rather than increasing the weight on notional principal in discrete steps, the potential exposure add-on is specified as a smooth, linear function of the term to maturity.
That is the add-on can be expressed as:
where:
| t | denotes the remaining term to maturity; and |
| FV | denotes the notional principal amount of the contract. |
The scaling factor of 4.5 per cent was chosen to approximate the time band weights set out in Table 7. The weights applied to the notional face value of interest rate contracts under this, linear approach, the current Basle method and the time bands method are shown in Figure 3.
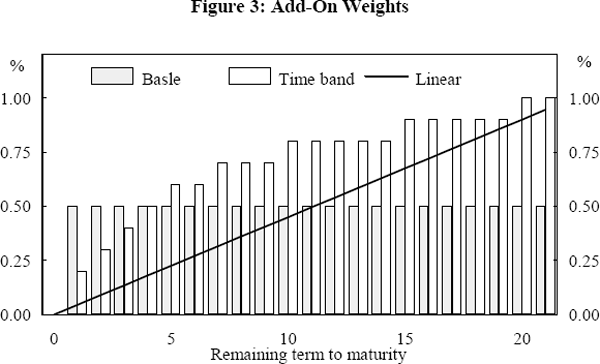
The rationale behind the linear approach is that the volatility of the value of interest rate contracts increases smoothly and continually as the term to maturity lengthens rather than in discrete jumps. Therefore, a linear function may provide a better approximation of the true pattern of price volatility than a step function.
As is the case with the time band approach, the add-ons can be calculated either on a net or gross basis. For the linear method, we net across all contracts with a counterparty regardless of maturity. Given that the correlation even between the yields on six month and ten year swaps is quite high (refer Table 3) there is some justification for netting across all contracts. This overcomes a weakness of the time band approach – the capital required to cover potential exposure can increase sharply when closely, but not perfectly, matched contracts fall into separate time bands.
In addition to looking at the gross and net add-ons under the linear approach we combine the linear approach with the short/long approach. That is the maximum and a weighted average of the add-ons (calculated using equation (5)) on short and long contracts are also tested in the following sections.
Footnotes
The following discussion summarises the current exposure method of determining credit risk. A simpler approach, the original exposure method, is available to banks which simply sets total credit exposure equal to a proportion of notional face value according to whether the contract is an interest rate of foreign exchange derivative and the total term to maturity of the contract. As at December 1993, all Australian banks, except two, employed the current exposure method. Both banks using the original exposure method were moving towards adopting the current exposure method. [9]
Net here is defined as zero when the difference between the positive and negative market values is zero. [10]
Moving from the conventional definition of the net-to-gross ratio to the absolute ratio leads to a slight increase in the amount of capital required. However, this can be offset by an adjustment of the weights set out in Table 5. [11]
For more complex portfolios splitting the portfolio up into shorts and longs is not necessarily straightforward. For example, a portfolio of foreign exchange swaps is exposed to movements in, at least, three underlying markets, namely, interest rates in each currency and the exchange rate. Hence it is possible to describe short and long positions in each of those underlying markets. The simplest solution is to treat the contract as though it is only exposed to the most variable factor (in this example, the exchange rate). It is then possible to take the maximum of short and longs in each product category (interest rate, foreign exchange, equity derivatives etc.) and sum the results across all product categories. However, this ignores any correlation between interest rates, exchange rates, equity prices and other asset prices. [12]
Levonian (1994) analyses the market risk embodied in a foreign exchange portfolio. This analysis can be applied here by noting that the short and long foreign exchange positions in Levonian's discussion are analogous to the add-ons on all short contracts and the add-ons on all long contracts in our credit risk analysis. [13]
As a practical matter one difficulty with the weighted approach is that the optimal weights tend to vary over time. Hence the weights and banks' systems for monitoring capital adequacy would need to be updated frequently. [14]
See Section 5.1. [15]
Basle Committee on Banking Supervision (1993), Annex 2. [16]