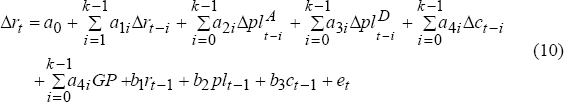RDP 9407: Explaining Import Price Inflation: A Recent History of Second Stage Pass-through 6. Estimating the Second Stage of Price Adjustment
December 1994
- Download the Paper 106KB
Given that, at the first stage, pass-through of changes in the exchange rate is completed rapidly, of special interest is the nature of price adjustment at the second stage, as import prices over the docks are passed on to those at retail outlets. Here, our priors are for a significantly different profile of adjustment. To estimate second stage pass-through we commence with the following levels expression:
where PL = P × T and does not explicitly include a measure of so that the retail price of an import is a function of the tariff-adjusted or landed price of the import and other domestic costs faced by the retailer.[27]
This levels expression is equivalent to equation (4) except that it does not constrain π to equal (1 − α), and does not explicitly include a measure of the mark-up. Instead, in this empirical section, we work from the premise that the mark-up on costs is constant in the long run and so is represented by the constant term, δ. Thus equation (9) describes a long-run relationship.
In the short run, however, we expect that the mark-up may vary and be an important explanator of retail import prices. Variation in the mark-up will be evident if short-run coefficients on PL and C are less than their corresponding long-run coefficients. In fact, it will be especially evident if short-run coefficients also display asymmetry in the response of the retail price to changes in these explanators. However, in addition to the role played by changes in PL and C in the short-run dynamics, we consider a role for those factors that, a priori, we expect to be related to the behaviour of the mark-up. One such factor is the output gap.
We consider a role for the output gap because when actual demand exceeds potential, and markets are imperfectly competitive, firms can increase their mark-up with little fear of loss of customers (Benabou 1992).[28] We also consider the possibility that, in the short run, the retail import price responds differently to changes in the landed import price during episodes of appreciation compared with depreciations (PSA 1989).
Again, we shall use an UECM to isolate the long-run relationship between the variables from their behaviour in the short run. An equation of the following general form is estimated:
where GP is the level of the output gap and superscripts A and D denote episodes of appreciation and depreciation, respectively. As previously, variables expressed in lower case are logarithms. The results of this estimation are presented below in Table 2.
| Independent variables |
Regression coefficient |
Standard error (t-statistic) |
|---|---|---|
| Δr(t − 1) | 0.24 | 0.10 (2.34)* |
| Δr(t − 2) | 0.23 | 0.09 (2.48)* |
| Δr(t − 3) | −0.30 | 0.09 (−3.19)** |
| Δr(t − 4) | 0.43 | 0.09 (4.93)** |
| ΔplD (t) | 0.07 | 0.03 (2.20)* |
| Δc(t) | 0.12 | 0.05 (2.70)** |
| Δc(t − 1) | 0.13 | 0.05 (2.72) ** |
| r(t − 1) − c(t − 1) | −0.03 | 0.02 (−2.09) |
| pl(t − 1) − c(t − 1) | 0.02 | 0.01 (1.79) |
| Long-run elasticities | ||
| pl | 0.66 | |
| c | 0.34 | |
| Diagnostics | Test statistic | Significance |
| Ho: First degree homogeneity | F(1,73)=0.04 | |
| Ho: No cointegration | −2.23* | |
| Standard error of equation | 0.01 | |
 |
0.72 | |
| LM(1) serial correlation | χ2 (1)=0.24 | 0.62 |
| LM(4) serial correlation | χ2 (4)=2.54 | 0.64 |
| Notes: (a) The constant term was found to be insignificant and so has been removed. (b) * indicates significance at the 5 per cent level and ** at the 1 per cent level. (c) In the ECM, statistics for differenced terms are distributed standard t; the distribution of the lagged levels is not known. (d) Standard errors and t-statistics for the long-run elasticities could not be generated because of the imposition of first-degree homogeneity. (e) The test of first-degree homogeneity was carried out in the Bewley transformation. |
||
6.1 The Long-Run Relationship
Equation 11 was first estimated as an UECM, with k=5. Insignificant lags were then removed before the corresponding Bewley transformation was estimated. The Bewley transformation provided standard errors which allowed the hypothesis of first degree homogeneity in equation (10) to be tested. This hypothesis was accepted and is imposed in Table 2, so that α + π = 1. The test of cointegration in the RECM suggests cointegration at a significance level of 5 per cent. The long-run elasticities are calculated from the error-correction model; for a 1 per cent increase in the landed import price, the retail price is estimated to increase by 0.66 per cent, while for a 1 per cent increase in domestic costs, the retail price is estimated to increase by 0.34 per cent.
The results suggest that, of the total costs faced by local distributors of imports, 66 per cent is accounted for by the import itself and the remainder by aspects of its distribution and sale.[29] Thus they lend support to the proposition made at the outset of the paper that the effect of an increase in the landed price of an import on its retail price is governed by the share of the imported item in the total costs.[30] In other words, at the second stage, about 66 per cent pass-through may constitute full pass-through.
6.2 Short-Run Dynamics
As previously, if the adjustment to a change in the landed price of an import were instantaneous, retail import prices would follow their long-run equilibrium path exactly. However, the short-run coefficients on price and cost variables reported in Table 2 are both clearly less than their long-run values. Furthermore, response to changes in PL is asymmetric whilst the output gap proves to be insignificant in the short-run dynamics. Consequently, the actual retail price deviates from its long-run equilibrium for lengthy periods, as shown in Figure 4.
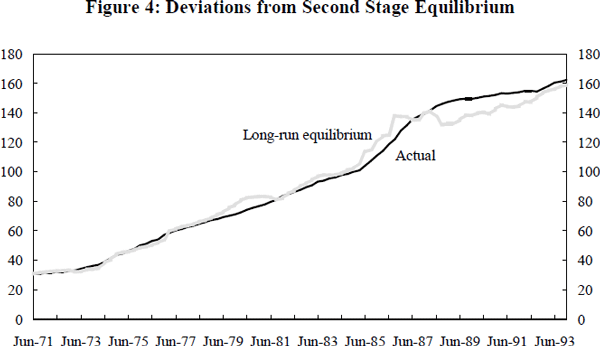
The corollary of such a protracted departure from equilibrium is a gradual adjustment to any shock to the prices of imported or domestic inputs. This implies that the mark-up is also varied for considerable periods of time. Impulse response functions give an insight into the adjustment of retail import prices following a given shock, and permit us to make inferences about the effect of these shocks on the mark-up.
Figure 5 shows the estimated dynamic response of retail import prices to a 1 per cent change in the landed import price during episodes of appreciation and depreciation. Two key results emerge that have important implications for the mark-up. First, the pass-through of changes in the landed import price to changes in the retail price is very slow. It takes about four years before most of the estimated long-run price effect is realised.[31] Such slow pass-through implies considerable variation and persistence in the mark-up.
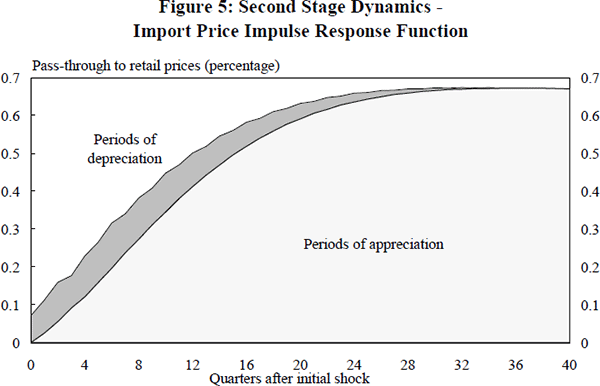
Second, it appears that there is an asymmetry in the speed of response of retail import prices to changes in their landed price. Pass-through of changes in the landed price is slower during appreciations (when such prices fall) than during depreciations (when such prices rise). From this we can infer a corresponding asymmetry in the response of the mark-up to changes in the exchange rate; it increases more quickly during appreciations than it falls during depreciations.
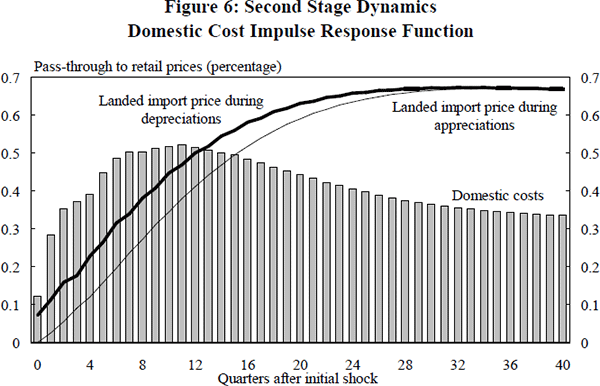
Figure 6 shows the estimated dynamic response of retail import prices to a 1 per cent increase in the cost of domestic inputs. The profile of adjustment is different to that when the landed import price changes. Although a small speed of adjustment parameter ensures that it takes a long time to reach equilibrium, a sizeable proportion of a change in costs is passed on to retail import prices early in the adjustment process. Consequently, variations in the cost of domestic inputs have less influence on the importers' mark-up than changes in the landed import price. This suggests that distributors of imports may perceive changes in domestic costs to be permanent.[32] Changes in over-the-docks import prices, on the other hand, may be seen as transitory, especially given the extent to which they are driven by a volatile exchange rate.
6.3 Combined Pass-Through
The first and second stages of price adjustment, described above, can now be combined to trace the final impact of an exchange rate change on retail import prices. It has been shown that, in the long run, a 1 per cent change in the exchange rate leads to a 1 per cent change in the free-on-board price of an import. In turn, a 1 per cent change in the landed price of an import leads to an 0.66 per cent change in its retail price, in the long run. Thus, assuming that all other costs incurred by the domestic importer are independent of the exchange rate, pass-through of a 1 per cent change in the exchange rate to retail import prices is, in the long run, also about 0.66 per cent. However, to the extent that international freight is an imported service, its price will be affected by the exchange rate, so that combined pass-through is slightly more than this estimate.
This long-run impact is substantial. The short-run impact, however, is not. Although changes in the exchange rate are passed on quickly to over-the-docks prices, these prices are, in turn, passed on only very slowly to those at retail outlets. In addition to such slow pass-through, the adjustment is asymmetric, with the pass-through of landed import prices during appreciations being slower than during depreciations. In fact, as implied by Figure 5, the influence of the exchange rate is so greatly dissipated by the slowness of price adjustment at the second stage that it takes, in the event of depreciation, two years before half of the estimated passthrough is realised. Pass-through is even slower in the event of appreciation. Clearly, the inflationary consequences of exchange rate fluctuations hinge on price adjustment at the second stage, in particular the way in which local distributors elect to vary their mark-ups in response to a given shock.
The nature of price adjustment at the second stage has permitted a number of inferences about the behaviour of the mark-up in response to given shocks. We observe that changes in the costs of imported or domestic imports are not immediately passed on to retail import prices and so infer that the mark-up has changed. The error-correction mechanism, therefore, contains information with which a measure of the importers' mark-up can be constructed. In the next section, such a measure will be presented.
Footnotes
The tariff is not included in the index of domestic costs because ad valorem tariffs represent a loading on the free-on-board price. If all tariffs are ad valorem, then the elasticity of the exchange rate with respect to P should be equal to that with respect to a price with a tariff loading. Hence equation (9) is equivalent to R = δ(PLT)α Cπ. [27]
There is, however, considerable debate in the literature as to the relationship between markups and the business cycle. Whilst Benabou (1992) argues that the relationship is procyclical, Stiglitz (1984) and Layard, Nickell and Jackman (1991) argue that it is counter-cyclical; they claim that, in the presence of imperfect competition, firms have a greater incentive to attract customers during episodes of strong demand (so that the mark-up falls), and to collude in pricing behaviour during recession (so that the mark-up increases). The empirical evidence is mixed (Layard et al. 1991, p. 340). [28]
Predicated on the constant term in the estimating equation capturing a stationary mark-up in the long run. [29]
This estimate of the cost share is roughly consistent with the results published by the PSA (1989). For more details see Appendix 1(f). However, interpretation of these coefficients as costs shares has limitations. An implication of the chosen functional form is that, with constant costs shares, a given increase in R is the result of a corresponding increase in both PL and C. We might not expect that because the price of an imported input has increased that the price of a domestic input will also increase, at least in the short run. Nonetheless, estimates of parameter stability suggest that the coefficients do, in fact, satisfy first degree homogeneity and remain stable over time. [30]
In fact, this result is striking in its similarity to that found by de Brouwer et al. (1994) with respect to the speed of pass-through of aggregate import prices to a measure of the general price level. [31]
Certainly, it is plausible for them to think that an increase in unit labour costs is permanent, given the infrequency with which such costs fall. Unit labour costs comprise the largest share of the cost of domestic inputs. [32]