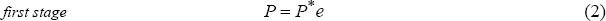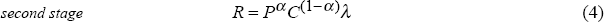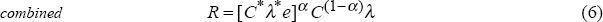RDP 9407: Explaining Import Price Inflation: A Recent History of Second Stage Pass-through 3. Analytical Framework

In essence, exchange rate pass-through is an application of the law of one price.^[7] In its absolute form, the law states that the price of a traded good (for our purposes an import) will be the same in both the domestic and foreign economies, when expressed in a common currency.^[8] The law can be written as follows:

where p is the domestic price of the import, p* is its corresponding world price, and e is the exchange rate (in units of domestic currency per unit of foreign currency). Departures from the law occur when, for a given world price of an import, proportional changes in its domestic price are not identical to those in the exchange rate.

A pass-through relationship can now be expressed in terms of the law of one price. However, the purpose of this paper is to distinguish between first and second stage pass-through. The law will be adapted in two main respects. Import prices will be chosen that are appropriate for the stage of price adjustment. A mark-up model will also be invoked so that a given price comprises a domestic cost component, C, and a mark-up, λ.^[9]

Consider first stage pass-through. It is defined as the elasticity of the domestic over-the-docks import price with respect to the exchange rate. Consequently, the domestic price is now defined as a free-on-board import price, P. We commence with the simple expression:

First stage pass-through is complete when a change in the exchange rate is not associated with a change in the world price so that:

Thus, in the limit, all of a change in the exchange rate can be passed on to a change in the import price over the docks. For a small open economy that is a price taker in world markets, pass-through is expected to be complete.^[10] However, if the economy is not a price taker, foreigners may adjust the foreign currency price of the import following an exchange rate change. Consequently, if one allows for the foreign import price to embody a mark-up (so that P^* = C^*λ^*), it is apparent that, at given costs, foreign suppliers can elect to offset the effects of depreciation on P by lowering their mark-up so that pass-through is incomplete.^[11]

Second stage pass-through is defined as the elasticity of a retail import price with respect to an over-the-docks import price. Now let the domestic import price be defined as a final retail price, R. Employing a simple mark-up model, this price will be determined by the total costs faced by the distributor and a mark-up, where total costs comprise the cost of the import itself and the cost of domestic inputs used in the process of distributing and selling the import. Thus second stage pass-through can be expressed as:

where α represents the share of the import in total costs.^[12]

Although, the full increase in P (and indeed C) will be passed on to R, the proportional change will be less than unity because the imported good is only one element in the bundle of costs faced by the retailer.^[13] Thus second stage pass-through is complete when changes in P do not lead to changes in the importers' mark-up so that:

In other words, complete pass-through is defined by the share of the imported item in the total cost faced by the retailer. Again, however, retailers of an import can, at given costs, elect to offset the effects of an increase in P by lowering their mark-up so that second stage pass-through is incomplete.

These first and second stages can now be combined to trace the full impact of an exchange rate change on the retail price of an import:

As shown in equation (6), the effect of an exchange rate change on the final retail price of an import can be diffused through three main channels: the size of α; variations in the mark-up by foreign suppliers; and variations in the mark-up of local distributors. While understanding the circumstances under which mark-ups are altered requires recourse to dynamic models of imperfect competition, ultimately, the extent and speed of exchange rate pass-through is an empirical question. In this respect, Krugman (1986) argues that what is needed is not more theory but more data to identify these relationships empirically.

The above equations form the basis of a simple model for testing first and second stage pass-through. However, before discussing the functional form and estimation technique to be employed, some of the data challenges involved in measuring pass-through are discussed.

Footnotes

Menon (1991a) provides a detailed discussion of the relationship between the law of one price and exchange rate pass-through. [7]

In its relative form the law allows for a wedge factor of transactions cost. If, however, these costs are constant, both the relative and absolute forms of the law will be equivalent when expressed in log linear form or in proportional changes. [8]

See, for example, Mann (1986) and Hooper and Mann (1989). [9]

Specifically, import price pass-through will approach unity the lower is the price elasticity of demand for imports or the higher is the price elasticity of supply (Spitäller 1980; Bureau of Industry Economics 1987). For a small open economy that faces perfect elasticity of supply, foreigners will not adjust the foreign currency price of the import following a change in the exchange rate so that pass-through will be complete. [10]

Incomplete pass-through introduces issues in pricing to market when the exchange rate changes. For a survey of a series of models (dynamic and static) that seek to explain the microeconomics of pricing to market, see Krugman (1986). [11]

This formulation assumes a standard Cobb-Douglas production function which allows for a unitary elasticity of substitution between the import and domestic inputs. It might be argued that it is inappropriate to assume that the import and domestic inputs are substitutable. For example, the retailer of an imported television is not able to substitute additional labour for one less television and sell the same output. Leontief production technology in which inputs are employed in fixed proportions (regardless of their price) may be more appropriate. Other more flexible production functions could be considered (such as a constant elasticity of substitution or a translog production function). However, such functions are less tractable econometrically and their long-run properties are less transparent. Consequently, we adopted the Cobb-Douglas formulation but recognise the limitations of assuming a unitary substitution elasticity. [12]

However, the pass-through of a proportional change in total costs will be unity (since the cost shares sum to unity). [13]