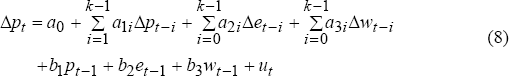RDP 9407: Explaining Import Price Inflation: A Recent History of Second Stage Pass-through 5. Estimating the First Stage of Price Adjustment
December 1994
- Download the Paper 106KB
Recent investigations of exchange rate pass-through have employed an econometric method that combines the concepts of cointegration and error correction.[18] Given that the data to be used in estimation are non-stationary, cointegration techniques will also be employed here.[19]
In brief, if two series are non-stationary, but a linear combination of them is a stationary process, they are said to be cointegrated (Engle and Granger 1987). Importantly, cointegration provides a framework with which to model the long-run equilibrium of an economic system. Furthermore, the presence of a cointegrating relationship implies the existence of an error-correction equation that can describe the short-run dynamics of adjustment towards equilibrium. This is especially pertinent to the examination of pass-through where we wish to identify the long-run relationship (about which economic theory provides strong priors) and the dynamics of adjustment (about which theory can provide little advice).
In this paper, an unrestricted error-correction model (UECM) is used. This one-step procedure is simple and transparent. The efficiency of the estimates of the long-run relationship between variables is enhanced because these estimates are derived whilst taking account of the short-run dynamics.
To estimate first stage pass-through from the exchange rate to free-on-board import prices, we commence with a levels equivalent of equation (2) that allows for a constant so that:[20]
and represents the long-run relationship. It can be re-expressed as a general linear kth-order autoregressive distributed lag (ADL) model and reparamaterised to form an UECM. This permits isolation of information about the long-run relationship between the variables as well as their behaviour in the short run.
The general form of the UECM is:
Variables expressed in lower case are logarithms. This model is initially estimated with k=5. Insignificant variables were eliminated, yielding the parsimonious error-correction model presented in Table 1.
| Independent variables |
Regression coefficient |
Standard error (t-statistic) |
|---|---|---|
| constant | −0.60 | 0.25 (−2.39)* |
| Δe(t) | 0.64 | 0.04 (16.14)** |
| Δe(t − 1) | 0.20 | 0.04 (4.86)** |
| Δe(t − 2) | −0.22 | 0.07 (−3.04)** |
| Δw(t − 1) | 0.59 | 0.12 (5.06)** |
| Δp(t − 2) | 0.23 | 0.09 (2.64)* |
| p(t − 1) | −0.13 | 0.05 (−2.50) |
| e(t − 1) | 0.14 | 0.05 (2.55) |
| w(t − 1) | 0.13 | 0.06 (2.30) |
| Long-run elasticities | ||
| e | 1.01 | 0.067 (14.97)** |
| w | 0.96 | 0.069 (13.84)** |
| Diagnostics | Test statistic | Significance |
| Ho: No cointegration | −2.49* | |
| Ho: β =1 | 0.08 | |
| Ho: θ =1 | 0.62 | |
| Standard error of equation | 0.01 | |
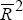 |
0.83 | |
| LM(1) serial correlation | χ2 (1)=1.79 | 0.18 |
| LM(4) serial correlation | χ2 (4)=5.38 | 0.25 |
| Notes:(a) * indicates significance at the 5 per cent level and ** at the
1 per cent level. (b) In the ECM, t-statistics for differenced terms are distributed standard t; the distribution of the coefficient on p(t − 1) lies somewhere between the Dickey-Fuller and N(0, 1) distributions; the distributions of the other lagged levels are not known. (c) The test for cointegration is the significance of the error-correction term in a restricted error-correction model; this is also distributed between the Dickey-Fuller and N(0,1) distributions. (d) t-statistics and hypothesis tests on the long-run elasticities are carried out using standard errors generated from the corresponding Bewley (1979) transformation. |
||
5.1 The Long-Run Relationship
The existence of a long-run cointegrating relationship between the variables can now be examined. The significance of the lagged level of the dependent variable (the “speed of adjustment” parameter) has been proposed by Kremers, Ericsson and Dolado (1992) as a test of cointegration; the result for this test suggests that there is cointegration, although the precise distribution of the test statistic is not known.[21]Another test of cointegration involves testing the significance of the error-correction term, in a restricted error-correction model (RECM).[22] This test is also reported and confirms the existence of cointegration.[23]
The nature of this relationship can be described by the long-run elasticities. In Table 1, long-run elasticities are calculated as the ratio of the lagged level of the explanatory variables to the speed of adjustment parameter. This elasticity for the exchange rate is 1.01, which is not statistically different from unity and confirms that, in the long run, first stage pass-through is complete. A similar result is found for the world price. These results satisfy priors about Australia as a price taker in world markets and accord with earlier findings about first stage pass-through to the price of aggregate imports.[24]
In the pass-through literature, it is implicitly assumed that movements in the exchange rate are exogenous. However, cointegration does not indicate causation; it establishes that a long-run relationship exists. It is conceivable that, in the long run, changes in the exchange rate are endogenous as they may stem from changes in domestic prices relative to those abroad. Thus establishment of a cointegrating relationship between the exchange rate and domestic import prices may merely indicate that, in the long run, purchasing power parity (PPP) holds. It is more likely, though, that differentials between general price levels in domestic and foreign economies drive exchange rate movements in the long run, rather than differentials in the prices of a particular class of goods.[25]
5.2 Short-Run Dynamics
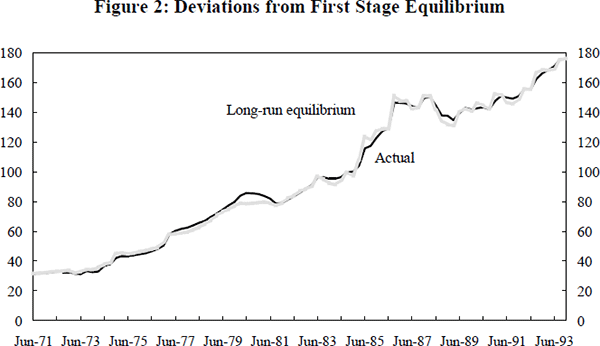
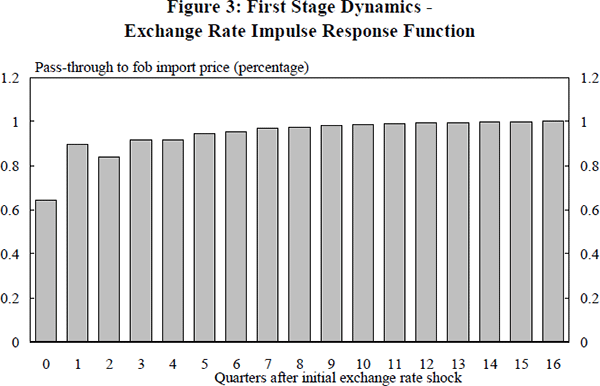
If adjustment to an exchange rate change were instantaneous, import prices would follow their long-run equilibrium path exactly. As shown in Figure 2, actual prices deviate from their long-run equilibrium, although such departures are fairly small, both in their extent and duration. Typically, it appears that there is a return to the equilibrium path within one year. The speed with which prices adjust can be confirmed by the impulse response function derived from the unrestricted error-correction model. Figure 3, shows the estimated dynamic response of import prices to a 1 per cent depreciation. The free-on-board price of consumption imports responds rapidly to changes in the exchange rate. It is estimated to rise by about 0.64 per cent in the quarter in which the depreciation occurs, and by about 0.9 per cent by the fourth quarter. This profile of adjustment is broadly similar to that found for aggregate import prices at the first stage (Dwyer et al. 1993, pp. 14–15).[26]
Footnotes
Menon (1991b) was the first in the Australian pass-through literature to employ cointegration techniques. See also examples by Heath (1991) and, more recently, Dwyer et al. (1993). [18]
Details of the time series properties of the data are reported in Appendix 2. [19]
Given that the law of one price is seldom observed to hold absolutely, by allowing for a constant, ϕ, to represent a “wedge factor” of transactions costs, we can test whether the relative version of the law holds (Officer 1976). [20]
The speed of adjustment parameter indicates how quickly the system returns to equilibrium after a random shock. The distribution of the test statistic for this parameter is not known with certainty, but lies between the Dickey-Fuller distribution in the presence of a drift and the N(0,1) distribution. The observed test statistic falls between these two distributions at the 5 per cent level of significance. [21]
The residuals from the long-run relationship were identified. A restricted error-correction model then specified changes in import prices as a function of these lagged residuals, and changes in the other variables. Because the RECM was found to have an insignificant drift term, the test for cointegration is distributed between the Dickey-Fuller with no drift and N(0,1) distributions. [22]
Kremers et al. (1992) demonstrate that testing the significance of the error-correction term is a more powerful test of cointegration than direct tests based on the residuals of the cointegrating relationship. They also show that the coefficient on the error-correction term is parametrically equivalent to that on the speed of adjustment parameter. [23]
Full pass-through of the exchange rate and world prices to the domestic price of aggregate imports has been found by Phillips (1988) and Dwyer et al. (1993). [24]
Furthermore, the contemporaneous exchange rate and world price are exogenous to changes in the domestic import price, as shown in Appendix 3. [25]
In fact, the speed with which equilibrium is reached is further evidence that in our cointegrating relationship, exchange rate changes cause changes in domestic import prices. We would not expect that, over time horizons of only a few quarters, exchange rate movements are explained by differentials in the domestic and world price of imports; to the extent that PPP is observed to hold, it is observed over much longer time horizons. Rather, we would expect that changes in domestic import prices are being explained by exogenous swings in the exchange rate. [26]