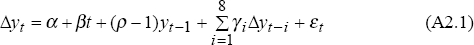RDP 9407: Explaining Import Price Inflation: A Recent History of Second Stage Pass-through Appendix 2: Time Series Properties of the Data
December 1994
- Download the Paper 106KB
Each of the series used in estimating cointegrating relationships was tested for non-stationarity using the Augmented Dickey-Fuller test (Said and Fuller 1984). The null hypothesis of this test is non-stationarity. The following procedure was adopted. Initially equation A2.1 was estimated for each time series yt.
Eight lags of the dependent variable were included to eliminate autocorrelation; the lags were then sequentially removed until the minimum number of lags required to avoid autocorrelation was reached.
The joint hypothesis, β = 0,ρ −1 = 0, was then tested. The results of this test are shown in the first column of table A2.1. Where the hypothesis was rejected, a test was conducted to see whether the series is integrated around a deterministic trend; thus the hypothesis ρ −1 = 0 was tested. These results are shown in the second column below.
|
Null hypothesis: |
(a) Unit root & no trend |
(b) Unit root given trend |
(a) Unit root & no drift |
(b) Unit root given drift |
|---|---|---|---|---|
| Variable | ||||
| First stage pass-through |
||||
| p | 2.579 | ~ | 4.673 | ~ |
| e | 4.640 | ~ | 2.202 | ~ |
| w | 11.763** | −2.392 | ~ | ~ |
| Δp | 8.211* | −3.841* | ~ | ~ |
| Δe | 7.400* | −3.601* | ~ | ~ |
| Δw | 16.219** | −5.455** | ~ | ~ |
| Second stage pass-through |
||||
| r | 6.873* | −2.669 | ~ | ~ |
| pl | 2.380 | ~ | 4.351 | ~ |
| c | 4.098 | ~ | 6.775* | −2.797 |
| Δr | 9.854** | −4.157** | ~ | ~ |
| Δpl | 10.607** | −4.315** | ~ | ~ |
| Δc | 12.422** | −4.689** | ~ | ~ |
| Notes: * indicates significance at the 5 per cent level and ** at the 1
per cent level. (a) Critical values are tabled in Perron (1988). (b) Critical values from Fuller (1976). |
||||
If the initial joint hypothesis was accepted, equation A2.1 was re-estimated with a constant but no trend. The null of a unit root and no drift was then tested (α = 0,ρ −1= 0). If this hypothesis was rejected, we tested whether the rejection was due to a significant drift term, stationarity, or both. This was done by testing for a unit root given a drift. The results, reported in Tables A2.1, suggest that the series are all integrated of order one.