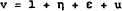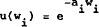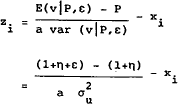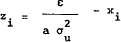RDP 8707: Asymmetric Information and Bid-Ask Spreads in the Eurocurrency Markets 2. The Model

We consider a market for a single risky security in which all trade is transacted through a single professional intermediary (the “dealer”). The dealer is assumed to be risk neutral and competitive, so that he always sets prices at break even point. In addition to the dealer the market is made up of potential customers (“traders”). The dealer transacts with traders one at a time, and the order in which they are selected for trade is, from the dealer's point of view, random (or at least uncorrelated with other information of relevance to the dealer). On the arrival of each trader the dealer announces the prices at which he is willing to buy or sell the security and the trader is then permitted to buy or sell a fixed quantity or not to transact.

The asset pays a random return of v, where

at a fixed date (time T) in the future. Thus ν is the sum of three random components, and we asume that the first two of these are observed privately, before the market opens, by the dealer and the traders respectively. The third component u represents pure uncertainty and is not known until time Τ when the asset return is realised. In the absence of all uncertainty the asset would have unit value. The distributions of the random variables are assumed to be normal, each with zero mean, and variances 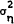, 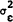and 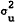respectively; the three components are independent. Asymmetric information thus enters the model in the form of uncertainty about the location of the mean, while variances are common knowledge. This structure ensures that the conditional distributions of ν given a subset of the full information set, remain normal.

The model assumes that traders have exponential utility functions, that is, utility functions of the form

where a_i is trader i's coefficient of absolute risk aversion and w_i is his end of period wealth. With normally distributed asset returns, this implies that the traders have linear asset demand functions of the form

where μ_i, 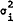are trader i's estimates of the mean and variance of the asset return, x_i is his initial endowment and x_i is the relative price of the asset in terms of a risk-free numeraire.

To reduce the number of unknown parameters in the demand function to just two, I assume that traders have equal coefficients of risk aversion. Endowments vary however, and the endowment of each trader is assumed to be drawn independently from a normal distribution with parameters 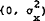. (The possibility of negative holdings is perfectly reasonable in a currency market where a posiive holding represents a deposit and a negative holding an overdraft.) These endowments might be thought of as being determined in the real sector (perhaps, in the context of a foreign exchange market, by real trade).

We now consider the pricing policy of the dealer. To illustrate the necessity of setting a spread between bid and ask prices, suppose the dealer were to set a single price P for buying and selling. Clearly the best he could do in this case would be to set P equal to the expected value of the asset given the information available to him, i.e. P = 1 + η. The first trader to arrive has a demand function

since the trader can infer η from P. This simplifies to

The trader will buy (z_i > 0) if 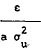> x_i, that is, if

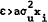. What is the dealer's expected gain on the first transaction if the first trader is a buyer? This is given by

which is negative, since the unconditional expectation of e is zero. Thus the dealer expects to make a loss oh the first transaction if the first trader buys. For similar reasons, he also makes a loss if the first trader sells. He cannot break even with a single buying and selling price because traders will use the information contained in price combined with their own private information to extract a positive expected return.

Suppose instead that the dealer sets separate bid and ask prices (B and A respectively). The zero profit conditions on the two prices can be written as

where b is the information that the next trader chooses to buy and s is the information that he sells. This condition requires that every transaction is fair in expected value terms relative to the dealer's ex-post information (the information as to whether the trader buys or sells). It rules out a strategy of (for instance) making expected losses on purchases matched by gains on sales, while breaking even overall, and ensures that the equilibrium bid and ask prices are symmetric about the dealer's conditional mean.

The following section examines equation (2) to show the nature of equilibrium in this model.