RDP 8707: Asymmetric Information and Bid-Ask Spreads in the Eurocurrency Markets 5. Empirical Implications and Results
October 1987
- Download the Paper 591KB
In this section we focus on how the qualitative predictions of the model might be tested.
The model is highly stylised and contains several unobservable variables, so it is not
possible to subject the model as it stands to rigorous empirical testing. There are however
two implications which can be tested at a more general level. The first is that the spread
is a function of the variance of the asset price; this was established in proposition 2.
Econometrically, this implies that the spread would be a predictor of the squared change in
he actual asset price. Moreover, the direction of this correlation has a straightforward
intuitive interpretation. The relationship between spread and variance is positive for the
asymmetric information component of variance 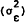 and negative for
the pure uncertainty component
and negative for
the pure uncertainty component 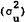 . Thus a positive relationship
between spreads and variances may be taken as evidence that the asymmetric information
component predominates.
. Thus a positive relationship
between spreads and variances may be taken as evidence that the asymmetric information
component predominates.
A second implication is as follows. Suppose the dealer is risk averse.[1] Assuming the dealer holds positive stocks, this would imply that his average price (average of bid and ask) would be at a discount from the risk neutral case; the dealer would require a higher expected return as compensation for risk. The expected excess return will be positively related to the conditional variance, and hence will be positively related to the spread if the asymmetric information component of uncertainty predominates.
In order to test these two qualitative predictions using data on the foreign exchange markets, a simple model of the relationship between forward and spot exchange rates is used. This is taken from Fama (1984). The model is written as
where St is the log of the spot exchange rate at t (in U.S. dollrs), ft,j is the j-period forward premium, and εt+j is an expectational error uncorrelated with information available at t. Under the joint null hypothesis of risk neutrality and market efficiency, α=0 and β=1. An alternative expression is to use
which makes use of the fact that the interest differential must be equal to
the forward premium by covered interest parity. Here rt,j and 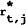 are
the j-period nominal interest rates for foreign and U.S. currency deposits respectively.
Under the null hypothesis β1 =β2 =1.
are
the j-period nominal interest rates for foreign and U.S. currency deposits respectively.
Under the null hypothesis β1 =β2 =1.
Our interest in this paper is not primarily in estimating equations (10) and (11). There is
already a large literature which thoroughly examines such equations (see for example Hansen
and Hodrick (1980,1983) and Fama (1984)). Rather, the purpose is to test whether in the
context of these simple models, variables which measure bid-ask spreads enter significantly
as positive predictors of the mean and variance of St+j. Two sets of tests are
therefore carried out: first, we test whether bid-ask spreads enter as significant
additional regressors in equations (10) and (11); secondly, spreads are tested as predictors
of the squared residuals 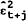 generated by those equations. The
tests are applied to three exchange rates against the U.S. dollar: the Pound Sterling,
Deutschemark, and Swiss Franc, and for contract maturities of one and three months in each
case (i.e. j=1 or 3 in equations (10) and (11)). Monthly data are used for the period 1973:7
to 1984:12. Nominal interest rates are Eurocurrency, deposit rates, which ensures
consistency between forward premia and measured interest differentials. For each equation,
three bid-ask spreads are tested: these are the spreads on the forward exchange rate, and on
the U.S. and the relevant foreign deposit rates, for the appropriate maturities. All data
are obtained from the Financial Times.
generated by those equations. The
tests are applied to three exchange rates against the U.S. dollar: the Pound Sterling,
Deutschemark, and Swiss Franc, and for contract maturities of one and three months in each
case (i.e. j=1 or 3 in equations (10) and (11)). Monthly data are used for the period 1973:7
to 1984:12. Nominal interest rates are Eurocurrency, deposit rates, which ensures
consistency between forward premia and measured interest differentials. For each equation,
three bid-ask spreads are tested: these are the spreads on the forward exchange rate, and on
the U.S. and the relevant foreign deposit rates, for the appropriate maturities. All data
are obtained from the Financial Times.
The regression results appear in Tables 1 and 2. Table 1 shows the estimated coefficients in the variance prediction equations. These results provide no clear support for the theory, with the spread variables being significant predictors of variances in only two of the six equations. Much more striking however are the estimated coefficients in the equations for expected returns. Table 2 shows estimates of equations (10) and (11), augmented by the inclusion of the relevant spread variables as additional regressors. The results show that almost all the equations have significant coefficients on at least one of the spread variables, a fact that is interesting in its own right in view of the generally recognised difficulty in finding significant predictors for exchange rate movements. The forward rate spreads, when they are significant, tend to predict positive future movements in the value of the associated currency against the U.S. dollar. This is consistent with the interpretation that significant asymmetric information effects are present and make a relatively large contribution to the degree of uncertainty in these markets. The other interesting feature is that speads on U.S. dollar deposit rates are negatively correlated in most cases, with future changes in the value of the other currencies against the dollar (and hence positively correlated with future changes in the dollar's value against the other currencies). Thus a large spread on the U.S. dollar deposit rate is associated with a discount from the current value of the dollar, which again is in line with the asymmetric information interpretation.
| Currency & Maturity | U.S. interest rate spread | Foreign interest rate spread | Forward premium spread | U.S. interest rate | Foreign interest rate |
|---|---|---|---|---|---|
| £ (1) | −0.07 (1.76) |
−0.0003 (0.11) |
0.04 (0.54) |
−0.11 (2.50) |
0.05 (1.27) |
| £ (3) | −0.22 (1.35) |
−0.23 (2.25) |
0.03 (0.07) |
−0.08 (1.36) |
−0.18 (3.22) |
| DM (1) | 0.02 (0.39) |
−0.03 (0.39) |
−0.04 (0.31) |
−0.207 (2.74) |
0.02 (0.25) |
| DM (3) | −0.08 (0.49) |
−0.11 (0.86) |
−0.21 (0.56) |
−0.09 (1.07) |
−0.04 (0.36) |
| SF (1) | 0.02 (0.35) |
−0.04 (0.63) |
0.30 (2.96) |
−0.12 (1.17) |
−0.06 (0.55) |
| SF (3) | 0.10 (0.42) |
−0.09 (0.38) |
0.28 (0.78) |
−0.19 (1.38) |
0.08 (0.54) |
|
Notes: (a) Figures in parentheses in this table are t-statistics. |
|||||
| Currency | Maturity (months) | Constant | Forward Premium | U.S. Interest Rate | Own Interest Rate | Spread on U.S.Interest Rate x 10−4 |
Spread on Own Interest Rate x 10−4 |
Spread on Premium x 10−2 |
|---|---|---|---|---|---|---|---|---|
| U.K. £ | 1 | −0.015 (0.011) |
−1.24 (0.83) |
1.71 (0.89) |
−4.76 (2.09) |
1.84 (1.07) |
12.25 (9.82) |
|
| 3 | −0.037 (0.025) |
−1.45 (0.68) |
1.76 (0.72) |
−16,68 (4.53) |
4.36 (3.87) |
40.51 (24.91) |
||
| U.K. £ | 1 | −0.012 (0.009) |
−1.56 (0.71) |
−4.76 (2.08) |
1.62 (1.01) |
13.77 (9.14) |
||
| 3 | −0.026 (0.21) |
−1.75 (0.61) |
−16.38 (4.49) |
3.18 (3.45) |
47.70 (23.12) |
|||
| D-Mark | 1 | −0.009 (0.016) |
−1.49 (1.49) |
1.31 (1.84) |
−3.77 (3.11) |
−1.04 (3.90) |
1.36 (0.73) |
|
| 3 | −0.035 (0.030) |
−1.09 (0.94) |
0.94 (1.22) |
−14.57 (5.35) |
−11.98 (7.35) |
6.32 (1.27) |
||
| D-mark | 1 | −0.013 (0.013) |
−1.12 (1.40) |
−3.64 (3.03) |
−1.07 (3.88) |
1.41 (0.66) |
||
| 3 | −0.038 (0.025) |
−1.13 (0.94) |
15.25 (5.50) |
−12.95 (9.55) |
6.71 (1.4) |
|||
| S-Franc | 1 | −0.008 (0.018) |
−2.91 (1.33) |
3.38 (1.54) |
1.41 (3.92) |
−11.54 (7.39) |
2.39 (0.59) |
|
| 3 | −0.034 (0.036) |
−2.19 (0.87) |
2.16 (1.01) |
−16.60 (6.91) |
−1.70 (9.43) |
4.95 (1.33) |
||
| S-Franc | 1 | 0.007 (0.017) |
−2.66 (1.19) |
1.64 (3.88) |
−10.70 (7.15) |
0.38 (0.59) |
||
| 3 | −0.041 (0.034) |
−1.96 (0.84) |
−17.00 (6.93) |
−1.21 (9.36) |
4.85 (1.33) |
|||
|
Note: (a) Figures in parentheses are standard errors. |
||||||||
It will be noted that the estimates of the coefficients β, β1 and β2 are in general significantly different from their values under the null hypothesis. Similar results for the spot-forward parity equations are reported by Fama (1984). Re-estimation with the spread variables excluded shows that the estimated coefficients are not very sensitive to this change of specification. Thus although the informational effects captured by the spread variables are statistically significant, they make no substantial contribution to explaining the violations of the parity conditions that have been -documented in earlier studies.
Footnote
No attempt is made here to formalise the equilibrium for the risk averse case. This would require a separate and much more complicated analysis. Here only an informal argument is presented to provide motivation for the second set of empirical tests that are reported. [1]

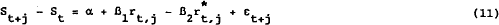
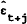 is the OLS residual from the equation referred
to in the first column.
is the OLS residual from the equation referred
to in the first column.