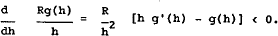RDP 8707: Asymmetric Information and Bid-Ask Spreads in the Eurocurrency Markets 3. Equilibrium
October 1987
- Download the Paper 591KB
It is necessary here to deal only with the ask price A, since the bid price is determined by an exactly similar argument. We can simplify expression (2) as follows.
Here b represents the fact that
Thus we can rewrite (3) as
This defines the break-even point for the ask price. It is not immediately obvious that
there exists a k which satisfies (4). In order to show this we need to examine the
properties of the function defined in this expression. First we define 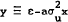 , and
note that e and y have a bivariate normal distribution. We can use the formula for
conditional expectation of a bivariate normal (Mood, Graybill and Boes (1974), p.167)) to
write
, and
note that e and y have a bivariate normal distribution. We can use the formula for
conditional expectation of a bivariate normal (Mood, Graybill and Boes (1974), p.167)) to
write
where we define R to be the ratio of the variance of the traders' signal 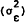 to the
variance of the traders' criterion function
to the
variance of the traders' criterion function 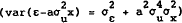 .
.
We can now simplify expression (4) as follows:
where f(t) is the conditional density function for t(= ε − 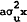 ) given
that t ≥ k. Equation (6) can be written as
) given
that t ≥ k. Equation (6) can be written as
The unconditional distribution of t is normal with parameters (0, σ2),
where σ2 = 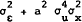 .
.
Next we standardise (7) by noting that
where h = k/σ and r has a standard normal distribution. Finally, using (7) and (8) we can rewrite the basic equilibrium condition that was given by equation (4).
where h satisfies h = RE(r|r ≥. h)
Equation (9) defines the break-even ask price for the dealer. By exactly similar reasoning it can be shown also that
so that bid and ask prices are set symmetrically about the dealer's conditional mean.
It still remains to find the function g(h). For reasons described in the appendix, an analytical expression for this function cannot be obtained, and hence we cannot solve explicitly for the equilibrium value of h. We can however obtain the following properties of the function which will be useful in describing the nature of equilibrium. Moreover the values of the function can be accurately tabulated using the standard normal distribution tables. Here we note three properties of g(h) for h>0. These are proved in the appendix.
- g(h) is continuous.
- The function is bounded by h < g(h) < h + 1/h
- The slope is bounded by 0 < g'(h) < 1.
Figure 1 below illustrates the nature of equilibrium
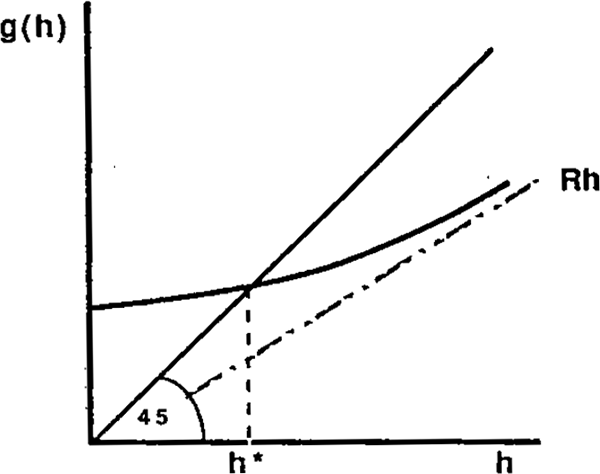
Intuitively Rg(h) represents what the dealer estimates to be the expected value of the trader's information advantage, for a given h. This increases with h (the standardised spread size) because the higher is h, the higher ε must be (other things being equal) to induce a trader to buy; however it increases more slowly than h because the dealer will rationally attribute some proportion of the demand at any price as arising from a liquidity motive. Equilibrium is at the break even point h*, where the expected value of the traders' informational advantage is just equal to the premium charged by the dealer.
The diagram suggests that a unique equilibrium exists. This is formalised by the following proposition.
Proposition 1: There exists a unique break-even point h* if and only if 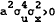 .
.
| Proof: |
(i) Existence follows directly from properties 1 and 2. It is readily seen
that g(0)>0. Also, from property 2, if R<1 there exists an h such that
Rg(h) is arbitrarily close to Rh(<h) and, by continuity, there exists an
h* such that Rg(h*)=h*. If R=l (which is true if and only if (ii) Uniqueness is proved by noting that Rg(h)/h is a strictly decreasing function of h: |
Therefore the equation Rg(h)/h = 1 can have at most one solution.
The condition that 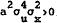 , simply requires that there be some
variation in endowments and some underlying uncertainty that matters, so as to ensure the
presence of a non-zero expected volume of liquidity trading. In other words, for any price
there must be a non-zero probability that the next trader will take an expected loss in
order to cover an initial risky position. Provided this is so, raising the ask price of the
asset will cause its expected value (conditional on the dealer's ex-post information) to
increase less quickly, because the dealer will be unsure whether to interpret the trader's
willingness to buy as an indication of a favourable value signal (high ε) or of a
low endowment (low x).
, simply requires that there be some
variation in endowments and some underlying uncertainty that matters, so as to ensure the
presence of a non-zero expected volume of liquidity trading. In other words, for any price
there must be a non-zero probability that the next trader will take an expected loss in
order to cover an initial risky position. Provided this is so, raising the ask price of the
asset will cause its expected value (conditional on the dealer's ex-post information) to
increase less quickly, because the dealer will be unsure whether to interpret the trader's
willingness to buy as an indication of a favourable value signal (high ε) or of a
low endowment (low x).
It is clear from the equilibrium condition (9) that the size of the spread is a function of
the parameters which determine R, that is, the variance terms 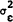 ,
,
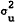 and
and
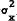 , and
the coefficient of risk aversion.
, and
the coefficient of risk aversion.
Obviously an increase in the ratio R increases the standardised spread h, but the influence of each parameter on the total spread k(=hσ) is not immediately obvious. The directions of these effects are given in the following proposition (which is proved in the appendix).
Proposition 2: The equilibrium spread k* is an increasing function of the variance of
the traders' signal 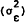 and a decreasing function of
and a decreasing function of
-
the variance of endowments
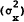
-
the variance of the noise component (
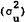 )
)
- the coefficient of risk aversion (a).
This can be summed up by saying that the spread decreases with those factors which tend to
increase the relative importance of liquidity trading as against speculative trading. A high
coefficient of risk aversion for example indicates a willingness of traders to accept
relatively unfavourable trades in expected value terms in order to reduce the risk to which
they are exposed by their initial allocation. The spread required to break even against such
traders would be smaller than for those who were less risk averse. In the limit, if traders
are risk neutral, no spread would be large enough to allow the dealer to break even since
the traders' criterion functions would ensure that they only ever transacted at an
expected profit to themselves. Perhaps slightly counterintuitively, an increase in pure
uncertainty 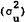 has a similar effect in reducing the spread since
it tends to discourage informational trading by risk-averse traders.
has a similar effect in reducing the spread since
it tends to discourage informational trading by risk-averse traders.
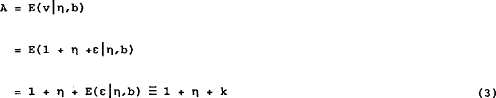
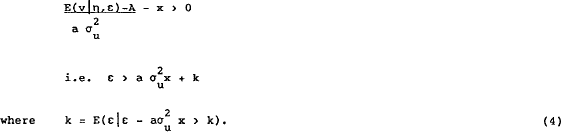
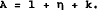
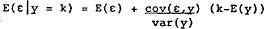




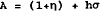

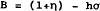
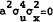 ) then Rg(h)>h for all positive h, so no
equilibrium exists.
) then Rg(h)>h for all positive h, so no
equilibrium exists.