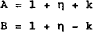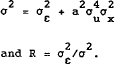RDP 8707: Asymmetric Information and Bid-Ask Spreads in the Eurocurrency Markets 4. A Numerical Example
October 1987
- Download the Paper 591KB
To give an idea of the orders of magnitude involved consider the following simple numerical example. Recall that the equilibrium prices are given by
| where | k = hσ |
| h satisfies h = RE(t|t ≥ h) | |
| the unconditional distribution of t is a standard normal |
The variances 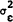 and
and 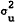 are, roughly
speaking, variances in proportionate rates of return, since the unconditional expected value
of the asset is standardised to one. Thus k is interpreted as the spread size for an asset
of unit value. A reasonable representative value of the coefficient of risk aversion may be
obtained roughly as follows. For any individual, ai
= γi/wi where γi is his coefficient of relative
risk aversion, wi is his wealth. Supposing γi=2, and
wi=$100,000, this gives us a value of a=2×l0−5. Assume also
that σε =.01 and σu =.02, and σx
(the representative desired transaction size) equal to $5m, which seems a reasonable value
for a wholesale market. From this we can calculate that σ=.04, R=.06.
are, roughly
speaking, variances in proportionate rates of return, since the unconditional expected value
of the asset is standardised to one. Thus k is interpreted as the spread size for an asset
of unit value. A reasonable representative value of the coefficient of risk aversion may be
obtained roughly as follows. For any individual, ai
= γi/wi where γi is his coefficient of relative
risk aversion, wi is his wealth. Supposing γi=2, and
wi=$100,000, this gives us a value of a=2×l0−5. Assume also
that σε =.01 and σu =.02, and σx
(the representative desired transaction size) equal to $5m, which seems a reasonable value
for a wholesale market. From this we can calculate that σ=.04, R=.06.
The value of h is calculated using h=Rg(h). This can be solved numerically to give h=.05 when R=.06. Thus we obtain for this example that k=hσ=.002, i.e. a spread of about 0.2 per cent of value. This is quite close to standard spreads in the foreign exchange market. Of course this constitutes no evidence for the model, but simply illustrates that it yields plausible orders of magnitude. It also illustrates the point that quite small, even apparently negligible, spreads can be indicative of a much larger degree of uncertainty or of difference of beliefs (as measured by σu and οε respectively). In this case the standard error of prices due to these two sources is about ten times the order of magnitude of the spread.