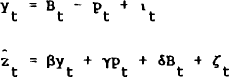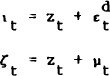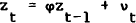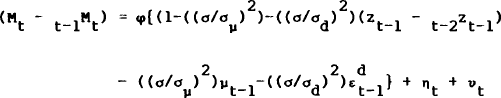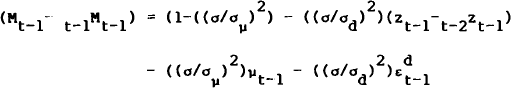RDP 8601: New Classical Models and Unobserved Aggregates 6. Comparison with Other Models

It was shown above that the assumption that agents could not observe any values of the true money supply produced persistence of demand shocks in the solution for the deviation of real output around its natural rate. This source of persistence is different from most other explanations found in the literature which rely on the adjustment of capital (Lucas (1975)) or labor (Sargent (1978)) to shocks (leading to persistence in the natural rate of output); or the adjustment of inventories (Blinder and Fischer (1981)) or staggered wage contracts (Taylor (1980)) to shocks (leading to persistence in the deviation of output around its natural rate). It does, however, have some similarities with the explanation put forward by Brunner, Cukierman and Meltzer (1980). (Hereafter referred to as “BCM”).

In BCM's model, persistence in prices and unemployment is explained by postulating a particular structure for the stochastic demand and supply shocks that perturb the economy. It is assumed that each of these disturbance terms consists of a permanent (random walk) and a transitory (white noise) component. Agents have complete knowledge of the past values of all variables and of the total shocks. They cannot, however, distinguish between the permanent and transitory components of these shocks. Under rational expectations, the solution to this filtering problem induces a persistent response of unemployment and prices. This property of their model rests on the demonstration by Muth (1960) that adaptive expectations are rational when the variable concerned is the sum of a random walk and white noise, with the individual components unobserved. BCM have subsequently used these results in Brunner, Cukierman and Meltzer (1983).

The current model can be shown to have some similarities to this basic mechanism of BCM's model. Observe that the equations of this model can be partitioned into two (simultaneous) blocks; one that contains only observable variables and disturbance terms (equations (1), (3), (5), and (6))), and one that also contains unobservable variables and disturbance terms (equations (2), (4), (7), and (8)). Rewriting equations (2) and (8) after substitution with the identity (4), yields

where ι_t and ζ_t are defined by

Let χ = ψ = ω = 0 and equation (7) becomes

This block of the model may now be seen to have a BCM (or at least a Muth (1960)) mechanism at work as φ → 1.^[20] Since agents know the lagged values of Y_t, P_t, 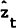and B_t, they can deduce the lagged values of ι_t and ζ_t. These “shocks” to demand and the measured multiplier consist of an unobservable, permanent (random walk) component, z_t, and unobservable, transitory (white noise) components, 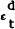and µ_t.

Although the algebra of these two models are similar, their economic motivations are very different. The BCM result obtains in a general model with very specific assumptions about the intertemporal structure of the stochastic disturbance terms. The results in this essay do not depend on assumptions about the structure of the stochastic shocks that perturb the economy. They depend only on the existence of an unobserved (or imperfectly measured) aggregate variable, whose true values are partly determined by at least one of its own lagged values. It is a central tenet of this paper that this relaxation of the usual New Classical assumptions is one that is likely to be encounted in practice.

The recent paper of Boschen and Grossman (1982) (hereafter referred to as BG) also bears some relevance to the current analysis. Their paper presents a New Classical model in which the information set is assumed to include published official preliminary estimates of the contemporaneous money supply. These preliminary estimates are subsequently revised by the authorities as the true values become available. On the basis of some empirical observations, BG assume that the measurement error in the current estimate of the contemporaneous money stock is positively correlated with today's measurement error in last period's money stock. They also assume that each of these errors is serially independent and uncorrelated with the other disturbance terms in the model.

In their model BG assume that the authority's published estimates are always the rational expectations of the appropriate money stocks, given the relevant information sets. Using this, they show that the correlation In the revisions of these official estimates induces persistence into the output equation. Unfortunately, Mankiw, Runkle and Shapiro (1984) have shown, using BG's data, that these revisions are partly forecastable. Hence, the published estimates can not be rational expectations.

The current model, on the other hand, does not assume that the measured money stock is the optimal predictor of the true one, nor is there any contemporaneous information available to agents. Moreover, the analysis is concerned with measurement errors that involve a (permanent) conceptual component rather than just a (temporary) statistical one. These points aside, there is a similarity in the mechanisms generating persistence of demand shocks in the solutions for output. However, in the BG case this mechanism is implicit in the assumption of positive covariance mentioned above, while in the current model such covariances are determined by the solution. To formalise a comparison, the current model may be re-interpreted in the BG paradigm. That is, assume that the authorities publish _t−1M_t and _t−1M_t−1 during period t as their preliminary estimate of the contemporaneous money stock and their revised estimate of last period's money stock, respectively.^[21] Now consider the solution for the error in today's estimate of the contemporaneous money stock,

Application of equation (19) gives the error in today's estimate of last period's money stock as

Provided φ > 0, these two errors will be positively correlated (the unconditional covariance is φσ²) as BG assume in their model. To this extent, these results endogenise BG's assumptions. However, the same two equations also predict that these errors will be correlated with (lagged values of) the demand shocks and will not be serially independent. This suggests that BG's assumptions are mutually inconsistent.

The “persistence” of demand shocks in the solution for output in the current model and the BG model, and in the solution for unemployment in the BCM model, is of a special character. In each case, the relevant variable contains a moving average of demand disturbances and yet is serially uncorrelated in the usual unconditional sense.^[22] To illustrate this property, consider the case of the current model.

Recall from equation (23) that the solution for the error in the agents' expectation of the money stock is an infinite moving average of demand disturbances. As mentioned before, these errors are serially correlated in the usual sense^[23] – indeed they are generated by a first order autoregressive process. From equation (10), output is just the sum of this expectational error and two white noise disturbance terms. However, even though output is a function of this same infinite moving average term (equation (24)), the (unconditional) covariance of output and lagged output (and hence, the serial correlation coefficient) is zero. Mathematically, this is because the weights of the moving average are terms in σ², which solves a particular quadratic equation given in the Appendix.^[24] Intuitively, since output is an observed variable its unanticipated values must be serially independent (in the unconditional sense) by the orthogonality principle. Given the Lucas supply specification (of equation (1)), output must also be serially independent in the usual sense.^[25]

Nevertheless, demand shocks do persist in the solution for output.^[26] Consider an experiment where drawings are made from the distributions of the stochastic shocks so that a “sample” < Y_i, P_i, B_i, 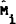> from t_o to T is is generated. Now generate a second sample using the same sequence of drawings for the stochastic shocks as before, except that for some i=t^* (between t_o and and T) replace either ν_i, μ_i or 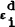by a new drawing from the relevant population. A comparison of the resulting sequences for output in these two samples will show that the effects of a demand shock (i.e. a different drawing) will persist for many periods beyond t^*.

BCM note that their model has this property and suggest that the relevant serial correlation coefficient is one that is conditional on the value of some past shock. In the current model, conditional covariances such as cov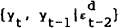 are non-zero.^[27] Perhaps a more relevant measure is the serial correlation of the deviations of output around its complete information level (the level that would pertain with a zero measurement error). In the current model these deviations have a first order serial correlation coefficient of φ²[1−((σ/σ_μ)²)−((σ/σ_d)²)]².

Footnotes

When φ = 1, this version of the model is no longer covariance stationary and the previous results cannot be applied. The solution could be calculated by modifying the method outlined in Muth (1960) to utilise the information on z_t contained in both ι_t and ζ_t. [20]

Note that in my notation the information set available during period t is I_t−1, not I_t as in BG's notation. The re-interpretation of the model allows BG's perceived/unperceived money distinction to be addressed. It is not, however, a very good interpretation because it implies an inconsistent monetary authority – why publish both 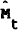and _tM_t at the end of period t, when _tM_t is the optimal measure? [21]

This abstracts from the exogenous source of persistence (a(L)) in the BG model and from the supply shocks in the BCM model. [22]

It may be shown that cov{(M_t − _t−1M_t),(M_t−1 − _t−2M_t−1)} = φσ². A similar result holds for the unobservable permanent shocks in the BCM model. [23]

In the BCM model λ has this property. [24]

Since output and unanticipated output are equivalent. This result also holds for output in the BG model (abstracting from the exogenous a(L) term) and for unemployment in the BCM model. [25]

Current demand shocks “Granger-cause” future output. This is analogous to the bivariate transfer function model in time series analysis (where the leads and lags between the white noise residuals of two ARIMA models are modelled). See, for example, Granger and Newbold (1977). Sargent (1979, p. 256) points out that serial correlation and business cycle persistence are not analagous. Indeed, output displays very little serial correlation of an order that could be associated with business cycles. This distinction clearly deserves more attention in the literature. [26]

Note, however, that in their paper BCM neglect to subtract the conditional means when doing the covariance calculation. The correct conditional covariance will not depend on the value of the conditioning shock. Their discussion about the size of this shock relative to its variance is, therefore, incorrect. See Brunner, Cukierman and Meltzer (1980, section 5.2). [27]