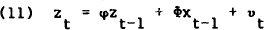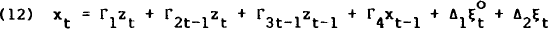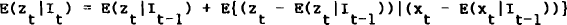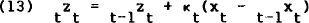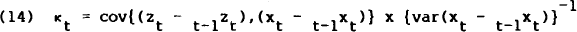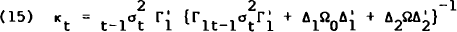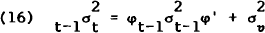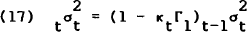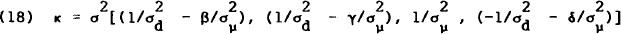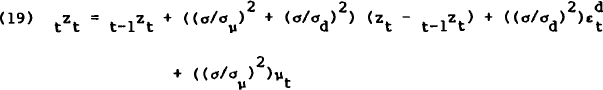RDP 8601: New Classical Models and Unobserved Aggregates 3. An Application of the Kalman Filter

At the end of period t, agents can update their information sets by observations on current output, prices, the measured money supply and the monetary base. (This information can also be used at the beginning of the next period to generate expectations for period t+1.) Agents cannot observe the true money supply (or the true money multiplier), but they can use this new information to update the expectations that they held at the beginning of the period, generating end of period estimates of the unobservable variables. The Kalman filter provides such an updating process. In this model it corresponds to the rational expectations solution. It is more easily derived by moving to a more compact notation.

Rewriting equation (7) in terms of the vector of information that becomes available at the end of period t, x_t, gives

where Φ = [χ, ψ, O, ω] and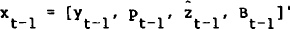

After substituting out the identities (4) and (5), equations (10), (9), (8) and (6) may be stacked,

where the coefficient matrices are given in the Appendix 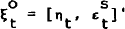and and .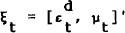

In this compact notation, it is assumed that 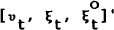is independently and identically distributed N(O,Σ) where 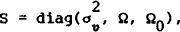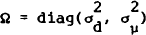and 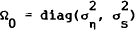. The sequence 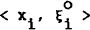is assumed to be contained in I_t−1, but no elements of the sequence < z_i, ν_i, ξ_i > are contained in I_t−1. Given these assumptions, it may be shown that

where χ_t is the vector of information that becomes available at the end of period t. This “recursive projection” formula (Sargent (1979, p.208)) reduces to

where κ_t is the vector of Kalman filter coefficients given by^[10]

The recursive set of equations for κ_t are

where 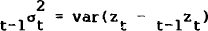and 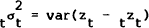. These results are derived in the Appendix.

Equations (13), (15), (16) and (17) define the resursive set of equations that optimally solve the agents' projection problem. If the model is covariance stationary, then this filter will approach a stationary solution. Assuming that the model's parameters satisfy stationarity conditions,^[11] these equations may be solved to get a stationary solution for the Kalman filter weights.

Lemma: The stationary solution for κ_t is

where σ² is the stationary value for .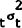

Proof: See the Appendix.

The vector of coefficients given in equation (18) contains the weights used to filter the unanticipated information that arrives at the end of period t, in order to calculate the best guess for the unobserved value of the true multiplier for the period just ended. Thus the agents' measure of the true money supply uses all available information, not just the measured aggregate, because they know that the unobservable measurement error is correlated with other observable variables. This projection in terms of observed variables may be transformed by using equation (12), into a relationship involving (observed linear combinations of) unobserved variables,

The information that arrives at the end of period t reveals the sum 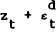, from equations (2) and (4), and the sum z_t + µ_t, from equations (8) and (4). Equation (19) shows that this information, appropriately weighted by variance ratios, is all that agents require to optimally update the expectations that they held at the beginning of the period.

Footnotes

See Chow (1975) for a presentation of the theory of Kalman filtering. [10]

The exact form of these stationarity restrictions will be seen later. [11]