RDP 1977-07: Money and the Balance of Payments 4. Results with the U.K. Model
October 1977
Before turning to the results of testing the five versions of the U.K. model, it is appropriate to give a brief description of the model's general theoretical structure.
4.1 The U.K. model
In addition to the three monetary sector equations, the model contains a core of nine equations which determine the rates of change of the flows of aggregate expenditure, output, imports, and exports, the levels of output prices and export prices, Bank Rate, aggregate tax receipts and the stock of domestic credit. Prices and interest rates are assumed to be “sticky” in the short run, adjusting only in the long run to equilibrium values determined in the rest of the world.[19] The time paths of asset stocks and commodity flows are therefore proximately determined by demand forces.
In general, the level of effective demand in each market is assumed to adjust to the difference between actual demand and its long-run partial-equilibrium level, although this is modified in the case of domestic expenditure to include a direct asset disequilibrium effect which captures the interdependence of decisions about expenditure on goods and accumulation of financial assets.[20] Stocks of financial assets, including money, adjust towards conventionally defined stock demands, while domestic expenditure adjusts to its equilibrium level implied by the levels of disposable income and interest rates, as well as to any disequilibrium in asset markets. Output and imports adjust, with different speeds, to their desired levels, which are in turn determined by the level of aggregate demand and the relevant relative price. Exports, on the other hand, are determined by world income and the price of U.K. exports (set by domestic producers) relative to world prices.[21] The change in international reserves is determined as the change in the quantity of money less the change in domestic credit, and this specification allows strong direct effects of money on the balance of payments.
The disequilibrium real balance effect on aggregate expenditure permits a direct effect of monetary disturbances on domestic commodity markets. There is no direct effect of monetary disequilibrium on prices, although output prices are responsive to pressures of demand in commodity markets and hence will be influenced through the expenditure mechanism by any disturbance to the money market. The most important of the secondary transmission mechanisms in the model is the effect of interest rates, which are represented by a policy reaction function for Bank Rate. It is assumed that the authorities use the rate primarily as a weapon for stabilising the level of international reserves,[22] although their decisions are also influenced by considerations of internal balance. The inclusion of reserve movements in the Bank Rate equation should assist in discriminating between the alternative hypotheses set out below, since it will make the model sensitive to the interaction of money and the balance of payments.
4.2 The results
The models outlined above, and an additional model, B*, which includes no direct channel
from domestic monetary disequilibrium to the balance of payments, are estimated with annual
U.K. data for the period 1885–1970.[23]
Model B did not converge in its original form, and it was necessary to constrain the
parameters on the war dummies in the 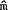 function; the values chosen are
those estimated in the B* version, which is also discussed below. In addition, the iteration
of Model E ceased on an almost flat portion of the likelihood surface, and thus failed to
converge; however, this problem is relevant primarily for comparisons of likelihood values
and does not affect the interpretatior of the parameter estimates.[24]
function; the values chosen are
those estimated in the B* version, which is also discussed below. In addition, the iteration
of Model E ceased on an almost flat portion of the likelihood surface, and thus failed to
converge; however, this problem is relevant primarily for comparisons of likelihood values
and does not affect the interpretatior of the parameter estimates.[24]
In general, the estimates have the expected signs and are significant by the usual t-test criteria. Each of the models, viewed as a particular set of constraints imposed on a (common) unrestricted reduced form, can be statistically rejected on the basis of a likelihood ratio test, but since the following discussion evaluates the relative performance of several basic theoretical models, this does not detract from the results. It would be futile to expect that a close fit to a long run of data could be provided by models as simple as those tested in the current section, although this does not rule out the possibility that the models adequately represent important systematic macroeconomic relationships. The tests reported below are designed to determine which among several economically meaningful models best fits the data.
Since estimates of the parameters in the core of the models are similar, the following discussion concentrates on the estimates of the monetary sector parameters, which are reproduced in Table 4.1.[25] These results indicate that domestic monetary disequilibrium has a strong direct effect both on domestic variables (as represented by the parameter γ1) and on the level of international reserves. However, the balance-of-payments offsets to excess money balances in both Models C and E are less well determined than the corresponding parameters in Models B and D.
The speeds with which asset markets adjust toward long-run equilibrium are found to be quite slow, and substantially less than the speeds of adjustment in commodity markets. This suggests, not only that frictions are important throughout the economy, but that they are particularly prevalent in asset markets, a finding not easily reconciled with those theories which emphasise rapid, if not instantaneous, adjustments in these markets. In particular, the estimates of α12 imply that there is an average lag of over ten years in the adjustment of money demand to money supply following an exogenous disturbance.
| Parameter\Model | A | B | C | D | E | B* |
|---|---|---|---|---|---|---|
| α10 | – | .031 (4.84) |
– | .027 (5.03) |
– | .044 (6.21) |
| α11 | – | – | .041 (1.74) |
– | .444 (1.86) |
– |
| α12 | .083 (5.58) |
– | – | .103 (5.48) |
.088 (4.16) |
– |
| γ1 | −.098 (4.66) |
−.069 (7.81) |
−.106 (3.52) |
−.092 (4.50) |
−.102 (3.89) |
−.083 (2.69) |
| γ4 | – | −.126 (6.52) |
– | −1.458 (3.44) |
– | – |
Table 4.2 presents the summary fit statistics for the six sub-models. It can be seen from these results that Models D and E perform better than Models B and C in a comparison of their simulation errors. Hence it appears that the flow disequilibrium models are preferred to the stock disequilibrium models on purely statistical grounds.
The results in Table 4.2 are less conclusive in evaluating the models where reserve changes are modelled directly as a function of monetary disequilibrium against those which include a behavioural relation for capital flows and determine reserve flows by adding up the components of the balance of payments. Models C and E give lower root mean square percentage errors than Models B and D for all three monetary sector variables, in non-dynamic simulations, and have the higher log-likelihood values. However, the dynamic simulation results do not clearly favour either specification.
| Model | A | B | C | D | E | B* |
|---|---|---|---|---|---|---|
| M – RMSPE1 | 2.7 | 3.9 | 2.5 | 3.8 | 2.6 | 4.3 |
| – RMSPE2 | 2.8 | 15.9 | 4.8 | 11.6 | 3.5 | 13.5 |
| R – RMSPE1 | 17.7 | 20.2 | 17.4 | 18.7 | 17.3 | 19.2 |
| – RMSPE2 | 21.6 | 69.0 | 17.5 | 37.7 | 20.2 | 41.7 |
| F – RMSPE1 | 28.8 | 30.5 | 29.2 | 29.9 | 29.3 | 29.4 |
| – RMSPE2 | 53.3 | 28.0 | 43.4 | 20.8 | 50.7 | 23.1 |
| Log-likelihood value | 3183.410 | 3136.132 | 3180.508 | 3161.373 | 3181.729 | 3122.178 |
| (394) | (392) | (394) | (391) | (393) | (393) | |
|
Log-likelihood value of unrestricted reduced form = 4019.468 |
||||||
Thus, although it is not possible to draw any definite conclusions from these results, they are encouraging in that the more structurally explicit models, in which the direct effects of excess money on the balance of payments are identified as working through capital flows, are not rejected by empirical testing.
It is possible, on the other hand, to reject Model A in favour of Model E, since the estimate of α11 in Model E is significantly different from unity, but set equal to unity in Model A. This implies that the balance-of-payments offset to flow disequilibrium in the money market is less than complete within the year; indeed, the average lag implied by the point estimate of α11 in Model E exceeds two years.
The existence of a direct external effect of excess money is strongly supported by an auxiliary test, which was to estimate Model B*, equivalent to Model B or Model D with γ4 set to zero, and hence including no direct channel from money to the balance of payments.
Although Model B* has a generally better simulation performance than Model B, it is inferior to Model D in both dynamic and non-dynamic tracking ability. Moreover, it can be rejected in favour of either Model B or Model D on the t-test of the significance of the parameter γ4 in the latter models.
Footnotes
The specification and estimation technique permit, in principle, these adjustments to occur instantaneously. Hence, unless the model is seriously misspecified, the degree of “stickiness” is determined by the data used. [19]
The asset disequilibrium is represented by a disequilibrium real balance term, which reflects the special role of money in a frictional economy. [20]
World income, prices and interest rates are proxied for estimation purposes by the relevant U.S. variables. [21]
Sayers (1976), pp.28 ff offers some support for this view in his discussion of the basis for Bank Rate decisions. The influence of internal balance, while unimportant in the period to World War II (see Pollard (1970), pp.14–17), has increased in the post-war period under the influence of Keynesian demand-management policies. [22]
The data sources and methods of construction of each variable are discussed in Jonson (1975). [23]
These convergence problems suggest that, even where two models are “nested”, a likelihood ratio test may not be accurate in discriminating between the models. Since other tests are available (e.g. the usual t-tests), the likelihood ratio tests are not used here, although they can be calculated by the reader. [24]
A complete set of estimates for all models is available from the authors on request. [25]
Figures in parentheses are asymptotic t-ratios. Note that the numerical values of the separate estimates of α11 and γ4 are not directly comparable; the other parameters are dimensionally equivalent. Estimates are generally similar to those reported in Jonson (1976). [26]
RMSPE1 denotes the root mean square percentage error from a one-period (non-dynamic) simulation over the full estimation period; RMSPE2 denotes the root mean square percentage error from a full dynamic simulation over the period 1955–1970. Figures in parentheses denote the degrees of freedom of each model, i.e. the number of restrictions which must be imposed on the unrestricted reduced form to obtain the structural model. [27]