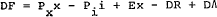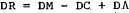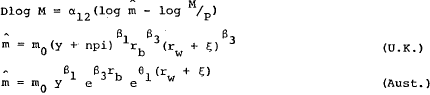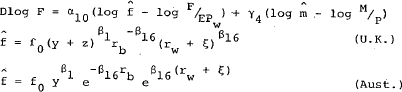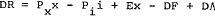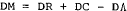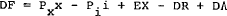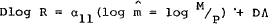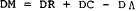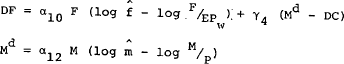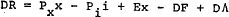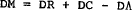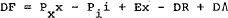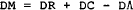RDP 1977-07: Money and the Balance of Payments 3. Alternative Specifications for the Monetary Sector
October 1977
The above discussion indicates that there are in the literature several approaches to the interaction of money and the balance of payments. Existing tests of these approaches, conducted with different data sets and estimation techniques, have not served to compare their relative merits, and it is therefore desirable to test each of the alternatives within a consistent and unified framework.
The strategy is to estimate the parameters of several structural models, each with a common core[12] and a monetary structure which depicts one of the alternative hypotheses about the channels by which monetary disequilibrium directly affects the balance of payments. Each monetary sector consists of three equations, determining the quantity of money, the balance of payments and the rate of net capital flows. These are described in turn.
A. The basic model
(10A) Net capital outflow
(11A) Change in international reserves
(12A) Quantity of money
This model retains the traditional assumption that the quantity of money is determined by a convergent first order adjustment process,[13] while the balance of payments adjusts automatically to the difference between changes in money and domestic credit expansion.[14] Capital flows are determined residually by the identity connecting the trade balance and the change in international reserves.
The mechanisms through which the quantity of money adjusts to money demand, however, are not explicit in this version of the model. Consider an exogenous change in domestic credit; this will cause an instantaneous change of equal and opposite magnitude in the level of international reserves (which will be associated with a capital outflow), leaving the money market unaffected. It is only when the second round effects begin to operate, primarily through the response of interest rates, that the equilibrium of the money market will be disturbed; and even then the dynamic adjustment is driven largely by fluctuations in money demand rather than the supply of money.
These comments suggest that equation (12A) should be interpreted as the reduced form of a set of (unspecified) whole-system feedbacks, and not as a behavioural relation. A specification of the monetary sector which has a more direct interpretation in terms of behavioural relations is set out below. It is similar to that already existing in the RBA76 model of the Australian economy, and might be interpreted as implementing more fully the view that money is a buffer stock in the short run.
B. Conventional balance of payments[15]
(10B)
(11B)
(12B)
This model uses a composite stock-adjustment hypothesis to determine net capital flows, in
which the first term represents the “normal” or longer-run influences on the
capital account, and the second term captures any short-run influence of stock
disequilibrium in the money market. The desired stock of net foreign assets,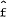 
, is assumed to
depend on a scale variable, real income, and the differential between domestic and foreign
interest rates, adjusted for the expected change in the exchange rate.[16]
The balance of payments is given by the trade balance less capital outflows, with adjustment
for exogenous transactions.
The most important difference between this and the previous model is in the system's response to an exogenous change in domestic credit. In the absence of the direct balance-of-payments offset present in Model A, the domestic credit disturbance will spill directly into the money market, with consequent impacts on domestic goods markets and capital flows; the magnitudes of the offset parameters will indicate the relative strength of the effects of such a monetary disequilibrium on domestic markets and the balance of payments. Furthermore, the mechanism by which the money supply is altered through changes in reserves is specified explicitly, while the model preserves the equality of money demand and money supply as a necessary long-run equilibrium condition.
A third alternative, which has been widely used as a characterisation of the monetary approach to the balance of payments,[17] is given in Model C, which simply states that international reserves will change if and only if there is a stock disequilibrium in the market for money.
C. Reserve flows a function of stock disequilibrium in the money market
(10C)
(11C)
(12C)
This specification, although broadly similar to that in Model B, assumes that the money market is adjusted directly through the balance of payments; much of this adjustment, however, occurs implicitly through capital flows, and so the model is open to the same criticism as Model A, that the monetary structure is obscured by the reduced-form nature of equation (11C).
The final alternatives considered in this paper differ from Models B and C by assuming that it is the flow disequilibrium in the money market, or more precisely the difference between the flow demand for money and the flow supply of money from domestic sources, which influences the balance of international payments. This hypothesis, which is derived as a fairly obvious generalisation of the initial work of Johnson (1972),[18] can be applied directly to either changes in international reserves or net capital flows, giving models directly comparable with Models B and C above.
D. Capital flows a function of flow disequilibrium in the money market
(10D)
(11D)
(12D)
E. Reserve flows a function of flow disequilibrium in the money market
(10E)
(11E)
(12E)
The definition of the flow demand for money in equations (10D) and (11E) assumes that the desired rate of change of the money stock is given by a first-order adjustment process on the stock disequilibrium in the money market; the flow demand for money is the product of the money stock and its desired rate of change. This specification is a generalisation of that in equation (12A), which assumes that the flow demand for money is equal to the actual change in the money stock; in the present model, however, the possibility that α11 differs from unity implies that a disturbance to domestic credit will create a stock disequilibrium in the money market rather than immediately being offset through the balance of payments. Hence, in the present specification the parameter α12 represents the desired, rather than actual, speed of adjustment of money balances to their equilibrium level, and the flow demand for money becomes an unobservable variable which must be estimated indirectly.
Since the properties of Models D and E are similar to those of B and C respectively, they need not be discussed again. However, it is worth noting that, in the case where α11 is unity, Model E becomes identical to Model A, as can be seen by substitution of (11E) into (12E) ; Model E can thus be interpreted as a generalisation of the basic model with which this discussion began.
Footnotes
The two core structures are described in Appendix
A, and the “monetary sector” equations described in this section
comprise equations (10) to (12) of each model.
It should be noted that this section treats F as net foreign assets owned by
domestic residents, which is the U.K. model definition. Since Australia has been a
net debtor on capital account, F in the RBA76 model is defined as net domestic
assets owned by foreigners. Thus in applying these models to the Australian case,
the appropriate sign adjustments are made.
Note also that the interest rate terms are entered in log-linear form in the asset
demand functions in the U.K. model, but in linear form in the Australian model.
[12]
While the simplification of a demand determined money stock is probably appropriate in fairly stable periods, it may be inappropriate for periods when supply disturbances are important. It should be noted that Jonson (1976) includes dummy variables for each world war in the demand for money function ; while these could be rationalised as representing uncertainty effects which raised money demand, it is less easy to rationalise in this way the tendency of the model to underpredict the quantity of money when it is simulated into the 1970's. [13]
The change in international reserves is also influenced by exogenous government capital flows and valuation effects, denoted by DΛ. Note that Λ is identically zero in the Australian case. [14]
In the remainder of this section, 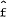and 
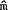are as
defined in equations (12A) and (10B) respectively.
[15]
The expected rate of change of the exchange rate, ξ, is modelled exogenously in the U.K. model as the forward discount on sterling (expressed as a percentage per year). In the Australian model, however, it is modelled implicitly as an endogenous variable; details of this construction are given in section 5. [16]
See, for example, the analysis of French and German macromodels by Sassenpour and Sheen (1976). This study also investigates a model similar to Model B, with α10 constrained to zero, and finds a significant direct disequilibrium real balance effect, estimated by a parameter analagous to γ4, on French capital flows. [17]
In the case when α10 is zero, this is similar to Johnston's (1976) interpretation of Porter's (1974) results for Australian capital flows as implying that capital flows respond rapidly, but not instantaneously, to the gap between the flow demand for money and the flow supply of money from sources other than capital flows. Porter assumed, however, that the money market was equilibrated in each period and thus that the flow demand for money is equal to the change in the stock demand; the present models do not impose this condition, but do in principle allow for it in the case where α10 is zero, α11 or γ4 is unity, and α12 is sufficiently large so that the stock of money is approximately equal to its desired level at all times. [18]