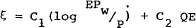RDP 1977-07: Money and the Balance of Payments 5. Results with the Australian Model
October 1977
Since the RBA76 model of the Australian economy is similar to the U.K. model in its general approach to the modelling of economic relationships, and has been described in detail elsewhere,[28] it will suffice here to indicate briefly the most important differences between the two models.
5.1 The Australian model
The greater structural detail of RBA76 is achieved in several ways: the disaggregation of expenditure into consumption and investment, and of taxation receipts into direct and indirect categories; a more complete modelling of domestic credit expansion; the addition of a distinct price deflator for public goods and services; and the inclusion of a market for labour. In addition, RBA76 endogenises the exchange rate through a policy reaction function, and takes explicit account of inventories in the market for commodities.
Exchange rate expectations, which are proxied in the U.K. model by the forward discount on sterling, are modelled implicitly in RBA76, as a function of the gap between domestic and world prices and an ex-post dummy variable, denoted QE, capturing the anticipation effects which are assumed to exist prior to any major change in the administered exchange rate.[29]
The transmission mechanisms from monetary disturbances to domestic variables are similar to those in the U.K. model. The secondary transmission mechanism through interest rates is preserved in the RBA76 reaction function for the bond rate, which includes variables representing both internal and external balance targets. The direct channel from monetary disequilibrium to domestic expenditure is important in the RBA76 model, which also allows for direct effects on domestic output prices, wages, and factor demands.
5.2 The results
The six sub-models are estimated with quarterly Australian data for the period 1959–1975.[30] Again, convergence problems were encountered in estimating some of the models, and so the likelihood values are not used as a basis for evaluating the alternative specifications. Table 5.1 summarises the estimates of the parameters of most immediate interest.[31]
| Parameter/Model | A | B | C | D | E | B* |
|---|---|---|---|---|---|---|
| α10 | – | .090 (6.68) |
– | .099 (7.38) |
– | .092 (7.07) |
| α11 | – | – | .565 (6.05) |
– | .166 (3.38) |
– |
| α12 | −.065 (4.43) |
– | – | .232 (1.29) |
.469 (2.37) |
– |
| γ1 | −.180 (4.61) |
−.262 (5.90) |
−.151 (4.52) |
−.248 (5.55) |
−.178 (4.68) |
−.273 (6.54) |
| γ4 | – | .114 (2.77) |
– | .040 (2.27) |
– | – |
| δ1 | −.174 (5.15) |
−.131 (4.60) |
−.167 (6.69) |
−.119 (4.54) |
−.236 (7.22) |
−.140 (5.10) |
| δ3 | −.224 (6.71) |
−.240 (6.46) |
−.234 (6.72) |
−.226 (6.01) |
−.253 (7.22) |
−.239 (6.34) |
The estimates have the expected signs, with the exception of α12 in Model A. In addition, the coefficients γ1, δ1 and δ3, which measure the influence of monetary disequilibrium on domestic consumption expenditure, output prices and money wages respectively, appear to be quite robust over the different monetary sector specifications. These domestic effects are estimated to be, in general, substantially larger than those in the U.K. model. The balance-of-payments offsets to domestic monetary disequilibrium are comparable in magnitude to the U.K. model results for the “stock” models B and C, but are substantially smaller for the “flow” models C and E.
Table 5.2 presents the summary test statistics for the monetary variables of each model. Comparison of static simulation errors suggests that Models B, B* and D provide a closer fit for the data than Models A, C and E. The dynamic simulation performance favour Model D over Models B and B*, and while it is difficult to distinguish Models B and B* on this basis, Model B* can be rejected on the grounds that γ4 differs significantly from zero in Model B and Model D.
In addition, Model A can be rejected in favour of Model E, since in the latter α11 is significantly different from unity on the usual t-test, and the negative estimate of α12 in Model A is not economically meaningful.
| Model | A | B | C | D | E | B* |
|---|---|---|---|---|---|---|
| M – RMSPE1 | 1.1 | .6 | .7 | .7 | .7 | .7 |
| – RMSPE2 | 7.8 | 4.8 | 4.2 | 4.6 | 3.0 | 5.1 |
| R – SMSPE1 | 8.3 | 5.4 | 5.5 | 5.4 | 5.6 | 5.3 |
| – RMSPE2 | 32.7 | 18.4 | 20.0 | 16.9 | 27.9 | 17.7 |
| F – RMSPE1 | 5.3 | 1.8 | 3.7 | 1.6 | 4.5 | 1.8 |
| – RMSPE2 | 42.0 | 8.6 | 30.9 | 7.4 | 44.2 | 8.8 |
| log-likelihood value | 7137.306 | 7284.948 | 7191.756 | 7260.693 | 7159.548 | 7282.209 |
| (1,112) | (1,107) | (1,112) | (1,106) | (1,111) | (1,108) | |
|
Log-likelihood value of unrestricted reduced form = 18966.420 |
||||||
Overall, the results of testing the alternative specifications in the RBA76 framework are similar to those for the U.K. model. The adjustment speeds in asset markets are, in general, low relative to lags in the goods market, although in general adjustment speeds are more rapid than those implied by the U.K. model estimates. More importantly, the existence of a direct balance of payments offset to domestic monetary disequilibrium is supported by the empirical results, and the preferred specification of this effect has the flow disequilibrium in the money market influencing the rate of net capital inflow. This last conclusion is somewhat stronger than that for the U.K. model, since in that framework Model D could not be clearly distinguished from Model E on the available bases for comparison.
Footnotes
The early development of the model is documented in Jonson, Moses and Wymer (1976). The current version is given in full in Appendix A. [28]
The data sources, and methods of construction, are given by Jonson, Moses and Wymer (1976); the complete set of parameter estimates is available from the present authors on request. Since the Australian data are quarterly and the U.K. data annual, the estimates of the adjustment speeds αi and μi (i.e. those parameters which have a time dimension) from the RBA76 model must be multiplied by four for direct comparison with the corresponding... [30]
Other parameters in the models are generally similar to those in other versions of the RBA76 model. [31]