Research Discussion Paper – RDP 2025-02 Boundedly Rational Expectations and the Optimality of Flexible Average Inflation Targeting
April 2025
1. Introduction
There is agreement among economists that expectations are central to monetary policy design. However, there is disagreement over how to model expectations, and prescriptions about the optimal conduct of monetary policy can be sensitive to assumptions about expectation formation. We formulate a general framework for expectation formation that nests or approximates alternative expectation theories. We use this general environment to derive optimal target criteria under commitment for a welfare-maximising central bank given different assumptions about the constraints that it faces, such as an inability to observe contemporaneous economic conditions or the zero lower bound (ZLB) on nominal interest rates. We characterise the dependence of optimal policy prescriptions on features of the expectation formation process and provide recommendations that are independent of how expectations are formed.
We find that if a central bank can credibly commit to a path for the policy rate, then the optimal target criterion for a wide range of expectation formation theories is always a form of flexible average inflation targeting (FAIT). We show that the average in FAIT should be a weighted average of current and past inflation with declining weights over time. Monetary policymakers should respond most forcefully to current inflation, while also committing to partially ‘make up’ for past inflation misses. But the weighted average inflation target is also flexible because when a policymaker's ability to achieve this target is in question, it should seek to influence expectations more aggressively than usual. A policymaker should commit to stronger-than-usual make-up policy when they are unable to control the output gap to implement the current target, such as when they have imperfect information about the state of the economy or the ZLB binds. In addition, they should pre-emptively deviate from the target to steer expectations favourably when they anticipate future constraints, such as drifting inflation expectations or the ZLB. Especially with respect to the ZLB constraint, policy is a ‘use it or lose it’ proposition for all the expectations theories that we capture.
Central to understanding the advantage of a FAIT policy is recognising a symmetry between (i) the history dependence that a central bank should optimally commit to when agents' expectations are near the full information rational expectations (FIRE) benchmark, and (ii) the history dependence in agents' own expectations that emerges under adaptive learning. In the former case, it is optimal to manage agents' expectations by committing to make up for past misses to targets by setting current policy based on a weighted average of past outcomes. In the latter case, it is optimal to respond preemptively to expected future outcomes by influencing agents' expectations, which are themselves a weighted average of past outcomes.[1] In both cases, optimal policy requires flexible deviations from the weighted average target to more aggressively influence expectations when policy is constrained. Therefore, despite the different rationales for policy in each case, the optimal policy shares several key features.
Our agnostic approach to expectations allows us to derive a more broadly applicable optimal policy framework, encompassing much of the existing literature's results, while also characterising novel environments not yet explored. Specifically, we model expectations as a weighted average of adaptive learning and FIRE, where the rational expectations take into account the learning expectations, and where the desired path of the policy rate is credible and known to all. We show that by varying the weight placed on rational expectations relative to learning, and by varying the speed of the learning, that we capture relevant dimensions of several types of expectation formation models within a standard New Keynesian economy. The expectation models include adaptive learning as in Evans and Honkapohja (2001) and Preston (2005), behavioral expectations as in Gabaix (2020), and key elements of level-k reasoning as in Angeletos and Lian (2018), Farhi and Werning (2019), Angeletos and Huo (2021) and Evans, Gibbs and McGough (forthcoming). Each of these different expectations models lies as a special case that we can recover or closely approximate within our more general setting, and allows for characterisation of optimal policy in novel settings.
The general target criteria that we derive constitute a formal theory for a FAIT policy framework. We start from the primitive that monetary policy has a statutory mandate to stabilise inflation and real activity. Policy, therefore, seeks to minimise a loss function over squared deviations in inflation from a target and squared deviations in the output gap, which captures the welfare theoretic loss function for the representative household. The general target criterion we derive for this loss function consists of two distinct pieces: 1) a weighted-average inflation target (WAIT), and 2) prescriptions for flexible deviations from WAIT that change based on the speed of learning or the constraints faced by the central bank. In the weighted average part of FAIT, the weights that a policymaker places on current versus past observations are determined by how rational private sector expectations happen to be and decline geometrically over time. When there is learning, optimal policy requires flexible deviations from what is implied by WAIT alone. The effect of shocks and policy today may be extrapolated far into the future beyond their natural or intended duration. This creates the rationale for deviating from the policy implied by past data alone to pre-empt expected deleterious drifts in agents' expectations caused by shocks, or to pre-emptively generate favourable drifts in expectations through policy.
Flexible deviations from WAIT are also required when information constraints or the ZLB prevent the central bank from implementing its desired level of demand in the economy. In these situations, again, the central bank should be flexible by more aggressively steering expectations. It should commit to stronger make-up policy than usual, and it should act pre-emptively to influence expectations if it expects the ZLB might bind in the future. This is the rationale behind forward guidance policy in Eggertsson and Woodford (2003), where under FIRE the promise of future policy alleviates the constraints on policy today. We show that this type of policy is desirable regardless of how inflation and output expectations are formed.
We demonstrate the robustness of the shared features of optimal policy by running two horse races comparing a range of different inflation and output gap policy targets. We first show that we can approximate the optimal target criteria using simple weighted-average criteria over past inflation and output gap outcomes, which are superior to price-level targeting, inflation targeting, or arithmetic average inflation targeting using a fixed window when agents are boundedly rational. We then compare how these competing criteria perform when policymakers do not know how expectations are formed. Specifically, we choose a single calibration for each different target criteria to maximise average welfare across different economies with expectations ranging from FIRE to full adaptive learning. We find that simple implementations of FAIT that target geometrically declining averages of inflation (WAIT) and the output gap (which captures some aspects of flexibility required in optimal policy) are the most robust, generating similar losses to the fully optimal policy regardless of how expectations are formed.
1.1 Literature review
We take a novel approach to the study of FAIT by using target criteria. Much of the policy work on this topic has focused on the study of modified interest rate rules that include averages of past inflation as arguments. For example, papers cited in strategy reviews by the Federal Reserve (e.g. Arias et al 2020), European Central Bank (e.g. Work Stream on the Price Stability Objective 2021) and Bank of Canada (e.g. Dorich, Mendes and Zhang 2021) have taken this approach.
There are several drawbacks to interest rate rule-based analysis. Svensson and Woodford (2005) argue that interest rate rules are a fragile and non-transparent way of specifying a policy framework.[2] Interest rate rules are model specific and the mapping between policy framework and an interest rate rule is not clear cut. In some cases, different rules can generate the same equilibrium outcomes. For example, Eskelinen, Gibbs and McClung (2024) show that unconditional optimal policy in the standard New Keynesian model can be implemented with an interest rate rule that responds to a lagged interest rate term, similar to interest rate smoothing, or to a weighted average of past inflation, similar to some average inflation targeting specifications in the literature. In other cases, slightly different rules generate drastically different equilibria. For example, Honkapohja and McClung (2024a) point out several examples of the fragility of interest rate rule specification that try to capture average inflation targeting (AIT) under rational expectations and adaptive learning. They show that small changes to the number of periods included in the inflation average can lead to drastically different policy outcomes. It is therefore difficult to draw robust conclusions about policy frameworks from a comparison of interest rate rules.
In contrast, target criteria are general. They do not depend on the statistical properties or the number of economy-wide shocks that the central bank faces. They depend only on how beliefs are formed and on the constraints the central bank encounters when implementing its desired policy. In addition, policy is specified as a target for endogenous variables, that is, a set objective for the evolution of economic outcomes policymakers hope to achieve. Target criterion are inherently less constraining than interest rate rules because they allow (subject to the ZLB) any choice for the path of policy rate necessary to achieve their goals. Communication of policy in such a framework is, therefore, forward looking and data dependent, which reflects the way policymakers actually communicate.
Optimal target criteria for both unconstrained and constrained policymakers have been widely studied under FIRE. The theoretical justification for inflation targeting (e.g. Giannoni and Woodford 2005), price level targeting (e.g. Giannoni 2014) and inflation forecast targeting (e.g. Svensson and Woodford 2005) policy frameworks rest on this work. In addition, Eggertsson and Woodford (2003) extend optimal target criteria to the case of optimal policy at the ZLB, and others have studied optimal policy under imperfect central bank information (e.g. Clarida, Galí and Gertler 1999; Woodford 2010). We extend these works by studying a more general model of expectations. We show that some conclusions from the FIRE analysis are knife edge. Small departures from the FIRE assumption imply a new optimal policy framework: FAIT.
Optimal target criteria for an unconstrained policymaker have been studied in the adaptive learning literature, such as in Molnár and Santoro (2014), Eusepi et al (2018) and Eusepi, Giannoni and Preston (2024). These papers establish that optimal policy shares some features with the optimal target criterion from the FIRE analysis, in which it is optimal to engineer periods of price level overshooting or make-up policy in certain circumstances. We extend these works by approximating them within our general model of expectations and by deriving optimal target criteria in settings with imperfect information and the ZLB. We show that the similarity in optimal policy under both adaptive learning and FIRE carries over to other general forms of bounded rationality, and can be captured by a FAIT policy framework.
A related set of studies derive optimal target criteria in the unconstrained case under other kinds of deviations from FIRE. Gabaix (2020) and Benchimol and Bounader (2023) derive optimal policy when agents have myopic expectations and over-discount the future. In Dupraz and Marx (2023), agents have finite planning horizons and are similarly myopic, but also learn about long-run outcomes, which adds a backward-looking component to expectations. Gasteiger (2014) and Gasteiger (2021) analyse optimal policy in a heterogeneous expectations setting, where some agents have rational expectations and others are adaptive.[3] We can approximate the key elements of these models for expectations within our general framework, and extend the optimal policy analysis by deriving optimal target criteria in the constrained case, when the central bank has imperfect information or the ZLB can bind.
Outside of the unconstrained case, there are several papers that explore optimal policy at the ZLB in non-FIRE settings. Eusepi, Gibbs and Preston (2024) and Evans et al (forthcoming) both study optimal forward-guidance policy when agents must learn about the general equilibrium implications of policy. The former takes an adaptive learning approach, while the latter combines adaptive learning with level-k thinking. Dupraz, Le Bihan and Matheron (2024) analyse make-up policy when agents have finite planning horizons. Budianto, Nakata and Schmidt (2023) allow for both FIRE and a Gabaix (2020) style of myopic expectations, and compare delegated loss functions for a central bank optimising under discretion. In contrast to these papers, we derive optimal target criteria under commitment analytically, which shows that a particular kind of FAIT framework can capture the features of optimal policy at the ZLB that this prior work explores.
Our general framework also lets us approximate other models for expectations that feature some kind of myopia and a backward-looking learning process, for which optimal target criteria have not been derived. For example, Angeletos and Lian (2018), Farhi and Werning (2019) and Angeletos, Huo and Sastry (2021) all propose models with some combination of level-k reasoning, heterogeneous private information, and/or learning. Importantly, we characterise the unconstrained, imperfect central bank information, and ZLB cases under all of these different expectations assumptions. Because our framework nests a range of different specifications, we are also able to find the robustly optimal policy framework, in circumstances where policymakers do not know the true model for expectations.
Finally, there is a related adaptive learning literature that examines whether optimal target criteria derived under FIRE generate equilibria that are learnable. This literature finds that it depends on how the optimal target criteria is implemented. Optimal target criteria do not imply unique interest rate rules. Evans and Honkapohja (2003), Preston (2006), Orphanides and Williams (2007) and Evans and McGough (2010) show that different interest rate rules that react to different endogenous quantities, which implement the same equilibrium under FIRE, may have different stability properties under least squares learning. Honkapohja and Mitra (2020) study price level targeting under learning and varying credibility. The optimal targeting criteria we study here, however, are derived taking learning into account as a constraint, making expectational stability an endogenous concern of the policymaker. Our robust policy analysis finds versions of the FAIT framework that ensure expectational stability even when the policy rule is misspecified.
2. The Model
We study the standard New Keynesian environment of Woodford (2003) with sticky prices and monopolistically competitive firms. However, we depart from the standard environment by assuming that expectations need not be rational and may encompass a wide range of beliefs formation strategies. To accommodate this generality, we log-linearly approximate aggregate output and inflation dynamics as
where xt is the output gap, is inflation, it is the nominal interest rate controlled by the central bank, is an exogenous real rate of interest (which could reflect movements in demand and productivity), ut is a cost-push shock, and represents potentially non-rational expectations. Equation (1) is the infinite-horizon IS curve, which captures household demand under arbitrary beliefs. Under FIRE, this equation collapses to the familiar two-period representation. However, the form here distinguishes the effect of longer-term income and real interest rate expectations on consumption decisions, which are critical when the central bank is constrained in the present.[4]
For Equation (2), the Phillips curve, we use the common two-period approximation, which approximates the effect on pricing decisions of expected inflation and output gaps in all future periods using just the one-period-ahead inflation expectation. Appendix C.1 provides the full infinite-horizon form of the Phillips curve (also called the anticipated utility solution in the adaptive learning literature; under FIRE, it is equivalent to the two-period form), and Appendices C.2 to C.5 replicate all of our main results in that setting. We choose to use the two-period approximation for the Phillips curve in the main analysis because the key results are not sensitive to the choice (in contrast to the choice of IS curve representation) and are easier to interpret. It also allows us to more closely nest/approximate the reduced-form Phillips curve formulations of the myopia and anchoring model of Angeletos and Huo (2021), the hybrid New Keynesian Phillips curve, and older works in the adaptive learning literature such Evans and Honkapohja (2003) and Molnár and Santoro (2014).
Beliefs of the private sector. We put forward a general notion of belief formation. We do not intend for our formulation to be a theory of expectation formation on its own; however, many papers have done so using similar approaches, such as in Brock and Hommes (1997), Branch and McGough (2009) and Cole and Martínez-García (2023). Our goal is to write beliefs in such a way that for specific calibrations we recover distinct expectation theories put forward in the literature.
We assume that some fraction [0,1] of agents possess FIRE, and a fraction 1 – are adaptive learners, in that they use a statistical model to forecast future outcomes by extrapolating from past observations.[5] Aggregate expectations of future inflation and output gaps are
where is the FIRE forecast and denotes the learners' forecast.
We assume that adaptive learners forecast inflation and the output gap using an unobserved components state-space model, which they estimate using a steady-state Kalman filter. Inflation and the output gap are assumed to be driven by an unobserved persistent component, with an autoregressive coefficient of , and an iid component. Learners use observations up to period t – 1 to estimate the persistent component, where , denotes period t's state estimate. Learners use this estimate to forecast future variables . Their expectations for and , are therefore given by
where the steady-state gain coefficient g reflects their beliefs of the relative variance of the perceived unobserved persistent and transitory shocks in the state-space model. This procedure implies the updating rules
We assume for simplicity that the parameters relevant for beliefs – and g – are the same for both households and firms, and for both inflation and the output gap.
For expectations of the nominal interest rate, we assume that everyone has rational expectations over its path.[6] This is equivalent to assuming that the policymaker communicates its expected policy rate path each period, and that path is believed by all agents. The distinction between the formation of nominal interest rate expectations and the formation of output gap and inflation expectations is common in the existing literature on make-up policy.[7] If the policymaker communicates its expected path for the nominal interest rate, then this path is immediately available to households and firms, whereas determining the future output gap and inflation implications of that path involves much more sophisticated general equilibrium reasoning. Even if the central bank's communication of its interest rate expectations is not perfect, the effect of interest rate expectations on household decisions will often flow through fixed rates and asset prices, which are determined by sophisticated financial market participants who are highly forward looking and likely to form similar expectations to the central bank.[8]
Beliefs of the policymaker. We assume throughout that the central bank possesses FIRE and seeks to maximise the standard welfare function
which is a quadratic approximation to household welfare when When choosing policy, the policymaker takes household decisions and beliefs as constraints:
The policymaker's problem. The optimal policy problem is to choose the sequence that maximises the welfare function (9) subject to the constraints (10) to (13) imposed by private sector equilibrium behaviour. We assume that the policymaker is credible and pursues optimal policy from a timeless perspective, in that they do not seek to exploit the exogeneity of the initial conditions. Instead, the policymaker in the initial period acts according to the rule that would have been optimal had they committed to it in advance.[9]
Nesting/approximating other models. The pay-off for the particular way we model beliefs is in nesting the structural equations implied by most of the prominent expectations theories in the literature. For example, when
- FIRE : the system reduces to structural equations implied by full information rational expectations:
- myopia and level-k (0 < < 1 and g = 0): the system reduces to a model that is ‘over-discounted’ such as in Angeletos and Lian (2018) or Gabaix (2020):
- hybrid New Keynesian Phillips curve (0 < < 1 and g = 1): the system reduces to a model with a hybrid New Keynesian Phillips curve, or one that features elements of myopia and anchoring as in Angeletos and Huo (2021):
- adaptive learning ( = 0 and 0 < g < 1): the system reduces to a model of adaptive learning:
By nesting these competing assumptions, we can compare optimal policy within a shared framework.
3. Optimal Policy – The Unconstrained Case
We start with the unconstrained optimal policy problem given by Equations (9) to (13). The policymaker is free to choose any policy today and into the future that they would like. Appendix A.1 contains the full derivations for all results; here we summarise the key equations to build intuition.
Monetary policy in this case is a powerful tool even with bounded rationality because the path of interest rates is common knowledge. If the central bank only faces the demand shock, then it is able to perfectly stabilise the economy as in the standard FIRE case.
Result 1 (IS curve irrelevance). The IS curve is not a constraint when the path of interest rates is known and credible. Demand shocks (and other shocks that do not affect the gap between the efficient and flexible-price levels of output, such as productivity shocks) may be perfectly offset with current and promised changes in the interest rate, generating no welfare loss.
The trade-off for the central bank, therefore, lies with ‘cost-push’ shocks (i.e. shocks that do affect the gap between the efficient and flexible-price levels of output).
To characterise optimal policy for cost-push shocks, we take the first-order conditions with respect to and xt for the central bank's policy problem and eliminate the Lagrange multiplier on the Phillips curve:
where L is the lag operator and is the Lagrange multiplier on the updating rule for learners' inflation expectations. The term represents the benefit of increasing learners' inflation expectations and is determined by the first-order condition with respect to :
Solving Equation (15) for gives
where and and are the roots of the characteristic polynomial associated with Equation (15).[10]
Result 2 (Unconstrained optimal target criterion). The optimal target criterion is
which is composed of two distinct parts:
- a weighted-average inflation target (WAIT)
- pre-emptive policy actions based on expected future trade-offs between inflation and output gaps due to drifts in learning beliefs.
The WAIT term represents a commitment to the forward-looking rational agents. The policymaker promises to adjust the output gap in response to a weighted average of past inflation. Shocks today that generate misses in the inflation target imply future policy adjustments, lessening the equilibrium impact of any shock.
The pre-emption term represent the management of backward-looking adaptive learning expectations and is present if g > 0. The policymaker forms a belief about how inflation expectations are likely to evolve in the future given current and past misses in inflation, which are propagated through the adaptive learning component of beliefs. Drifts in inflation change the trade-off between future inflation and output gaps. Additional policy today can pre-empt future undesirable movements in this trade-off, or engineer more favourable ones.
A key feature of the optimal target criterion (17) is that it encapsulates the target criteria from a range of different primitive assumptions about how agents form beliefs as special cases. Table 1 summarises the target criterion for the special cases discussed in the previous section. Optimal policy in this case is WAIT + pre-emption. The table, however, includes a fixed belief case of = 0 and g = 0, which is of interest because it recovers the same target criterion that is implied under FIRE for discretionary policy. This case reveals that so long as expectations can be influenced, that is, g > 0 and/or > 0, it makes sense to deviate from the standard FIRE optimal discretion policy, that is, from inflation targeting.
| Case | Target criteria | Policy |
|---|---|---|
| FIRE, = 1 | = – pt | PLT |
| Hybrid NK PC, 0 < < 1, g = 1 | Equation (17) | WAIT + pre-emptive |
| Myopia/level-k, g = 0 | WAIT | |
| Adaptive learning, = 0 | IT + pre-emptive | |
| Fixed beliefs, = 0, g = 0 | IT | |
| Notes: Optimal target criteria in special cases. No terms from optimal target criteria drop out for Hybrid NK PC (New Keynesian Phillips curve) parameters. PLT stands for ‘price level targeting’; IT stands for ‘inflation targeting’. | ||
3.1 Mechanics of optimal policy
To see how policy works in practice in response to a shock, let the cost-push shock follow a first-order autoregressive process such that EtuT depends only on ut for . Recall from Equation (16) that the Lagrange multiplier on learners' inflation expectations is a function of past and current expectations of inflation at different horizons. In Appendix A.1, we show that, in the optimal equilibrium solution, this multiplier can be written
for some positive constants ax, and au. Sensibly, optimal policy aims to lower learners' inflation expectation when inflation itself is high, when their expectations are high, or when the cost-push shock is positive. This desire for lower inflation though is tempered by a desire to close the output gap, which gives rise to the positive relationship with xt. Using Equation (18), we can write the optimal target criterion (17) (in equilibrium) as
where and .
Equation (19) reveals that optimal policy adjusts the output gap in response to an exponentially weighted average of current and past inflation, , and cost-push shocks, where the weight on lag j is . In addition, relative to FIRE, the central bank increases its response to current inflation while also responding to learners' inflation expectations – pre-emption – because both affect future inflation due to drifting inflation expectations. The central bank also must respond separately to the cost-push shock ut (beyond its effect on current inflation). How aggressive or accommodative policy is with respect to past inflation, expectations, or the shock depends on and g, that is, how quickly these interventions show up in expectations.
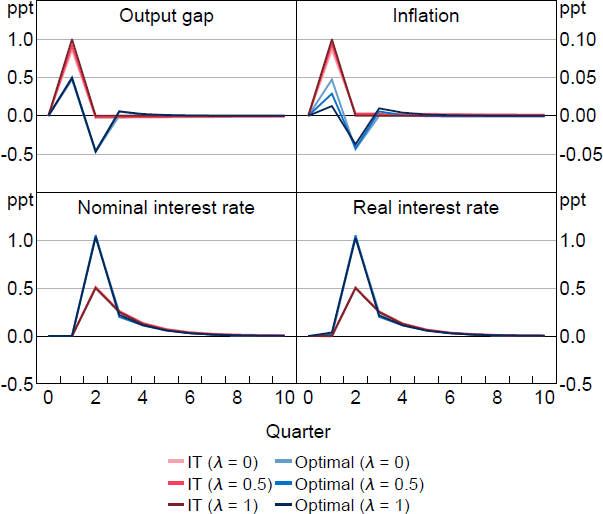
Figure 1 shows the optimal response to a cost-push shock as is varied compared to policy under an inflation-targeting (IT) regime ( and ). IT here is equivalent to the optimal targeting criteria implied under rational expectations discretion.
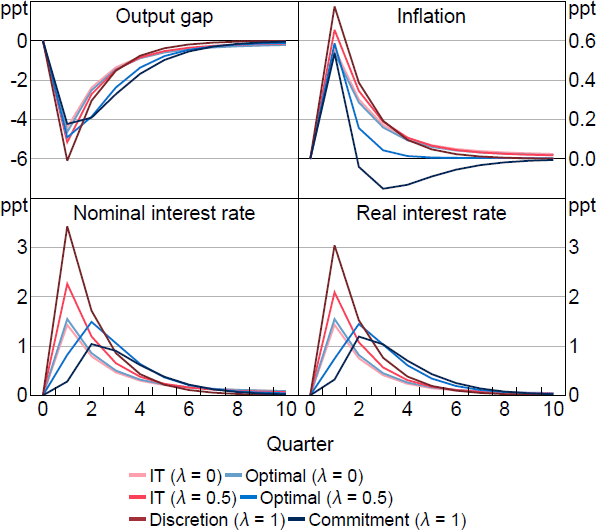
Notes: Response to a 1 per cent cost-push shock, which occurs in period 1. Parameter values are = 0.95, g = 0.08, = 0.99, = 1, = 0.1, /7.87.
Optimal policy for a wide range of s implies initially a muted response followed by a more aggressive policy in the medium run compared to IT. In the high cases, policy reflects the make-up quality of WAIT. Higher inflation now means a higher interest rate in the future even as inflation falls. The expectation of this policy is capitalised into current expectations blunting the impact of the shock and lessening the need to initially raise interest rates aggressively.
In the low cases, policy reflects the different way a shock propagates when there is learning. Backward-looking agents' expectations are less sensitive to the shock on impact because their expectations are anchored to the past. This means the shock has less of an impact initially, which allows for a muted interest rate response by policymakers. However, the learning process endogenously propagates the shock as expectations are revised. This leads to a growing inflation impulse over time because of rising . The optimal policy response to this growing impulse is a higher interest rate in the medium run to constrain inflation and output. The optimal policy, therefore, for a wide range in follows the same prescription: muted on impact and more aggressive over the medium run. This is true even though the rationale for why the central bank should enact such a policy changes as is varied.
Optimal policy only departs from this pattern when is close to zero. Here, the WAIT term is nearly absent and pre-emption is the dominant feature of policy. Stronger policy is required in these cases initially to blunt the propagation of the shock in beliefs. This represents the flexibility required by optimal policy in FAIT. If a policymaker expects expectations to drift, that is, become unanchored, in response to a shock, then more aggressive policy is required now.
For moderate values of , however, the pre-emption motive is secondary to WAIT. Figure 2 illustrates how pre-emption affects policy when = 0.5 as we vary g making expectations more or less responsive to the shock. The figure shows WAIT ( and ) compared to optimal policy. The difference between WAIT and optimal policy is pre-emption. The WAIT policy delivers lower interest rates and real rates in each case. Pre-emption on the other hand increases the current response as g increases to counter the greater influence of the shock in causing drifts in learned expectations.
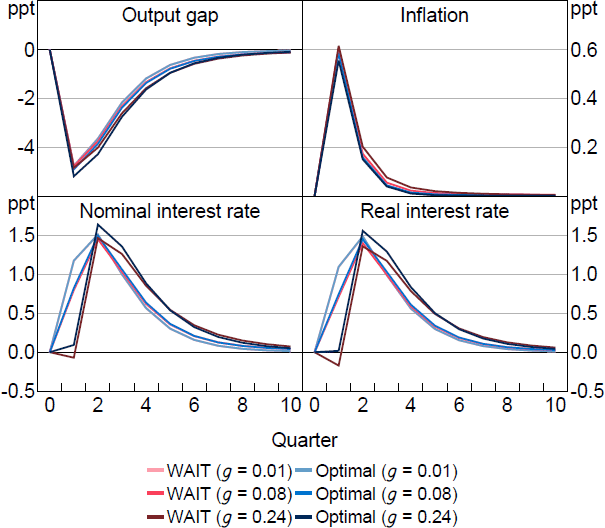
Notes: Response to a 1 per cent cost-push shock, which occurs in period 1. Parameter values are = 0.5, = 0.95, = 0.99, = 1, = 0.1, /7.87.
There are of course other scenarios where even with moderate values of pre-emption becomes more central. For example, when shocks are very persistent or the central bank expects to be constrained in the future such as when the ZLB binds, which we explore in Section 4.
3.2 The optimal average inflation target
The continued importance of WAIT relative to pre-emption shown in Figure 2 when is small is surprising. The reason it occurs is that the expectations of adaptive learners in our set-up evolve as a weighted average of current and past inflation,
Pre-emption, therefore, is an optimal response to a weighted average of past inflation. It turns out that that weighted average implied by the pre-emption component of optimal policy in equilibrium shares many features with the original WAIT component of optimal policy. In fact, it is possible to rewrite optimal policy as a simple WAIT policy with different weights that share a similar geometric decay over time.
To illustrate, substitute the weighted-average expression above for adaptive learning beliefs into the rewritten optimal target criterion (19) and rearrange:
where . The average inflation measure that a policymaker should target is a weighted average of two exponentially weighted averages of current and past inflation.
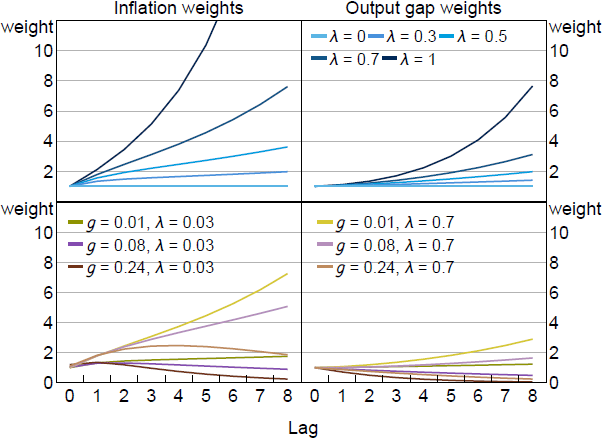
Figure 3 illustrates the similarities in the weights by plotting the term in front of from Equation (20) for different values of and g. On the left side, we plot the optimal weights for different values of when g = 0 and = 0. This calibration reflects models with myopia like Gabaix (2020) and it has no pre-emption component to policy. The high weight placed on current inflation reflects , the welfare weight on the output gap, which here is set to the welfare theoretic value of . Higher values of scale these weights profiles down while lower values raise them. When = 1, we have the optimal policy under FIRE: price level targeting. Equal weight is given to all past inflation outcomes. When = 0, there is no value to commitment and we get the rational expectations discretion outcome.
On the right side of Figure 3, we add a positive gain (g > 0) activating the pre-emption term. The optimal target criterion again responds to a weighted average of inflation. Pre-emption causes the weights to be higher depending on the specific level of g and . However, the general profile of the weights remains the same with a geometric decline over time. Optimal policy tracks a qualitatively similar weighted average of inflation when most agents have FIRE expectations and when most do not. In Section 5, we consider whether there is a single calibration for this weighted average that performs well regardless of how expectations are formed.
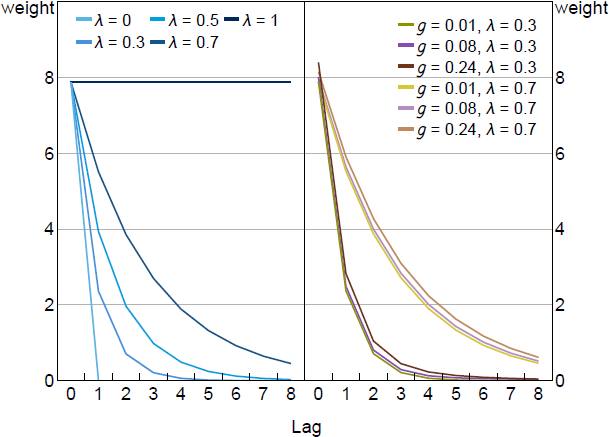
Notes: Plots coefficients in the power series in the first term of Equation (20), which represent the weight placed on current and lags of inflation when implementing optimal policy. Parameter values are = 0.95, = 0.99, = 0.5, = 0.1, /7.87.
In addition, it is important to note that the profiles of optimal weights are very different to the arithmetic averages that many researchers have studied when modeling average inflation targeting such as in Eo and Lie (2020) or Honkapohja and McClung (2024b). Arithmetic averages imply uniform weights over a fixed number of lags and zero thereafter. We show in Section 5 that arithmetic averages do a poor job approximating the optimal weights, while simple geometric averages approximate optimal weights well, even when the geometric weights are significantly misspecified relative to the optimal weights.
4. Optimal Policy – The Constrained Case
We now turn to the case where the policymaker faces a constraint that prevents it from implementing a desired level of the output gap period by period. We consider two ways in which this might occur: 1) imperfect information, and 2) the zero lower bound on nominal interest rates. Again, Appendix A.2 provides detailed derivations, while we focus here on the key equations and intuition.
4.1 Imperfect central bank information
Let denote the central bank's information set in period t and let It denote the full information set. Let zT|t denote the best estimate of any variable zT conditional on , while continues to denote the expectation conditional on the full information set It. We now assume
In other words, the central bank does not possess all information in the current period necessary to implement optimal policy. The nominal interest rate it must be set each period based on incomplete information , that is,
For our purposes, it does not matter what information is missing. The key is that any missing information relevant to policy represents a constraint on current policy choices.
The optimal policy problem is to choose the sequence that maximises the welfare function (9) subject to the constraints (10) to (13) imposed by private sector equilibrium behaviour and the informational constraint (21).[11]
The first-order condition of the policymaker's problem with imperfect information with respect to it is
where is the Lagrange multiplier on the information constraint (21). Condition (22) shows that the benefit of lowering the nominal interest rate is given by the benefit of raising the output gap in the current period, and in previous periods through the fact that agents anticipate future policy responses. Condition (23) shows that the central bank should try to set the nominal interest rate so that there is no benefit to increasing or decreasing it, given the information on hand. The main difference from the unconstrained case is that demand shocks are no longer irrelevant.
Result 3 (IS curve relevance). The central bank cannot perfectly offset shocks to the IS curve when .
In the unconstrained case, when , then and so . A shock to the IS curve is irrelevant. When , the best the central bank can do is , and so and in general, which makes the IS curve a constraint on policy.
To see how this affects optimal policy, we take the expectation of (22) conditional on and using for all gives
which implies that the central bank commits to an it that balances the estimated costs of an off-target output gap in period t, , against the reduced losses in the periods before t due to expectations of . Equation (24), therefore, describes a new intertemporal trade-off, where the central bank cannot set the desired interest rate it would like, ex post, while considering ex ante how its corrections for any errors it makes interact with private sector expectations.
Taking the first-order conditions with respect to and xt, eliminating the Lagrange multiplier on the Phillips curve, and substituting in from (22) gives
which generalises Equation (14).
The information constraint implies three additional terms. The new term in on the left-hand side is zero in expectation and represents the extent to which a shock causes the central bank to ‘miss’ its intended target for the output gap. The first new term on the right-hand side – in – is an additional commitment requirement of optimal policy. It indicates how the central bank should respond to past misses caused by unexpected shocks, that is, additional make-up policy. The commitment to respond to misses in the future shifts current expectations, thereby dampening the costs of the shock. In this way, commitment under imperfect information acts as a kind of ‘automatic stabiliser’. Finally, the Lagrange multipliers on learners' inflation and output gap expectations are now
The new components in these expressions, that is, the terms in , dampen the extent of optimal make-up policy, by accounting for its effect on learners' future expectations.
Substituting the Lagrange multipliers (26) and (27) into (25), we can derive the optimal target criterion under information constraints.
Result 4 (Information constrained optimal target criterion). Recall from Equation (17) that the optimal target criterion under full information is , where is defined as
Then the optimal target criterion under imperfect central bank information is
with and
The optimal target criterion under imperfect information (28) generalises the unconstrained target criterion (17). It differs from (17) in two ways: (i) the central bank does its best to implement it given its information set (i.e. it can only control , not ), and (ii) its target for is not always zero, but adjusts based on past errors in implementing optimal policy – – due to the information constraint.
The optimal target criterion though remains a flexible average inflation target. The difference here is in the definition of flexibility. The central bank still retains the same WAIT and pre-emption incentives but now must commit to make up for any errors in implementing policy that arise from the information constraint.
Make-up policy works through three channels represented by the three terms in the first line of Equation (29). The first term reflects the effect on inflation expectations of a commitment to make up for an error. Rational forward-looking agents respond today to the expected make-up policy they anticipate will occur, which dampens the impact of the shock. The second term represents the effect of this commitment on output gap expectations, which affect the current output gap through the permanent income hypothesis with (1 – ) representing the marginal propensity to consume from a change in current period income. The final term represents the effect of commitment on nominal interest rate expectations. Committing to offset misses shifts the expected nominal yield curve and further ameliorates the effect of any unexpected shock. The first two terms are both multiplied by , which signifies their dependence on forward-looking expectations. By contrast, the third term is multiplied by one since all agents incorporate the optimal path of interest rates into their beliefs.
The second line of Equation (29) reflects the change in the cost and benefit to make-up policy when there are learning expectations. Policy actions, like shocks, are instantiated into learning agents' beliefs when output and inflation respond and must be accounted for when implementing policy. To aid intuition, consider the case when prices are fixed, = 0. The optimal target criterion reduces to
where is
with . The central bank should set its best estimate of the output gap equal to the moving target , which is determined by the previous period's miss, . The extent to which the central bank should commit to offset past misses depends on the strength of: (i) the forward-looking income expectations channel, given by ; (ii) the nominal yield curve channel, given by the 1 in the parentheses; and (iii) the effect of learners' drifting income expectations, given by . This last term lowers the response to a given miss as g rises or falls. Make-up policy itself is a source of variation in this economy when agents are learning, which generates further drifts in beliefs that must be pre-empted.[12]
4.1.1 Mechanics of optimal policy: imperfect information
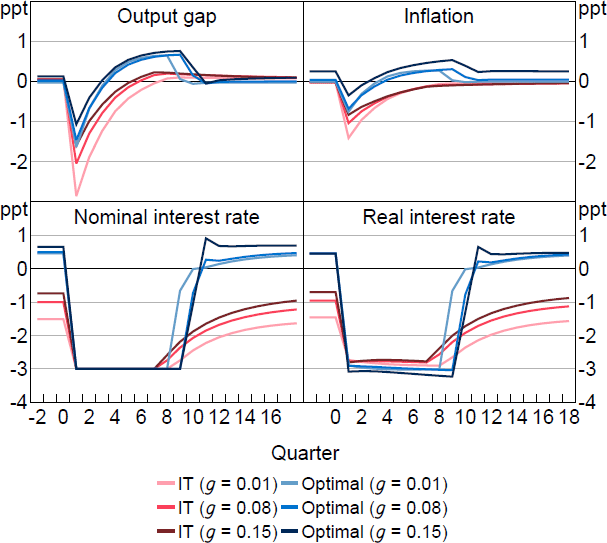
Figure 4 shows how optimal policy compares with IT in response to an unexpected cost-push shock under the same calibration explored in Figure 1. In contrast to the unconstrained case, the optimal policy is now more aggressive than IT policy. IT policy ‘lets bygones be bygones’ and does not respond to the failure to recognise the shock on impact, whereas optimal policy seeks to ‘make up’ for this miss. The anticipation of the aggressive policy acts as an automatic stabiliser when the shock occurs. Forward-looking agents understand the aggressive response is coming and that inflation will be lower in the future, which lowers inflation today. When is high, optimal policy is only a little different from the unconstrained case. This is because even under perfect information, optimal policy required only a small contemporaneous response, with a larger and persistent subsequent response. The information friction is therefore not too costly and only a small increase in make-up policy is required. When is low, the information friction makes more of a difference. With perfect information, the required contemporaneous response was large and the role of make-up policy was smaller. Imperfect information prevents the contemporaneous response, but introduces a substantial role for make-up policy because policymakers now want to influence interest rate expectations, which are forward looking even when = 0. The optimal policy prescription therefore ends up being similar across in the imperfect information case.
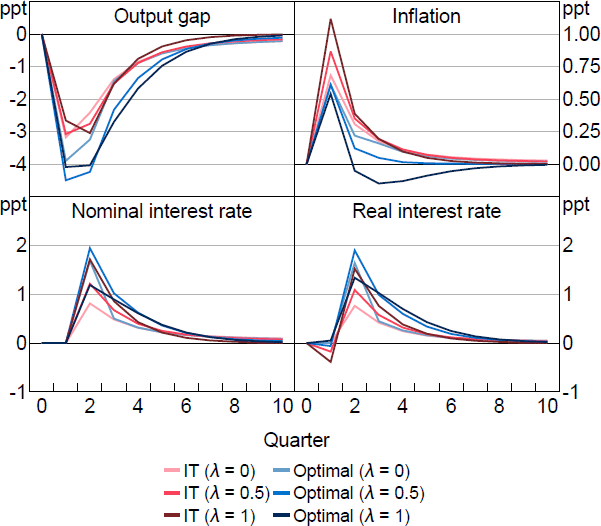
Notes: Response to a 1 per cent cost-push shock, which occurs in period 1. Parameter values are = 0.95, g = 0.08, = 0.99, = 1, = 0.1, /7.87.
Figure 5 shows the dynamics of optimal policy versus IT for an unexpected demand shock (i.e. an increase in the natural rate ). In the full information case, this shock is perfectly offset and has no effect on the output gap or inflation. Information frictions, however, change the prediction. Demand shocks generate inflation. As in the cost-push shock case, optimal policy is now more aggressive than required under IT, which causes inflation to undershoot following the shock. Once again, under imperfect information, optimal policy is similar for both high and low cases.
Notes: Response to a 1 per cent natural interest rate shock, which occurs in period 1. Parameter values are = 0.95, g = 0.08, = 0.99, = 1, = 0.1, /7.87.
4.1.2 Optimal average inflation target: imperfect information
Like the unconstrained case, a FAIT policy is robust because we can capture most of WAIT, preemption and the additional make-up policy using only a weighted average of past outcomes. In contrast to the unconstrained case, though, optimal policy requires tracking a weighted average over both inflation and the output gap.
To illustrate, we substitute into Equation (29), rearrange, and then substitute the result into Equation (28) to arrive at
where denotes the expectation conditional on . This formulation makes clear that the ‘moving target’ described in Equations (28) and (29) is equivalent to trying to set some weighted average of current and past equal to zero. Since the central bank cannot implement the full information optimal target criterion in every period, it instead tries to implement it on average over time.
As in the full information case, we can combine the optimal policy conditions with the equilibrium conditions to evaluate the expectation terms in Equation (30) (which are inside ). This gives us a description of optimal policy just in terms of past inflation and output gaps, akin to Equation (20). Assuming again that the cost-push is a first-order autoregressive process,[13] Appendix A.2 shows that, following an analogous approach to the derivation of Equation (20), we can write optimal policy under imperfect information in equilibrium as
where and are power series in L and are defined in Appendix A.2. The coefficients in the power series Qx and give the precise weight that the central bank places on current and past values of the output gap and inflation when implementing optimal policy.
Figure 6 plots these weights for different values of and g. The top row mirrors the left panel of Figure 3. It shows the case where there is no updating of learning beliefs (g = 0), which reduces the model to one featuring myopia as in Gabaix (2020). Optimal policy requires increasing weights in this case. This reflects the requirement of additional make-up policy. The bottom row of the figure shows the g 0 case. Additional make-up policy is required but it is moderated by the need to adjust for drifts in expectations. Importantly, when g is high, the optimal weights eventually decline in a similar way to the unconstrained case. It is this declining feature of the weights that makes FAIT a robust framework across a wide range of scenarios. We show in Section 5 that tracking weighted averages of inflation and output with declining weights captures most of the benefits of optimal policy.
Notes: Optimal weights on past inflation and output gap under imperfect information found in and Qx (L) in (31). Parameter values are = 0.99, = 1, = 0.1, /7.87.
4.2 Optimal policy with the zero lower bound
Optimal policy with the zero lower bound is very similar to optimal policy under imperfect information. Both constraints mean that the central bank sometimes cannot set the output gap it wants, in which case it cannot implement the full information optimal target criterion. As with imperfect information, the central bank should respond to this ZLB constraint by using commitment to influence the forward-looking expectations that enter the IS equation – that is, households' expectations over future output, inflation, and nominal interest rates. The key difference from the imperfect information case is that losses caused by a binding ZLB are not zero in expectation, even in the presence of mean zero shocks drawn from a symmetric distribution. Therefore, the pre-emptive channel of policy has a more significant role. The central bank should seek to pre-emptively raise learners' output and inflation expectations if it expects the ZLB to bind in the future. This is the use it or lose it character of optimal policy when confronted with the ZLB. It is optimal to move expectations pre-emptively before the constraint binds.
To derive optimal policy with the ZLB, we replace the information constraint (21) with the lower bound constraint
The optimal policy problem is then to choose the sequence that maximises welfare (9) subject to the constraints (10) to (13) imposed by private-sector equilibrium behaviour and the lower bound constraint (32).
The first-order conditions are the same as in the imperfect information case, except that Equation (23) is replaced with the complementary slackness condition
Just as previously represented the extent to which imperfect information constrained the central bank, it now represents the losses caused by the ZLB. It is positive when the ZLB is binding and zero otherwise.
Condition (25) is the same as before, but the expressions for and in conditions (26) and (27) take a more general form, because is no longer necessarily equal to zero for all :
If for all , then conditions (34) and (35) collapse to conditions (26) and (27). The second line of (34) indicates how the central bank can use learners' inflation expectations to lower the real interest rate when the ZLB binds. The first term in the parentheses represents the effect of raising learners' inflation expectations on the inflation expectations of the rational forward-looking agents. This term, therefore, has both pre-emptive and history-dependent aspects. The second term in the parentheses represents the effect of shifting learners' inflation expectations on future real interest rates. Similarly, (35) represents the effect of shifting learners' output expectations for future output gaps.
Conditions (25), (33), (34) and (35) define optimal policy with the ZLB constraint.
Result 5 (Optimal target criterion with ZLB). Recall that the optimal target criterion under full information and without the ZLB is , where we defined
Then the optimal target criterion when the ZLB can bind is
where and
where
is the same as Equation (29) and
Optimal policy commits to responding to past misses (see P(L)), exactly as in the information constraint case, and it adjusts the target in response to expected future target misses (P1(L–1)) and past expectations of target misses (P2(L) and P3(L–1)). The net effect is even more make-up policy is promised.
The terms P1(Z–1) and P3(L–1) capture the insurance nature of optimal policy when agents are learning. Eusepi, Gibbs and Preston (2024) coin the term the insurance principle, which says that when the duration of the ZLB is uncertain, and agents are learning, that larger front-loaded forward guidance promises are optimal. These policies are too stimulatory when the shock is short-lived, but highly effective when the shock is long-lived because of the positive contribution they make to agents' drifting beliefs. The expectations operator present in these two terms captures the idea that policy must be set according to the expectation of how long the ZLB binds, which may not match the ex post realised duration of the shock. The more learning that is present (lower ), and the faster learning happens (higher g), the more the central bank should respond now to these expectations of future binds of the ZLB.
To more clearly see how the terms in Result 5 relate to make-up and insurance policies, consider again the case where prices are fixed, . Optimal policy implies
where
with . The first line is identical to the target criterion in the imperfect information case with fixed prices. The second line represents the additional requirement of optimal policy to lift agents' expectations pre-emptively when the ZLB is expected to bind, or continue to bind. Policy should move in anticipation of a binding of the ZLB to raise expectations to pre-empt the losses that are expected to accrue while the ZLB binds.
Figure 7 compares optimal policy to IT in the presence of the ZLB.[14] First, note that even before the shock hits, optimal policy maintains a small positive output gap and inflation rate (except when g is very small). This is the pre-emptive component of optimal policy: given that the ZLB could bind with some probability in any period, it is optimal to ensure that learners' inflation and output gap expectations are somewhat above target. For larger g, shocks have greater influence over learners' expectations, and so it is optimal to ‘run the economy hotter’. Optimal policy also holds the policy rate at the ZLB for longer than IT, generating a positive output gap and inflation overshoot. This is the make-up component. As a result of these two components, the downturn when the shock hits is much smaller, even though there is some welfare loss before and after the shock. Interestingly, even though optimal policy involves a more expansionary stochastic steady state, the policy rate is higher, because inflation expectations are higher.
Notes: Response to a 1.5 per cent natural rate shock, which occurs in period 1 and has persistence 0.75. Parameter values are = 0.25, = 0.95, = 1, = 0.1, /7.87.
Figure 8 shows how the pre-emptively higher stochastic steady-state inflation target varies with , g, and the mean neutral rate, rn.[15] As expected, the inflation target is higher when g is higher, which requires more pre-emptive policy, and when rn is lower, which increases the likelihood of hitting the ZLB. When g is high, the inflation target is highest for intermediate values of , reflecting the amplification that can occur between forward-looking and backward-looking expectations through optimal pre-emptive policy.
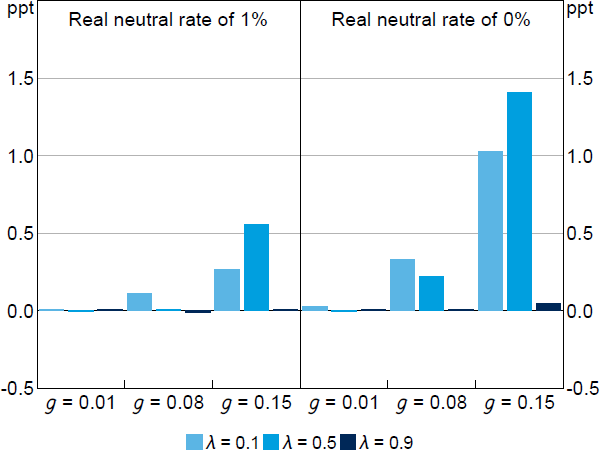
Notes: We assume that the deterministic inflation steady state is 2 per cent, so, for example, rn = 1% implies that the ZLB is 3 percentage points below steady state. The standard deviation of is 4 percentage points. Parameter values are = 0.95, = 1, = 0.1, /7.87.
5. Comparing Target Criteria
The optimal target criteria we have derived require complex considerations on the part of the central bank where policy must respond to competing objectives in precise ways. The target criteria also requires a knowledge of the underlying expectation formation process in order to implement. In this section, we ask how robust are the policy lessons we draw from the optimal criteria. In other words, how flexible can you be as a flexible average inflation targeter?
To answer this questions, we first look at how closely simple weighted-average inflation targeting schemes can perform relative to the optimal target criteria, and how do these perform against known target criteria like inflation or price-level targeting. Second, we study how these simplified optimal target criteria perform when a central bank does not know how expectations are formed and must calibrate their target criterion to maximise the average welfare for a range of different belief formation processes.
We allow for cost-push shocks and imperfect central bank information in this analysis so the policy cannot perfectly offset all demand and productivity shocks. We consider this to be the most general and realistic case.[16] Appendices D.1 and D.2 provide results for the unconstrained case, where cost-push shocks are the only source of losses.[17]
5.1 Approximating optimal policy with simple target criteria
Table 2 presents a list of simple target criteria that capture key features of the optimal target criteria in the unconstrained and constrained cases, as well as other target criteria commonly studied in the literature. The list includes inflation targeting, price-level targeting, and simple average inflation targeting rules (‘k-yr AIT’). Informed by the analytical results in the previous sections, we also include rules that incorporate some combination of an IT or weighted AIT component (‘WAIT’); a weighted average output-gap targeting component (‘WAXT’); and a preemptive component that is a forward-looking weighted average of inflation forecasts (‘preemptive’).
| Rule | Form | Parameters |
|---|---|---|
| IT | ||
| PLT | ||
| k-yr AIT | ||
| WAIT | ||
| WAIT + WAXT | ||
| IT + pre-emptive | ||
| WAIT + pre-emptive | ||
| WAIT + WAXT + pre-emptive | ||
| Note: The parameters are optimised to minimise welfare loss when implementing each rule. | ||
For each of the target criteria listed in Table 2, we find the optimal parameters that minimise welfare loss and compare it to the loss achieved under the fully optimal target criteria. For the calibration, we set = 1 and = 0.1 (equivalent to a Calvo stickiness probability of around 0.7). For the expectation formation parameters, we use a baseline of = 0.5, g = 0.08 and = 0.95. Finally, we set the persistence of the shocks to = 0.5 with the standard deviation of the neutral rate shock at ten times the standard deviation of the cost-push shock (similar to Giannoni (2014)). For simplicity, we let , so that the loss function is , with /7.87.
Table 3 presents the results. The gains from optimal policy relative to IT are large, at 36.5 per cent of the loss under IT. These gains can be almost entirely achieved by following a rule that responds to a weighted average of both past inflation and past output gaps (the ‘WAIT + WAXT’ rule). Significant gains come from making up for past output gaps, because imperfect information prevents the central bank from perfectly controlling the output gap. Recall that lagged output gap terms enter the optimal target criterion under imperfect information, Equation (28) (as with the ZLB), unlike the unconstrained case, Equation (17). The decay parameters in the WAIT and WAXT are 0.94 and 0.89, so substantial weight is placed on inflation and output outcomes in the past. The PLT rule outperforms IT. Simple AIT rules with short windows perform worse than the weighted average rules.
| Rule | Loss (% relative to IT) | |||||
|---|---|---|---|---|---|---|
| 5-yr AIT | 24.6 | 27.4 | ||||
| IT | 0 | 20.9 | ||||
| 2-yr AIT | −4.5 | 27.9 | ||||
| IT + pre-emptive | −14.8 | 0.0 | 1.60 | 1.75 | ||
| 1-yr AIT | −15.7 | 15.6 | ||||
| PLT | −23.8 | 20.3 | 1 | |||
| WAIT | −25.1 | 17.4 | 0.75 | |||
| WAIT + pre-emptive | −25.1 | 17.4 | 0.75 | 0.00 | undef | |
| WAIT + WAXT | −35.4 | 12.3 | 0.94 | 0.89 | ||
| WAIT + WAXT + pre-emptive | −35.4 | 12.3 | 0.94 | 0.89 | 0.00 | undef |
| Optimal | −36.5 | |||||
| Notes: Welfare losses are normalised relative to the welfare under IT. The parameters for each rule are optimised to minimise welfare. The optimal value of a parameter is undefined (labelled undef) if the parameter has no effect on loss at the optimum. | ||||||
The results support the idea that the average in FAIT should be a weighted average. Importantly, though, the simple target criteria all require a strong response to current inflation, which is seen by the optimised values of and . Simple AIT rules require large values as well to compensate for the 1/k weight applied to current inflation. However, it is not enough to offset the wrong type of average.
5.2 Robust optimal policy under parameter uncertainty
The previous results show that simpler targeting rules can approximate the optimal target criteria. However, the simple targeting rules require the policymaker to know , g and . Here we study what happens when the policymaker does not know these values and instead must choose a target criterion that is optimised to maximise welfare on average when , g and can take on any value in economically meaningful ranges, which we approximate with a grid. In particular, we consider the values: {0,0.25,0.5,0.75,1}, g {0,0.01,0.08,0.25,1} and p {0.95,0.99}.[18]
Table 4 shows the average welfare and the optimised parameter values for each target criterion. In addition, we show the average loss that would be achieved if the optimal criterion was implemented at each point of the grid, which represent the minimum loss achievable. WAIT rules perform best, with decay parameters of around 0.75 to 0.87. Making up for past output gaps as well via a WAXT component substantially lowers the loss. The PLT rule significantly outperforms IT. The 5-yr and 2-yr AIT rules always perform poorly.
| Rule | Average loss (% relative to IT) | |||||
|---|---|---|---|---|---|---|
| 5-yr AIT | 118.0 | 1.4 | ||||
| 2-yr AIT | 19.8 | 9.2 | ||||
| IT | 0 | 20.9 | ||||
| IT + pre-emptive | −1.3 | 14.9 | 13.0 | 1.52 | ||
| 1-yr AIT | −16.6 | 20.7 | ||||
| PLT | −22.4 | 16.8 | 1 | |||
| WAIT | −24.0 | 15.1 | 0.75 | |||
| WAIT + pre-emptive | −24.0 | 15.1 | 0.75 | 0.0 | undef | |
| WAIT + WAXT | −31.0 | 14.5 | 0.87 | 0.69 | ||
| WAIT + WAXT + pre-emptive | −31.1 | 13.3 | 0.87 | 0.66 | 6.8 | 0.00 |
| Optimal | −35.7 | |||||
| Notes: The parameters reported are set to maximise the average loss across all points in the grid. Average welfare losses are normalised relative to the welfare under IT. The optimal value of a parameter is undefined (labelled undef) if the parameter has no effect on loss at the optimum. | ||||||
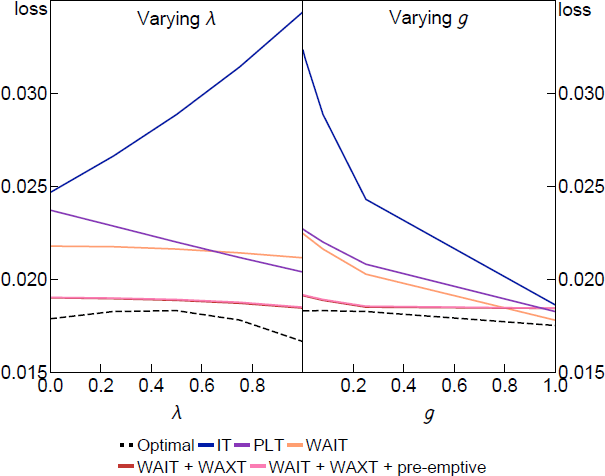
To show what lies behind the average losses in the table, Figure 9 plots the loss under a selection of target criteria from Table 4 for different values of the expectation formation parameters and g. The parameters in the policy rules are held fixed at the robustly optimal values set to minimise average loss and not optimised for each and g shown in the figure. The dashed line shows the optimal target criteria optimised at each point to show how close the simple rules with the average coefficients can come to the fully optimal policy.
The results in Figure 9 reflect the nesting of different expectations assumptions within our approach. The IT rule and PLT rules perform similarly when is low (when make-up commitments have little effect on inflation or output gap expectations) or g is high (when the sensitivity of learners' beliefs increases the cost of make-up commitments relative to their benefit).[19] When is high, make-up commitments are more powerful and the IT rule performs poorly.
In contrast, the WAIT rules generally perform well for all and g, and including a WAXT component consistently lowers the loss for all parameters (except for g = 1, when it has little effect). It is important to reiterate that this is the case even though we have fixed the coefficients of the simple WAIT and WAXT rules to their robustly optimal values in Table 4 so it is a fair comparison with the IT and PLT rules. Only in the optimal policy benchmark do we allow the policy rule parameters to change as we vary and g. The performance of the fixed-coefficient simple WAIT and WAXT rules is still remarkably close to the optimal benchmark, which illustrates the robustness of this form of FAIT.
Notes: The parameters in the policy rules are fixed at the robustly optimal values presented in Table 4. For the other parameters (other than the one changing), we set = 0.5, g = 0.08, = 0.95, = 0.1, = 1, = 0.5, = 1 and = 0.1.
5.3 Discussion
The reason that simple FAIT target criteria are robust is that once and g are in the interior of their theoretical ranges, and expectations are both backward looking and forward looking, the features of optimal policy are the same. Optimal policy requires a weighted-average inflation target and some flexible component that captures pre-emption and make up. Pre-emption appears to be satisfied in most cases simply by placing high weight on current inflation and output realisations as found in the optimised and coefficients in the WAIT + WAXT rules, while additional make-up policy is captured by including the WAXT term.[20]
6. Conclusion
It is widely recognised that rational expectations is a strong assumption and many researchers and policymakers have worried that policy recommendations that rely on it may not be robust. A large literature has shown that this concern is warranted in a variety of settings. We show that, in a framework encompassing a broad set of theories of expectation formation, flexible average inflation targeting is a robust policy strategy. Whether the central bank is unconstrained, faces information constraints or the ZLB, it is optimal to target a weighted average of inflation.
In addition, the optimal target criteria we derive give clear guidance on when policy should be flexible and deviate from the policy implied by the weighted average of inflation alone. If expectations drift in ways that are inconsistent with policymakers' objectives, then pre-emptive actions should be taken, with more agressive policy now to re-anchor beliefs. If targets are missed today, then policy should do more to make up for the misses in the future. If targets are expected to be missed in the future because of the constraint of the ZLB, then policy should do more today to insure itself against the possibility of a prolonged period of constrained actions. This guidance summarises what the flexible in FAIT should mean.
Appendix A: Derivations
A.1 Unconstrained optimal policy
The unconstrained optimal policy problem is to maximise (9) subject to (10) to (13). The first-order conditions for this problem are
From (A5), we have = 0. This is Result 1. When policy is unconstrained, the IS curve is not a binding constraint. The central bank can generate whatever output gap it wants.
Substituting = 0 into (A4) gives = 0. Learners' output gap expectations enter only the IS curve. Therefore, when policy is unconstrained, there is no reason for the central bank to try to influence learners' output gap expectations.[21]
Combining (A1) and (A2) to eliminate gives Equation (14) in the main text. Similarly, using (A1) to eliminate in (A3) gives Equation (15). The remainder of the derivation for unconstrained optimal target criterion (17) is in the main text.
A.1.1 Derivation of Equation (19)
First, we rewrite in terms of expected output gaps by substituting (14) into the second right-hand side term in (15) and iterating forward to get
Then, inverting the optimal target criterion (17) gives
The equilibrium system of (10), (12) and (A6) has the following minimum state variable solution
for some constants and au, where the second equality uses the law of motion of .
A.2 Constrained optimal policy
Suppose we add to (10) to (13) some constraint on the policy rate. This could be an information constraint (21), or a ZLB constraint (32). For this optimal policy problem, the first four first-order conditions, (A1) to (A4), remain the same. But instead of (A5), we have (22), reproduced here:
where is the Lagrange multiplier on the policy rate constraint.[22]
Using (A1) to eliminate from (A2) to (A4) and then substituting in from (22) gives (25), (34) and (35), which we reproduce here:
Now substitute (34) and (35) into (25) and collect all the non- terms in , which is defined in Result 4 in the main text. This gives
where and P(L) are defined in Result 4 and P1(L–1), P2(L) and P3(L–1) are defined in Result 5. Finally, define
So we have
To get the optimal target criterion under imperfect information, Result 4, take the expectation of (A7) with respect to the central bank's information set. Since is just a multiple of , (23) implies = 0 and = 0 for any .
To get the optimal target criterion with the ZLB, Result 5, just recognise that is non-zero if and only if the ZLB is binding.
A.2.1 Derivation of Equation (31)
Start the optimal policy conditions (25), (26) and (27). Together with the Phillips curve (10) and the updating rule for learners' inflation expectations (12), these five equations determine the optimal equilibrium paths of in terms of the paths of and the cost-push shock ut.
As in the derivation of Equation (19), we can rewrite in (26) in terms of expected output gaps instead of expected inflation:
Then combining (27) and (A8) and using the minimum state variable solution to evaluate expectations terms, we can write
where ax, and au are the same constants as in (18), and and are new constants. Combining with the updating rule for learners' inflation expectations and using (21) gives the following description of optimal policy
Or, simply , where and Qu(L) are power series in L. The new parameters are
The first and third power series, Qx(L) and Qu(L), are two different weighted averages of two exponentially weighted averages of lags. The second power series, , is a weighted average of these same two exponentially weighted averages of lags, plus a third exponentially weighted average of lags, that is,
where and are the roots of and and
Appendix B: Further Results
B.1 Optimal policy with non-rational interest rate expectations
B.1.1 When does learning about interest rates constrain policy?
To get a sense of how learning about it might alter our results, here we repeat the simple example in Section 2 of Eusepi, Giannoni and Preston (2024) with our hybrid model for expectations. Consider the model
with
Now suppose that nominal interest rate expectations are partially rational and partially learned:
For simplicity, assume all output gap and inflation expectations are fixed at steady state (the mechanism we are interested in here is the feedback between interest rates and interest rate expectations). Substituting in expectations, the interest rate path needed to implement
Substituting in
A bounded path for it and
If we substitute in
Effect of
Therefore, the first effect outweighs the second, and so increasing the share of rational agents eases the constraint.
Effect of
B.1.2 Optimal policy with learning about interest rates
For a simple example, assume prices are fixed, and continue with the assumption that output gap expectations are fixed. The optimal policy problem is
Let
The intuition in the main text around history dependence and pre-emption depending on the proportion of rational agents and learners extends to the case of interest rate expectations.
The characteristic polynomial for (B3) is very closely related to the characteristic polynomial for (B1). Condition (B2) turns out to be important for implementing this optimal target criterion:[24]
- If (B2) is satisfied, then the target criterion (B3) pins down a unique path for xt (which converges to xt = 0). Substituting it into the IS curve gives a non-explosive path for it.
- If (B2) is not satisfied, then there are infinitely many paths for xt that satisfy the target criterion. But, substituting into the IS curve, only one of those paths implies a bounded path for it and
ω t i
If
B.2 Optimal policy under discretion
What would our optimal targeting rules look like under discretion? This is a difficult question to address analytically in our full model, but we can consider a two-period version of our model to get some intuition:
B.2.1 Optimal policy under commitment
We start by solving for optimal commitment policy in this two-period model so that we have a benchmark to which we can compare optimal discretionary policy. The first-order conditions under commitment are
Eliminating the multipliers gives the optimal target criteria:
The heterogeneity of expectations and the interaction between rational and learners' expectations is important (i.e. the denominators increase to 1 if
B.2.2 Optimal policy under discretion
Working backwards, optimal policy under discretion in the second period is
Then in the first period, the policymaker faces the constraints (B4), (B5) and (B8). The first-order conditions are
Eliminating the multipliers gives the optimal target criterion
Compare (B9) to the optimal commitment policy (B6). Optimal policy under discretion places less weight on both inflation terms. Again heterogeneity is important: this difference is only because of the interaction between rational agents and learners. If
The reason why discretion involves less response to inflation is because the future policymaker will not be responding to past inflation. So there is no need to use learners' expectations to ease the cost of doing so. With both learning and rational expectations, there is still some reason to lift learners' inflation expectations, because that will affect future inflation and thereby influence current rational inflation expectations. But the future policymaker will attempt to offset this inflation rather than accomodate it, so the effect is less powerful.
Appendix C: Optimal Policy with Infinite-horizon Phillips Curve
C.1 Infinite-horizon Phillips curve
In the main text, we model firms' pricing decisions by taking the standard New Keynesian Phillips curve and substituting our alternative specification for aggregate inflation expectations into the expectation term. This is consistent with the ‘Euler equation’ approach to adaptive learning, and also approximates a range of other behavioural theories. But it is not consistent with the ‘anticipated utility’ approach to adaptive learning. In this appendix, we provide optimal policy results using an ‘anticipated utility’ specification for the Phillips curve:
Here the parameter
Using our specification for agents' beliefs, (3) to (6), we have
The optimal policy problem is the same as in the main text, but with a different Phillips curve, that is, choose the sequence
The first-order conditions are
plus an additional condition for
C.2 Unconstrained case
In the absence of imperfect central bank information or the ZLB, the additional first-order condition is
The multipliers
Solving forward for
where
Using this solution to substitute for
This optimal target criterion has the same structure as the analogous one in the main body, (17). It includes a make-up component and a pre-emptive component, and the intuition behind it is the same. The differences are a matter of degree. First, the optimal weights on past outcomes decay more slowly in (C4). This is because the infinite-horizon Phillips curve implies that make-up commitments further into the future have a stronger effect on current-period pricing decisions than is the case with the one-step-ahead Phillips curve.[26] Second, the optimal pre-emptive response to expected future inflation is stronger. This is because policy-induced changes in learners' beliefs now have a stronger effect on future outcomes, because both their inflation and output gap expectations influence their pricing decisions (with the one-step-ahead Phillips curve, only their inflation expectations were relevant).
Table C1 compares the performance of the simple target criteria from Table 2 under the infinite-horizon Phillips curve. The equivalent values for the one-step-ahead Phillips curve (i.e. Table D1) are in parentheses. The results are fairly similar. As the previous paragraph would suggest, the main differences are that with the infinite-horizon Phillips curve (i) the optimal weight
| Rule | Loss (% relative to IT) | |||||
|---|---|---|---|---|---|---|
| 5-yr AIT | 61.1 (96.5) | 16.9 (31.3) | ||||
| 2-yr AIT | 16.8 (48.8) | 18.5 (13.0) | ||||
| 1-yr AIT | 2.8 (7.7) | 15.0 (21.5) | ||||
| IT | 0 (0) | 10.6 (11.6) | ||||
| IT + pre-emptive | −0.0 (−4.4) | 10.6 (0.03) | 0.00 (1.09) | undef (1.50) | ||
| PLT | −5.9 (6.6) | 6.6 (9.1) | 1 (1) | |||
| WAIT | −11.0 (−6.6) | 6.9 (8.4) | 0.70 (0.52) | |||
| WAIT + pre-emptive | −12.5 (−6.6) | 5.5 (8.2) | 0.89 (0.52) | 10.92 (0.33) | 0.00 (1.02) | |
| WAIT + WAXT | −12.5 (−6.6) | 8.0 (8.4) | 0.88 (0.53) | 0.43 (0.01) | ||
| WAIT + WAXT + pre-emptive | −12.5 (−6.6) | 7.9 (8.2) | 0.88 (0.52) | 0.43 (0.00) | 0.12 (0.33) | 0.03 (1.02) |
| Optimal | −12.5 (−6.6) | |||||
| Notes: Welfare losses are normalised relative to the welfare under IT. The parameters for each rule are optimised to minimise welfare. The optimal value of a parameter is undefined (labelled undef) if the parameter has no effect on loss at the optimum. Values in parentheses are the equivalent values with the one-step-ahead Phillips curve (from Table D1). | ||||||
C.3 Comparison to Eusepi, Giannoni and Preston (2018)
Eusepi et al (2018) study optimal policy in an adaptive learning model (without imperfect information or the ZLB). They show that in this setting, the infinite-horizon Phillips curve under some calibrations implies that optimal policy is history dependent, whereas it is not history dependent under the one-step-ahead Phillips curve.
If we set
Setting
The difference in the optimal equilibrium stems not from the optimal policy rules, but from the direct effect of beliefs on the Phillips curve. Only inflation beliefs enter the one-step-ahead Phillips curve, so the Phillips curve will always shift up following an inflationary cost-push shock, then return to its original position. In contrast, both inflation and output gap beliefs enter the infinite-horizon Phillips curve. If the loss function places sufficiently low weight on the output gap term, then the central bank's aggressive response will cause the Phillips curve to shift downwards (once the initial shock has dissipated), which means that inflation will overshoot. It is the private sector pricing decisions that are history dependent (via beliefs) and overshoot, not the policy rule.
C.4 General case
If there is a constraint on the policy rate (e.g. due to imperfect central bank information or the ZLB), then
The multipliers on learners' beliefs are
Solving forward for
Using this solution to substitute for
where
Now define
so we have
The optimal target criterion is then the same as with the one-step-ahead Phillips curve in Result 5, with the newly defined
As in the unconstrained case, the main differences between this optimal target criterion and the one with the one-step-ahead Phillips curve are that (i) the weight on lagged misses is larger, because commitments further in the future have a larger effect on current-period inflation via the Phillips curve, and (ii) the optimal pre-emptive response to expected future misses is larger, because the central bank has greater effect on future outcomes now that learners' beliefs about both inflation and the output gap affect inflation.
Since both the make-up and pre-emptive channels of policy are stronger, the interaction between them is also strengthened. But this interaction has offsetting effects, so the change in optimal policy is small.[27]
Table C2 compares the performance of the simple target criteria from Table 2 under the infinite-horizon Phillips curve with imperfect central bank information. The equivalent values for the one-step-ahead Phillips curve (i.e. Table 3) are in parentheses. The results are very similar.
| Rule | Loss (% relative to IT) | |||||
|---|---|---|---|---|---|---|
| 5-yr AIT | 18.2 (24.6) | 23.8 (27.4) | ||||
| IT | 0 (0) | 20.9 (20.9) | ||||
| IT + preemptive | −2.3 (−14.8) | 27.1 (0.0) | 10.04 (1.60) | 1.28 (1.75) | ||
| 2-yr AIT | −5.9 (−4.5) | 34.3 (27.9) | ||||
| 1-yr AIT | −12.3 (−15.7) | 24.4 (15.6) | ||||
| PLT | −18.8 (−23.8) | 9.2 (20.3) | 1 (1) | |||
| WAIT | −20.0 (−25.1) | 9.6 (17.4) | 0.80 (0.75) | |||
| WAIT + pre-emptive | −20.0 (−25.1) | 9.6 (17.4) | 0.80 (0.75) | 0.00 (0.00) | undef (undef) | |
| WAIT + WAXT | −29.5 (−35.4) | 10.0 (12.3) | 0.97 (0.94) | 0.69 (0.89) | ||
| WAIT + WAXT + pre-emptive | −29.5 (−35.4) | 10.0 (12.3) | 0.97 (0.94) | 0.69 (0.89) | 0.00 (0.00) | undef(undef) |
| Optimal | −30.5 (−36.5) | |||||
| Notes: Welfare losses are normalised relative to the welfare under IT. The parameters for each rule are optimised to minimise welfare. The optimal value of a parameter is undefined (labelled undef) if the parameter has no effect on loss at the optimum. Values in parentheses are the equivalent values with the one-step-ahead Phillips curve (from Table 3). | ||||||
C.5 Robustly optimal policy under parameter uncertainty with the infinite-horizon Phillips curve
Tables C3 and C4 replicate the robustly optimal policy exercise in Tables D2 and 4, but with the infinite-horizon Phillips curve. The results are very similar.
| Rule | Average loss (% relative to IT) | |||||
|---|---|---|---|---|---|---|
| 5-yr AIT | 5.6 × 1011 (535.6) | 1.0 (1.2) | ||||
| 2-yr AIT | 187.8 (136.1) | 1.1 (7.4) | ||||
| 1-yr AIT | 86.3 (9.7) | 2.6 (19.9) | ||||
| PLT | 0.5 (4.2) | 8.0 (10.9) | 1 (1) | |||
| IT | 0 (0) | 6.2 (13.7) | ||||
| IT + pre-emptive | −9.9 (−0.4) | 6.4 (3.0) | 10.37 (14.9) | 0.00 (0.42) | ||
| WAIT | −14.6 (−8.1) | 7.0 (9.2) | 0.53 (0.56) | |||
| WAIT + WAXT | −15.4 (−8.1) | 6.9 (9.4) | 0.73 (0.60) | 0.29 (0.08) | ||
| WAIT + pre-emptive | −16.5 (−8.9) | 5.5 (7.2) | 0.74 (0.67) | 11.60 (7.4) | 0.00 (0.51) | |
| WAIT + WAXT + pre-emptive | −16.6 (−8.9) | 6.6 (7.2) | 0.73 (0.67) | 0.17 (0.00) | 6.91 (7.4) | 0.00 (0.51) |
| Optimal | −21.2 (−13.7) | |||||
| Notes: The parameters reports are set to maximise the average loss across all points in the grid. Average welfare losses are normalised relative to the welfare under IT. Values in parentheses are the equivalent values with the one-step-ahead Phillips curve (from Table D2). | ||||||
| Rule | Average loss (% relative to IT) | |||||
|---|---|---|---|---|---|---|
| 5-yr AIT | 2.3 ×1011 (118.0) | 1.0 (1.4) | ||||
| 2-yr AIT | 58.9 (19.8) | 0.8 (9.2) | ||||
| 1-yr AIT | 27.0 (−16.6) | 2.0 (20.7) | ||||
| IT | 0 (0) | 4.8 (20.9) | ||||
| PLT | −16.8 (−22.4) | 7.4 (16.8) | 1 (1) | |||
| IT + pre-emptive | −17.3 (−1.3) | 6.7 (14.9) | 16.92 (13.0) | 1.67 (1.52) | ||
| WAIT | −22.7 (−24.0) | 6.1 (15.1) | 0.66 (0.75) | |||
| WAIT + WAXT | −26.9 (−31.0) | 4.7 (14.5) | 0.83 (0.87) | 0.28 (0.69) | ||
| WAIT + pre-emptive | −27.0 (−24.0) | 12.1 (15.1) | 0.65 (0.75) | 14.53 (0.0) | 0.00 (undef) | |
| WAIT + WAXT + pre-emptive | −33.5 (−31.1) | 8.9 (13.3) | 0.86 (0.87) | 0.51 (0.66) | 14.54 (6.8) | 0.28 (0.00) |
| Optimal | −38.2 (−35.7) | |||||
| Notes: The parameters reports are set to maximise the average loss across all points in the grid. Average welfare losses are normalised relative to the welfare under IT. The optimal value of a parameter is undefined (labelled undef) if the parameter has no effect on loss at the optimum. Values in parentheses are the equivalent values with the one-step-ahead Phillips curve (from Table 4). | ||||||
Appendix D: Robustly Optimal Policy in the Unconstrained Case
This appendix replicates the numerical results in Section 5 for the unconstrained case, where the central bank has perfect control of the output gap (i.e. perfect information and no ZLB).
D.1 Simple target criteria in the unconstrained case
Table D1 presents the optimal simple target criteria (defined in Table 2) under the baseline calibration. Optimal policy reduces the loss by 6.6 per cent compared to the loss under the IT rules. These gains can be almost entirely achieved by following a WAIT rule with a decay parameter of 0.52 (close to the share of rational agents,
| Rule | Loss (% relative to IT) | |||||
|---|---|---|---|---|---|---|
| 5-yr AIT | 96.5 | 31.3 | ||||
| 2-yr AIT | 48.8 | 13.0 | ||||
| 1-yr AIT | 7.7 | 21.5 | ||||
| PLT | 6.6 | 9.1 | 1 | |||
| IT | 0 | 11.6 | ||||
| IT + pre-emptive | –4.4 | 0.03 | 1.09 | 1.50 | ||
| WAIT | –6.6 | 8.4 | 0.52 | |||
| WAIT + WAXT | –6.6 | 8.4 | 0.53 | 0.01 | ||
| WAIT + pre-emptive | –6.6 | 8.2 | 0.52 | 0.33 | 1.02 | |
| WAIT + WAXT + pre-emptive | –6.6 | 8.2 | 0.52 | 0.00 | 0.33 | 1.02 |
| Optimal | –6.6 | |||||
| Notes: Welfare losses are normalised relative to the welfare under IT. The parameters for each rule are optimised to minimise welfare. | ||||||
D.2 Optimal policy under parameter uncertainty in the unconstrained case
Table D2 shows the average welfare and optimised parameter values for each target criterion when the policymaker is uncertain about expectations formation (i.e. across a set of different
Note that under the infinite-horizon Phillips curve, the optimal make-up weights in the unconstrained case are a bit larger (see Appendix C.2), so optimal policy in the unconstrained case is not as different from the constrained case.
| Rule | Average loss (% relative to IT) | |||||
|---|---|---|---|---|---|---|
| 5-yr AIT | 535.6 | 1.2 | ||||
| 2-yr AIT | 136.1 | 7.4 | ||||
| 1-yr AIT | 9.7 | 19.9 | ||||
| PLT | 4.2 | 10.9 | 1 | |||
| IT | 0 | 13.7 | ||||
| IT + pre-emptive | –0.4 | 3.0 | 14.9 | 0.42 | ||
| WAIT | –8.1 | 9.2 | 0.56 | |||
| WAIT + WAXT | –8.1 | 9.4 | 0.60 | 0.08 | ||
| WAIT + pre-emptive | –8.9 | 7.2 | 0.67 | 7.4 | 0.51 | |
| WAIT + WAXT + pre-emptive | –8.9 | 7.2 | 0.67 | 0.00 | 7.4 | 0.51 |
| Optimal | –13.7 | |||||
| Notes: The parameters reports are set to maximise the average loss across all points in the grid. Average welfare losses are normalised relative to the welfare under IT. | ||||||
To show what lies behind the average losses in the table, Figure D1 plots the loss under a selection of target criteria from Table D2 for different values of the expectation formation parameters
The IT rule performs well when
As in the constrained case, the WAIT rules perform consistently well across all parameter values. This is the case even though we have fixed the weight in the WAIT rules to the robustly optimal values in Table D2 so it is a fair comparison with the IT and PLT rules. Only in the optimal policy benchmark do we allow the policy rule parameters to change as we vary
Notes:
The parameters in the policy rules are fixed at the robustly optimal values presented in Table D2. For the other parameters (other than the one changing), we set
References
Angeletos G-M and Z Huo (2021), ‘Myopia and Anchoring’, The American Economic Review, 111(4), pp 1166–1200.
Angeletos G-M, Z Huo and KA Sastry (2021), ‘Imperfect Macroeconomic Expectations: Evidence and Theory’, in M Eichenbaum and E Hurst (eds), NBER Macroeconomics Annual, 35, University of Chicago Press, Chicago, pp 1–86.
Angeletos G-M and C Lian (2018), ‘Forward Guidance without Common Knowledge’, The American Economic Review, 108(9), pp 2477–2512.
Arias J, M Bodenstein, H Chung, T Drautzburg and A Raffo (2020), ‘Alternative Strategies: How Do They Work? How Might They Help?’, Board of Governors of the Federal Reserve System Finance and Economics Discussion Series No 2020-068.
Benchimol J and L Bounader (2023), ‘Optimal Monetary Policy under Bounded Rationality’, Journal of Financial Stability, 67, Article 101151.
Bernanke BS, MT Kiley and JM Roberts (2019), ‘Monetary Policy Strategies for a Low-rate Environment’, in WR Johnson and K Markel (eds), AEA Papers and Proceedings, 109, American Economic Association, Nashville, pp 421–426.
Branch WA and B McGough (2009), ‘A New Keynesian Model with Heterogeneous Expectations’, Journal of Economic Dynamics & Control, 33(5), pp 1036–1051.
Brock WA and CH Hommes (1997), ‘A Rational Route to Randomness’, Econometrica, 65(5), pp 1059–1095.
Budianto F, T Nakata and S Schmidt (2023), ‘Average Inflation Targeting and the Interest Rate Lower Bound’, European Economic Review, 152, Article 104384.
Clarida R, J Galí and M Gertler (1999), ‘The Science of Monetary Policy: A New Keynesian Perspective’, Journal of Economic Literature, 37(4), pp 1661–1707.
Cole SJ and E Martínez-García (2023), ‘The Effect of Central Bank Credibility on Forward Guidance in an Estimated New Keynesian Model’, Macroeconomic Dynamics, 27(2), pp 532–570.
Di Bartolomeo G, M Di Pietro and B Giannini (2016), ‘Optimal Monetary Policy in a New Keynesian Model with Heterogeneous Expectations’, Journal of Economic Dynamics & Control, 73, pp 373–387.
Dorich J, RR Mendes and Y Zhang (2021), ‘The Bank of Canada's “Horse Race” of Alternative Monetary Policy Frameworks: Some Interim Results from Model Simulations’, Bank of Canada Staff Discussion Paper 2021-13.
Duineveld S (2021), ‘Standardized Projection Algorithms to Solve Dynamic Economic Models’, Unpublished manuscript, 3 December.
Dupraz S, H Le Bihan and J Matheron (2024), ‘Make-up Strategies with Finite Planning Horizons but Infinitely Forward-looking Asset Prices’, Journal of Monetary Economics, 143, Article 103542.
Dupraz S and M Marx (2023), ‘Anchoring Boundedly Rational Expectations’, Banque de France Working Paper No 936.
Eggertsson GB and M Woodford (2003), ‘Optimal Monetary Policy in a Liquidity Trap’, NBER Working Paper No 9968.
Eo Y and D Lie (2020), ‘Average Inflation Targeting and Interest-rate Smoothing’, Economics Letters, 189, Article 109005.
Eskelinen M, CG Gibbs and N McClung (2024), ‘Resolving New Keynesian Puzzles’, Bank of Finland Research Discussion Papers 5/2024.
Eusepi S, MP Giannoni and B Preston (2018), ‘Some Implications of Learning for Price Stability’, European Economic Review, 106, pp 1–20.
Eusepi S, MP Giannoni and B Preston (2024), ‘The Short-run Policy Constraints of Long-run Expectations’, Unpublished manuscript, 10 April.
Eusepi S, CG Gibbs and B Preston (2024), ‘Monetary Policy as Insurance’, Paper presented at RBA Quantitative Macroeconomics Research Workshop, Sydney, 19–20 December.
Eusepi S and B Preston (2018), ‘The Science of Monetary Policy: An Imperfect Knowledge Perspective’, Journal of Economic Literature, 56(1), pp 3–59.
Evans GW, CG Gibbs and B McGough (forthcoming), ‘A Unified Model of Learning to Forecast’, American Economic Journal: Macroeonomics.
Evans GW and S Honkapohja (2001), Learning and Expectations in Macroeconomics, Frontiers of Economic Research, Princeton University Press, Princeton.
Evans GW and S Honkapohja (2003), ‘Expectations and the Stability Problem for Optimal Monetary Policies’, The Review of Economic Studies, 70(4), pp 807–824.
Evans GW and B McGough (2010), ‘Implementing Optimal Monetary Policy in New-Keynesian Models with Inertia’, The B.E. Journal of Macroeconomics, 10(1), Topics, Article 5.
Farhi E and I Werning (2019), ‘Monetary Policy, Bounded Rationality, and Incomplete Markets’, The American Economic Review, 109(11), pp 3887–3928.
Gabaix X (2020), ‘A Behavioral New Keynesian Model’, The American Economic Review, 110(8), pp 2271–2327.
Gasteiger E (2014), ‘Heterogeneous Expectations, Optimal Monetary Policy, and the Merit of Policy Inertia’, Journal of Money, Credit and Banking, 46(7), pp 1535–1554.
Gasteiger E (2021), ‘Optimal Constrained Interest-rate Rules under Heterogeneous Expectations’, Journal of Economic Behavior & Organization, 190, pp 287–325.
Giannoni MP (2014), ‘Optimal Interest-rate Rules and Inflation Stabilization versus Price-level Stabilization’, Journal of Economic Dynamics & Control, 41, pp 110–129.
Giannoni MP and M Woodford (2005), ‘Optimal Inflation-targeting Rules’, in BS Bernanke and M Woodford (eds),The Inflation-targeting Debate, NBER Studies in Business Cycles, Vol 32, University of Chicago Press, Chicago, pp 93–172.
Gibbs CG (2017), ‘Forecast Combination, Non-linear Dynamics, and the Macroeconomy’, Economic Theory, 63(3), pp 653–686.
Gibbs CG and M Kulish (2017), ‘Disinflations in a Model of Imperfectly Anchored Expectations’, European Economic Review, 100, pp 157–174.
Hagenhoff T (2021), ‘Optimal Monetary Policy, Heterogeneous Expectations and Consumption Dispersion’, Unpublished manuscript, University of Bamberg, 26 April.
Hebden J, EP Herbst, J Tang, G Topa and F Winkler (2020), ‘How Robust Are Makeup Strategies to Key Alternative Assumptions?’, Board of Governors of the Federal Reserve System Financial and Economics Discussion Series 2020-069.
Honkapohja S and N McClung (2024a), ‘Average Inflation Targeting in Calvo Model with Imperfect Knowledge and Learning’, Bank of Finland Research Discussion Papers 13/2024.
Honkapohja S and N McClung (2024b), ‘On Robustness of Average Inflation Targeting’, Unpublished manuscript, 5 March.
Honkapohja S and K Mitra (2020), ‘Price Level Targeting with Evolving Credibility’, Journal of Monetary Economics, 116, pp 88–103.
Molnár K and S Santoro (2014), ‘Optimal Monetary Policy when Agents are Learning’, European Economic Review, 66, pp 39–62.
Orphanides A and JC Williams (2007), ‘Robust Monetary Policy with Imperfect Knowledge’, Journal of Monetary Economics, 54(5), pp 1406–1435.
Preston B (2005), ‘Learning about Monetary Policy Rules when Long-horizon Expectations Matter’, International Journal of Central Banking, 1(2), pp 81–126.
Preston B (2006), ‘Adaptive Learning, Forecast-based Instrument Rules and Monetary Policy’, Journal of Monetary Economics, 53(3), pp 507–535.
Svensson LEO and M Woodford (2005), ‘Implementing Optimal Policy through Inflation-forecast Targeting’, in BS Bernanke and M Woodford (eds), The Inflation-targeting Debate, NBER Studies in Business Cycles, Vol 32, University of Chicago Press, Chicago, pp 19–92.
Woodford M (2003), Interest and Prices: Foundations of a Theory of Monetary Policy, Princeton University Press, Princeton.
Woodford M (2010), ‘Optimal Monetary Stabilization Policy’, in BM Friedman and M Woodford (eds), Handbook of Monetary Economics: Volume 3B, Handbooks in Economics, Elsevier, Amsterdam, pp 723–828.
Work Stream on the Price Stability Objective (2021), ‘The ECB's Price Stability Framework: Past Experience, and Current and Future Challenges’, European Central Bank Occasional Paper Series No 269.
Acknowledgements
We thank Bruce Preston, Ippei Fujiwara, Nigel McClung, Matthew Read, and Jonathan Hambur for helpful comments and suggestions. We thank seminar participants at the Bank of Finland and the organisers of the Workshop of the Australasian Economic Society 2022, Econometric Society Australasian Meetings 2023, and the 2023 Reserve Bank of Australia's Quantitative Macroeconomics Workshop for allowing us to present. The views expressed in this paper are those of the authors and should not be attributed to the Reserve Bank of Australia. Any errors are the sole responsibility of the authors.
Footnotes
Eusepi and Preston (2018) and Eusepi, Giannoni and Preston (2018) also point to this feature of adaptive learning models relative to rational expectations models when analysing unconstrained optimal policy. We show how this insight generalises to several novel environments. [1]
There has been a gradual evolution of the language describing different characterisations of monetary policy. Svensson and Woodford define a monetary policy rule broadly as a prescribed guide for monetary policy. Target criterion and interest rate rules are two different ways of specifying a policy rule in their framework. In more recent treatments in the literature, there is no distinction made between interest rate rules and policy rules. The two are synonymous. We adopt the term ‘policy framework’ to capture the broader notion of a general policy that may be implemented with a target criterion or an interest rate rule. [2]
Di Bartolomeo, Di Pietro and Giannini (2016) and Hagenhoff (2021) also consider a heterogeneous expectations framework, but their focus is on how heterogeneity in expectations across agents affects price and consumption dispersion, altering the micro-founded loss function. We are instead interested in capturing how a broad range of different expectations models affect optimal aggregate outcomes, so we assume the standard loss function. [3]
This is especially important because we are going to make different assumptions about the formation of output gap and interest rate expectations. In the two-period ‘Euler equation’ representation, nominal interest rate expectations do not even appear. See Preston (2005) for a detailed discussion of the two representations. [4]
We focus on how forward- or backward-looking monetary policy should be to achieve optimal aggregate outcomes and do not consider distributional consequences that may occur due to heterogeneity in expectations. We maintain a representative agent assumption where the representative decision-maker takes a weighted average of forecasts from two different models: the correct structural model, and a reduced-form model which is re-estimated each period. Therefore, the representative agent assumption is maintained. This is the approach taken in Gibbs (2017) and Gibbs and Kulish (2017). [5]
Note that we still allow for drift in longer-term real interest rates due to drifting beliefs about future inflation. [6]
Farhi and Werning (2019) assume that households perfectly observe future policy rates, but deduce the consequences for inflation and output gap expectations using level-k reasoning. Similarly, Dupraz et al (2024) model households with finite-planning horizons, but who save and borrow based on financial prices determined by intermediaries with fully rational expectations over nominal interest rates. Quantitative evaluations of make-up policy by Federal Reserve Board staff have have used versions of their semi-structural model (FRB-US) in which financial market participants have model-consistent expectations, even while households and firms may not be rational (Bernanke, Kiley and Roberts 2019; Hebden et al 2020). [7]
There are clearly interesting questions about what occurs when the central bank lacks credibility over the path of interest rates that it plans to implement. See, for example, Eusepi et al (2018) and Eusepi, Giannoni and Preston (2024). Our results represent a best case scenario with respect to central bank credibility regarding the policy rate path. In Appendix B.1, we discuss how our results might be affected if policy rate expectations are not entirely rational. [8]
In Appendix B.2, we use a simple two-period model to explore what optimal policy under discretion would look like with our hybrid specification for expectation formation. [9]
That is,
For reasonable calibrations,
The private sector continues to make decisions based on the full information set, It. This means that when an unexpected shocks occurs, their expectations of future policy will adjust before the central bank moves the actual policy rate. This is what underlies the ‘automatic stabiliser’ mechanism discussed below. [11]
Eusepi, Giannoni and Preston (2024) explore this feature of learning models in depth, focusing on the transmission of short-run interest rate to long-run interest rate expectations, which is absent in our model. In Appendix B.1, we discuss how our results might be affected if some agents form policy rate expectations by learning, instead of rationally. [12]
Only the unexpected component of the IS curve shock is relevant to optimal policy. The central bank can fully offset any expected component, just as it does in the full information case. [13]
To solve the model with the ZLB, we use a policy function iteration method, drawing on code in Sijmen Duineveld's PROMES toolbox (Duineveld 2021). [14]
Here, when we say ‘steady-state inflation target’, we are referring to the stochastic steady state, meaning the value that inflation converges to in the absence of shocks, but where agents still expect that shocks could occur in the future. [15]
Alternatively, we could also allow for an occasionally-binding ZLB. However, as we show in Result 5, imperfect central bank information captures key features of the ZLB constraint, in that both prevent the central bank from perfectly controlling the output gap. The main difference is that target misses due to the ZLB are non-zero in expectation, so allowing the ZLB when optimising the simple target criteria outlined below would likely result in a stronger pre-emptive response to expected future outcomes. [16]
The main difference is that the optimal degree of make-up policy is lower when the central bank has perfect control of the output gap, as the analytical results in previous sections suggest. Compared to the imperfect information case, the optimal weight on lagged inflation and output gap outcomes is smaller, PLT underperforms IT, and IT in general is closer to optimal policy. That said, Appendix C.2 shows that allowing for an infinite-horizon Phillips curve somewhat increases the optimal degree of make-up policy in the unconstrained case, making it more like the imperfect information case. [17]
We set the other parameters at the baseline calibration described in the previous section. [18]
PLT still slightly outperforms IT even when
If we allowed for the ZLB, including an explicit pre-emption term would likely offer a greater improvement in welfare (at least if the steady-state neutral rate is sufficiently low). Increasing the persistence of the cost-push shocks might have a similar effect. [20]
This conclusion would not hold if we had an infinite-horizon Phillips curve, as in Eusepi et al (2018), because output gap expectations would then enter the Phillips curve. [21]
A similar first-order condition would apply if, instead of a constraint on the policy rate, the loss function contained a policy rate stability or smoothing term. Then
For all parameterisations, the roots of the characteristic polynomial for (B1) are real, and only one is greater than 1. A bounded path for it and
The roots of the characteristic polynomial for (B3) are the reciprocals of the roots of the characteristic polynomial for (B1) (setting
With the one-step-ahead Phillips curve, commitments about policy more than one period ahead still influence current-period outcomes via the inflation expectations of rational agents. But this effect occurs via a general equilibrium channel and is therefore dampened by the presence of non-rational agents. With the infinite-horizon Phillips curve, these commitments affect the pricing decisions of rational agents directly, via both their inflation and output gap expectations, without this dampening. [26]
The dynamic interaction between rational and learners' expectations in the Phillips curve tends to strengthen the effect of both make-up and pre-emptive policy relative to its cost (this is captured in the first term in