RDP 2023-02: Did Labour Market Concentration Lower Wages Growth Pre-COVID? 5. Wages and concentration
March 2023
- Download the Paper 1.8MB
While there is no evidence of a general increase in concentration in Australian labour markets, the relationship between concentration and wages is still relevant. Given such a relationship should exist in theory, its presence would indicate that the measure of concentration has some economic signal, and so would be worth tracking.
As noted earlier, other factors could be important in mitigating or amplifying the effect of labour market concentration on wages. As such, we might need to take account of these additional factors in considering whether labour market concentration has weighed on wages in recent years, rather than just examining aggregate concentration levels.
To provide some initial evidence on the relationship between concentration and wages, Figure 5 plots changes in the HHI index over the sample for labour markets against their average annual real wages growth. Real wages growth has tended to be higher in local labour markets where the HHI has declined, providing some initial evidence that local labour market concentration is associated with lower wages.
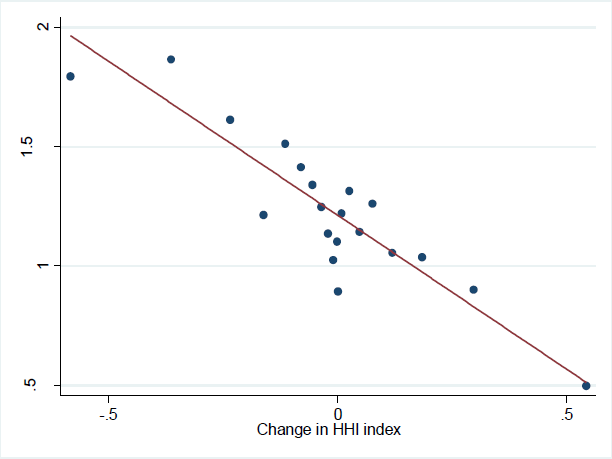
Note: Plots changes in HHI in local labour markets against the average growth in their real wages over the sample. Dots are average for buckets of firms, line is line of best fit.
Source: Author's calculations
5.1. Model specification and identification
To test this more formally, I now turn to a regression framework. In specifying the regression, it is important to think about how wages are set.
As discussed in Manning (2021), in many models of labour market power the firm optimally sets its wages some fraction below its marginal revenue product of labour (MRPL, closely linked to productivity). The extent of this markdown will be a function of the firm's market power (the elasticity of its labour supply curve ). As such, these models predict that the wage (for the market or firm) can be written as:[7]
In our case, the market power is summarised by the measure of concentration. The degree of market power could be market specific, or firm specific, depending on the model.
This set-up leads to our first two models:
- Monopsonistic competition: Wages are set as markdown on the MRPL, with this markdown being the same for all firms and being related to the market concentration. This is the standard regression framework used in most papers (Rinz 2018; Azar et al 2020).
- Oligopsony: As a simple extension, we can allow the degree of market power to vary with plant size . In this case the markdown differs based on the plant's power, which is related to its market share. This oligopsonistic framework is more in line with recent papers such as Berger et al (2021).
In each case, the coefficient of interest is .
For both models Xi,t contains several controls, including industry-by-time and location-by-time effects, and market size. These controls help us to strip out factors affecting all firms or markets, such as local or industry demand, and focus on changes in concentration that reflect changes in market power for the market or firm. Potential examples of such changes include: an exogenous change in the number of competitors (such as due to M&A); technological changes in the ease of finding jobs; and changes in workers' views of the substitutability of different employers, such as differences in cultures.
Some papers use instruments to help identify exogenous changes in market power/supply elasticity. The key concern is that some shocks can affect wages both by impacting the MRPL, as well by changing the concentration and labour supply elasticity and, therefore, markdown. If no measure of productivity is included both effects will be attributed to concentration.
This concern is lessened somewhat because I include a measure of productivity. Still, as productivity measurement is imperfect, I also estimate a version of the monopsony model where I use an instrument for concentration. Specifically, I use the average of the (inverse of the) number of plants in the industry in other locations, with each location being weighted by its share of industry employment. This approach is used in a number of papers (such as Azar et al 2020). The use of the number of firms, rather than the HHI, should lessen the impact of shocks to individual firms, while focusing on national changes allows us to abstract from local shocks. That said, this approach makes it difficult to include industry by time effects, and so is not the preferred specification.[8]
Several recent models have also argued that the degree of market concentration can affect the pass-through of firm-level productivity shocks onto wages. In oligopolistic models such as by Berger et al (2021) and Benmelech et al (2022), increases in productivity, which make the firm larger, move it onto a steeper part of the labour supply curve. As such the markdown increases, leading wages to increase by less than productivity, meaning the pass-through to wages is incomplete. Moreover, the degree of pass-through tends to decline as firms become larger, and as such pass-through becomes a function of firms' market shares. Such a specification also naturally comes out of some search-and-match based models of the labour market (Jarosch et al 2019).
Examining the impact on pass-through is interesting, given evidence of declining productivity pass-through in Andrews et al (2019). As such, I also use a third rent-sharing specification:
- Rent sharing: The pass-through of productivity is a function of the labour market power and, therefore, concentration. This could be plant-level or market-level concentration:
Xi,t contains similar controls. In this case we can also include local market by time fixed effects, given the focus is not on the interaction between concentration and productivity.
5.2. Baseline results
Table 2 shows the results from the monopsony model. Running the model at the local labour market level (Local Labour Market model), we can see that increases in concentration are associated with lower wages, consistent with expectations. The coefficient is larger using the instrumental variable. This suggests that changes in the local HHI driven by national-level variation in concentration have a larger impact on wages and provide additional support to the baseline findings.
| Local Labour Market model | Plant-level model | ||||
|---|---|---|---|---|---|
| Monopsony | Monopsony – IV | Monopsony | Monopsony – IV | Oligopsony | |
| Productivity | 0.077*** (0.001) |
0.070*** (0.002) |
0.153*** (0.004) |
0.153*** (0.001) |
0.158*** (0.004) |
| Concentration – HHI | −0.122*** (0.008) |
−0.542** (0.253) |
−0.005 (0.011) |
−0.021** (0.009) |
|
| Concentration – plant market share | −0.103*** (0.027) |
||||
| R2 | 0.67 | 0.009 | 0.781 | 0.042 | 0.801 |
| N | 302,000 | 302,000 | 3,660,000 | 3,660,000 | 3,560,000 |
| Fixed effects | |||||
| Local market | Y | Y | Y | Y | N |
| Time*Industry | Y | N | Y | N | N |
| Time*Location | Y | Y | Y | Y | N |
| Time*Market | N | N | N | N | Y |
| Plant | N | N | Y | Y | Y |
| Note: All models contain controls for market size (number of workers in the market), and plant-level models account for number of plants in the parent firm. | |||||
The relationship is weaker if we regress plant-level wages on local labour market concentration (Plant-level monopsony models). This may reflect the fact that the model has difficulty accounting for plant-level variation in wages (and markdowns) using the market-level concentration metric. This suggests that the monopsony model might not be ideally suited to explaining firm-level wages.
The final column shows the results from the oligopsonistic model, where the concentration metric is the plant's share of employment in the local labour market. We see a significant negative relationship, consistent with firms setting a larger markdown and, therefore, lower wage, as they gain market share. This is the case even after accounting for market-level concentration, which will be captured in the fixed effect structure. So even within markets there is a great deal of variation in market power and markdowns.
Finally, Table 3 shows the results from the rent-sharing model. In all cases, pass-through from productivity to wages declines when concentration rises. Of particular interest, Column 3 shows the results when accounting both for market- and firm-level concentration. It shows that in more concentrated markets pass-through tends to be lower. But even within these markets there is variation, with larger firms having even lower pass-through.
| HHI | Firm Share | Both | |
|---|---|---|---|
| Productivity | 0.170*** (0.005) |
0.161*** (0.004) |
0.170*** (0.004) |
| Local Concentration (HHI)* Productivity | −0.194*** (0.016) |
−0.174*** (0.017) |
|
| Plant Concentration (plant share)* Productivity | −0.163*** (0.011) |
−0.074*** (0.01) |
|
| R2 | 0.797 | 0.796 | 0.797 |
| N | 3,560,000 | 3,560,000 | 3,560,000 |
| Fixed effects | |||
| Time*Market | Y | Y | Y |
| Plant | Y | Y | Y |
| Note: All regressions include a set of common controls covering firm characteristics (number of plants in the firm) and market characteristics (number of workers in the market). Errors clustered at the local market level. | |||
Figure 6 provides a sense of the magnitude of these results. Focusing first on the regressions using market concentration, wages are on average 4½ per cent lower in a highly concentrated industry (75th percentile HHI of 0.5), compared to a low concentration industry (25th percentile HHI 0.15). Equally, the degree of rent-sharing (the share of productivity changes passed on to wages) is around 1¾ percentage points lower in a high concentration industry. But gaps don't just exist across markets. Even within markets there is a great deal of difference between high and low market share firms. High market share firms pay wages that are 2 per cent lower (once accounting for differences in productivity and other factors), and the share of productivity passed on to wages for large firms is around 1½ percentage points lower.
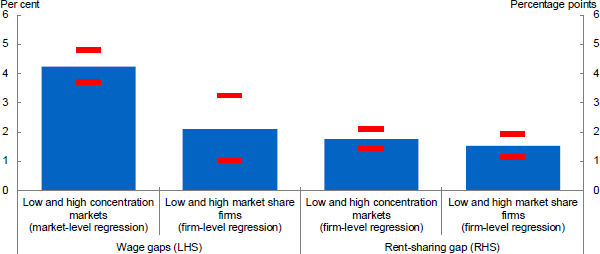
Note: Low and high concentration markets are the 25th and 75th percentile, respectively, and these differ across market versus firm specification due to differing firm counts per market. Low market share is zero, high market share is 20 per cent of market (95th percentile). Results from headcount models, either market-level or firm-level, as indicated. Red dashes show two standard deviation range of estimates.
Source: Author's calculations
This latter finding highlights the importance of firm heterogeneity when considering local labour market power. It also suggests that aggregate concentration measures may not be sufficient to consider changes in local labour market power. Instead, we may need to consider the full distribution of market shares, and how they have changed, to properly understand changes in market power and implications for wages.
5.3. Subsample results
As noted above, the degree of labour market concentration has been unchanged over the sample. At first blush, this would suggest that concentration cannot explain low wages growth pre-COVID. However, papers such as Benmelech et al (2022) have found evidence that the impact of given levels of concentration can change over time.
To examine this, I run the baseline market-level regression, but allowing all coefficients to vary across three financial year sub-samples: 2005–2007; 2008–2010 (GFC); 2011–2015 (post-GFC). This will allow me to consider whether the impacts of HHI on wages have increased, even if concentration has remained unchanged.[9]
Table 4 shows the results of the sub-sample regression. The impact of concentration more than doubled from the early period to the 2011–2015 period.[10]
| Baseline | Sub-sample | National Unemployment | State Unemployment | |
|---|---|---|---|---|
| Concentration | −0.122*** (0.008) |
−0.067*** (0.020) |
−0.123*** (0.015) |
−0.122*** (0.015) |
| Concentration * GFC | −0.076*** (0.021) |
|||
| Concentration * Post GFC | −0.079*** (0.022) |
|||
| Concentration * Unemployment | −0.359 (1.557) |
−0.035 (1.106) |
||
| R2 | 0.67 | 0.67 | 0.67 | 0.67 |
| N | 302,000 | 302,000 | 302,000 | 302,000 |
| Fixed effects | ||||
| Local market | Y | Y | Y | Y |
| Time*Industry | Y | Y | Y | Y |
| Time*Location | Y | Y | Y | Y |
| Note: All regressions include a set of common controls covering market characteristics (number of workers in the market). For GFC models, all controls other than firm FE are interacted with period dummies. Pre-GFC is 2005–2007. GFC is 2008–2010. Post GFC is 2011 to 2015. For unemployment models, interacting unemployment with productivity does not change the results. Errors clustered at the local market level. | ||||
One potential explanation could be softer labour markets. In many search-and-match models a tighter labour market leads to greater bargaining power for workers given the greater chance of finding another job, which could lower the impact of concentration. However, this does not appear to be the case, as there is no significant evidence that the impacts of concentration on wages are stronger when the labour market is weaker, as measured by the national or state-level unemployment rate (Columns 3 and 4).
To put the sub-sample result in perspective, Figure 7 shows the estimated wage gap between a high and low concentration markets for the early and recent periods. This gap is around to 2 per cent in the early period, but 5 per cent in the more recent period.
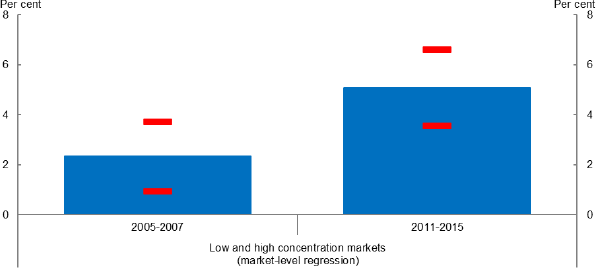
Note: Low and high concentration markets are the 25th and 75th percentile, respectively. Results from headcount models estimated at the market level shown over sub-samples in Table 5. Dashes show two standard deviation confidence interval. Interval for post period simply based on standard error of interaction term.
Source: Author's calculations
To get a sense of the macroeconomic impacts I use a simple back of the envelope calculation. The national employment-weighted average HHI is around 0.1. Multiplying this by the change in the HHI coefficient between periods (0.80) suggests that nationally wages were around 0.80 per cent lower than they would have been on average from 2011–2015, compared to the case whether the coefficient did not change. Given estimates put the ‘unexplained’ weakness in wages growth at around 0.25 per cent per year (Cassidy 2019), this suggests that the increasing impact of concentration can account for a large portion of the weakness in wages growth pre-COVID.
Obviously, the calculation is very simple and does not account for heterogeneity in outcomes or general equilibrium mechanisms. As such it should not be interpreted precisely. But it does suggest that the increasing impact of concentration has had a substantial effect on aggregate wages.
Footnotes
Search and match models such as Schubert et al (2021) also often reduce to such a characterisation. [7]
Results are also robust to using the lagged HHI to abstract from contemporaneous shocks. See Appendix B. Another approach would be to try to instrument using some ‘direct’ measure of changes in competition, such as mergers. However, such data are not available. [8]
These results are robust to changing the period definition. Note market fixed effects are not allowed to differ across samples, so variation in wages and HHI across sample periods is allowed to affect the results. So, we are in some senses identifying based both on whether changes in HHIs in the later samples had a larger impact on wages, as well as whether markdowns became relatively larger in more concentrated markets across the periods. Allowing the market fixed effects to vary and focusing on the former would be a stricter test but is not feasible due to the short sample period. Moreover, the latter aspect is also of relevance, particularly in thinking about the macro impact of the change. [9]
Excluding the mining sector does not impact the results. As such, it does not appear that the inclusion of the mining boom in the initial period is directly accounting for the results. [10]