Was the Additional Allowance Feature Effective? | RDP 2022-07: The Term Funding Facility: Has It Encouraged Business Lending?

RDP 2022-07: The Term Funding Facility: Has It Encouraged Business Lending? 6. Was the Additional Allowance Feature Effective?

Sharon Lai, Kevin Lane and Laura Nunn

December 2022

Download the Paper 2.1MB

6.1 Model specification

By exploiting the fact that banks received five times the additional allowance for lending to SMEs relative to large businesses, we examine whether the TFF was effective in stimulating growth in business credit. These regressions aim to identify only the effect of the additional allowance, without reflecting the effects of the TFF on lending via reducing funding costs and increasing funding certainty.

For our analysis examining the effect of the TFF on SME credit growth, we run our baseline specification for each month in the sample:

(1)

Δ L_{i j t} = \frac{C r e d i t ​ o u t s t a n d i n g_{i j t}}{A v e r a g e c r e d i t o u t s t a n d i n g_{i j J a n 2020}} \times 100 = α_{1} + α_{2} B o r r o w e r_{j} + ε_{i j t}

The dependent variable $Δ L_{i j t}$ is the cumulative growth in business credit by bank i to borrower type j in month t relative to a pre-TFF period (average of the three months to January 2020). Borrower_j is a dummy variable equal to 1 for SMEs and 0 for large businesses. The coefficient $α_{2}$ represents our treatment effect. This approach is approximately equivalent to a panel regression with time-specific coefficients on the borrower type, and fixed effects for the pre- and post-TFF periods.^[13]

We run a version of our baseline regression using fixed-term lending as the dependent variable, although this uses a smaller sample of banks. As a ‘placebo test’, we also run a version of the baseline model for small business lending relative to medium business lending.^[14]

In order to control for the uneven effects of COVID-19 across industries, we run versions of these models at the bank-industry level. The bank-industry level model specification is similar to the baseline model, with data organised at the bank i and industry k level and the inclusion of a bank × industry fixed effect $θ_{i k}$ :

(2)

Δ L_{i j k t} = \frac{C r e d i t ​ o u t s t a n d i n g_{i j k t}}{A v e r a g e c r e d i t o u t s t a n d i n g_{i j k J a n 2020}} \times 100 = α_{1} + α_{2} B o r r o w e r_{j} + θ_{i k} + ε_{i j k t}

This specification absorbs the effects of any shocks that affect an entire industry (e.g. retail), or a particular institution, or even shocks that affect the lending of a particular institution to a particular industry. As such, this specification is more robust to the potential violations of the parallel trends assumption discussed above.

There are several small institutions in our sample that may be driving our results, particularly those that experienced growth in business credit off a very low base. We address this by removing two outliers (these banks did not access the TFF). As a further check, we weight the regressions for the baseline model and the industry-level model by each institution's level of business credit in the base period. We also run weighted regressions that have been limited to just fixed-term lending.

We explore if the effects of the TFF differed depending on bank characteristics. We add the bank characteristic, Characteristic_n , and the characteristic interacted with the SME borrower dummy, one at a time into our baseline specification:

(3)

\begin{array}{l} Δ L_{i j t} = \frac{C r e d i t ​ o u t s t a n d i n g_{i j t}}{A v e r a g e c r e d i t o u t s t a n d i n g_{i j J a n 2020}} \times 100 = β_{1} + β_{2} B o r r o w e r_{j} + β_{3} C h a r a c t e r i s t i c_{n} \\ + β_{4} (B o r r o w e r_{j} \times C h a r a c t e r i s t i c_{n}) + ε_{i j t} \end{array}

This specification uses a smaller sample size of banks than our baseline regression, given the available data on bank characteristics.

We also take a standard difference-in-difference model and add bank and period fixed effects, $θ_{i}$ and $θ_{t}$ , respectively:

(4)

\ln (l_{i j t}) = α_{1} + α_{2} (T F F_{t} \times B o r r o w e r_{j}) + θ_{i} + θ_{t} + ε_{i j t}

Given the potential issues around the validity of using large business lending as a control group for SME business lending, we run a model in the spirit of a triple-difference regression examining lending to SMEs relative to large businesses and examining lending by banks relative to non-banks. The specification is:

(5)

\begin{array}{l} Δ L_{i h j t} = \frac{C r e d i t ​ o u t s t a n d i n g_{i h j t}}{A v e r a g e c r e d i t o u t s t a n d i n g_{i h j J a n 2020}} \times 100 = y_{1} + y_{2} B o r r o w e r_{j} + y_{3} i n s t i t u t i o n_t y p e_{h} \\ + y_{4} (B o r r o w e r_{j} \times i n s t i t u t i o n_t y p e_{h}) + ε_{i h j t} \end{array}

Here, the coefficient of interest is y₄. This coefficient reflects the effect of the TFF on the difference between SME and large business lending for banks relative to non-banks. The dependent variable $Δ L_{i h j t}$ is the cumulative growth in business credit by bank i of institution type h to borrower type j in month t relative to a pre-TFF period (average of the three months to January 2020), where institution_type_h is a dummy variable equal to 1 for banks and 0 for non-banks. This specification uses a larger sample than the specifications above, with non-banks included.

6.2 Results

For most of our models, estimation is between October 2019 and October 2021, with the sample varying depending on the model specification and data used. By running a separate regression for each month in our sample, we are able to estimate a TFF effect for each period rather than constraining the effects to be constant over time. Standard errors are clustered at the institution level. All results tables can be found in Appendix C.

In our baseline model (Equation (1)), we find no statistically significant effects of the TFF on credit growth to SMEs relative to large businesses for all time periods following the introduction of the TFF up until additional allowances were calculated in April 2021 (Table C1).^[15] The coefficients for our baseline model represent the difference in cumulative growth, relative to the pre-TFF period, between credit outstanding to SMEs and large businesses. For example, taken at face value, the coefficient for April 2021 suggests that the TFF caused cumulative growth in SME credit to be 3.7 percentage points higher than for large businesses (Figure 10). However, the confidence intervals are wide.

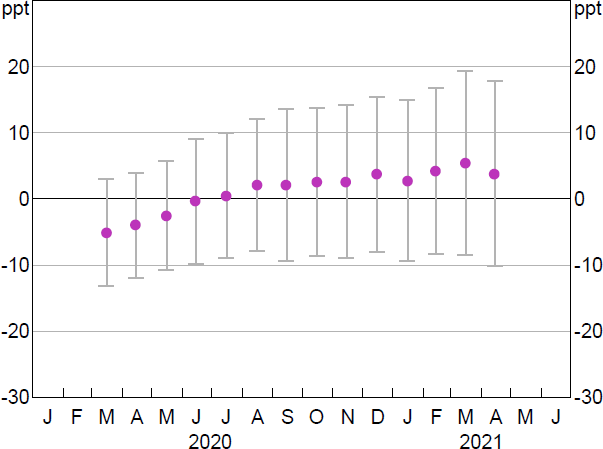
Figure 10: Bank Credit Growth to SMEs Relative to Large Businesses

Regression coefficient

The coefficients are negative in early 2020, indicating that credit increased for large businesses relative to SMEs. This reflects that large businesses drew down on lines of credit as the pandemic intensified. Limiting the baseline model to fixed-term lending causes the coefficients to be higher in early 2020. However, there are no statistically significant effects of the TFF on fixed-term credit growth to SMEs relative to large businesses for all time periods following the introduction of the TFF (Figure B1; Table C2).

In contrast to what we would expect, our ‘placebo test’ – which is a version of our baseline model for lending to small businesses relative to medium businesses – generates significant and negative coefficients on the small business borrower dummy for the most recent few months in our sample (Figure B2; Table C3). This negative correlation between business size and lending is consistent with the perverse negative coefficient estimates we find in our baseline models; it suggests that lending to large firms is not a good counterfactual for lending to smaller firms during the period being studied.

The industry-level model (which, as discussed above, is intended to control for the uneven effects of COVID-19 by industry; Equation (2)) finds no statistically significant effects for most time periods, although there are some statistically significant, negative coefficients in the earlier months following the TFF introduction (Figure B3; Table C4). This is the opposite sign to what we would expect a priori. Our preferred specification has an interaction between bank and industry dummies, which allows us to examine the difference in SME and large business credit growth for a particular bank within a particular industry. As a crosscheck, we also run variations of the model with only bank-level fixed effects and only industry-level fixed effects (Figures B4 and B5; Tables C5 and C6). The results of these model variations are consistent with our preferred specification, with statistically non-significant effects for most time periods, except the earlier months of the pandemic where large negative significant coefficients are recorded on the SME borrower treatment variable. These were the months in which large businesses drew down on lines of credit for precautionary reasons.

In the regressions that are weighted by each institution's level of business credit in the base period, the coefficients on the SME borrower term are negative and statistically significant in multiple time periods for both the baseline model specification and the industry-level model (Figures B6 and B7; Tables C7 and C8). This is unsurprising given that, in aggregate, SME business credit growth has generally been weaker than large business credit growth, particularly in the early months of the COVID-19 pandemic as large businesses drew down on lines of credit to shore up liquidity positions. For our weighted regressions that have been limited to just fixed-term lending, the coefficients on the SME borrower term are negative and statistically significant in multiple time periods (Figure B8; Table C9).

We also explore whether the effects of the TFF differed depending on bank characteristics (as at December 2019, prior to the TFF; Equation (3)). Some of these regressions have the full sample of up to 50 banks, but three regressions – those using the common equity tier 1 capital ratio, total tier 1 capital ratio and tier 1 leverage ratio – include only 14 banks. For simplicity, we run the analysis for just one time period (April 2021) and add the bank characteristics (the characteristic itself and the characteristic interacted with the SME borrower dummy) one at a time into our baseline specification. These models present statistically insignificant results for almost all model variations (Table C10). However, we find a statistically significant and positive coefficient for the interaction between capital ratios and SME lending. At face value, this suggests that banks with higher capital ratios prior to the TFF experienced stronger cumulative growth in lending to SMEs relative to large businesses in April 2021, though the results should be interpreted with caution given the small sample size of this specification.

Our standard difference-in-difference model with bank and period fixed effects (Equation (4)) generates a negative and not statistically significant coefficient on the interaction term (Table C11). This aligns with our baseline model, which also indicates that there was no statistically significant effect of the TFF credit growth to SMEs relative to large businesses.

In the triple-difference model (Equation (5)), the coefficient on the interaction term reflects the effect of the TFF on banks' lending to SMEs less large businesses, relative to non-banks. We would expect the gap between growth in SME and large business lending to be larger for banks, relative to non-banks. The coefficient on the interaction term is negative and weakly statistically significant, suggesting the opposite result: the difference between SME and large business lending decreased for banks, relative to non-banks (Figure 11; Table C12). However, large and increasing confidence intervals suggest that our estimates are too imprecise to determine whether this trend holds over the whole sample.

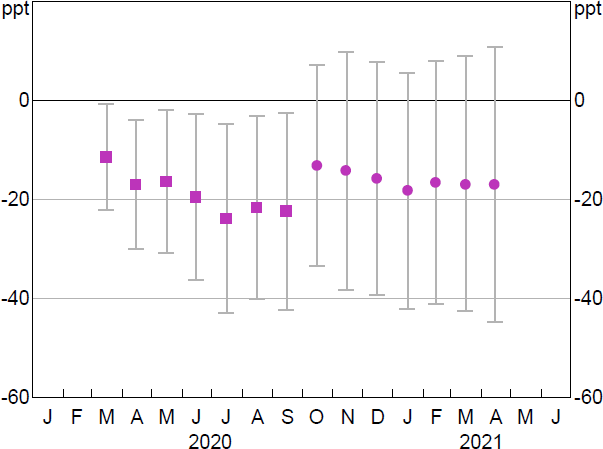
Figure 11: Bank Credit Growth to SMEs Relative to Large Businesses and for Banks Relative to Non-banks

Regression coefficient

Footnotes

This approach follows Berger, Turner and Zwick's (2020) evaluation of the First-Time Homebuyer Credit policy and Mian and Sufi's (2012) assessment of the Cash for Clunkers program. [13]

The TFF additional allowance encouraged lending to small businesses and medium businesses equally, so we should not expect to find a differential effect on credit to these business size types. [14]

As mentioned earlier, this model uses data on SME and large business credit outstanding reported by 15 banks directly to the RBA from November 2019 until April 2021. As such, results for our full sample of banks is only available to April 2021, rather than October 2021 as presented in most of our regressions. As additional allowances were finalised in April 2021, it is unlikely that they would continue to directly stimulate growth in business credit beyond this date. [15]