RDP 2022-07: The Term Funding Facility: Has It Encouraged Business Lending? 8. Did a Lender's Take-up of the TFF Affect Their Business Lending?
December 2022
- Download the Paper 2.1MB
8.1 Model specification
Our final set of models investigates whether a lender's growth in business lending was affected by whether or not they accessed funding through the TFF; this is in contrast to the results above, which reflect the availability of the TFF.[16] Similar to the regressions in Section 7, these results capture the full range of channels through which the TFF can affect business lending.
In our first specification, we examine aggregate business credit growth for eligible banks that accessed the TFF compared to banks that did not. These units of analysis are more consistent with international studies, which commonly evaluate outcomes in participating versus non-participating institutions. We begin with a simple OLS specification that is similar to the previous two models:
where accessedTFFi is a binary variable for whether or not a bank accessed the TFF.[17]
However, this gives rise to an endogeneity issue because participation in the TFF was voluntary. As discussed above, we address this through instrumental variables. Firstly, we instrument participation in the TFF with the availability (or adequacy) of self-securitised assets at the beginning of the TFF, using a sample of just banks.[18] The first-stage and instrumental variable specifications are as follows:
where self_secs is either: a binary variable equal to 1 for when a bank has self-securitised assets; or a measure of the adequacy of a bank's self-securitisations (the value of self-securitised assets as a share of the bank's total cash limit).
We also address the endogeneity issue by instrumenting participation in the TFF with a lender's eligibility to access the TFF, using our full sample of bank and non-bank lenders. The first-stage and second-stage specifications are as follows:
where institution_typeh is a binary variable equal to 1 if the institution is a bank and 0 if the institution is a non-bank. This is similar to the instrumental variable regression above using self-securitisations, albeit with a different sample and different set of institutions captured by the estimated treatment effect.
8.2 Results
We start our third analysis by running the basic OLS regression, which compares business credit growth between banks that accessed the TFF and those that did not (Equation (7)). We find no statistically significant effects of accessing the TFF on credit growth (Table C19). The coefficients in this model are volatile around zero, with wide confidence intervals (Figure B14).
However, as discussed above, voluntary participation in the TFF could give rise to an endogeneity issue in this analysis, as it is possible that banks who accessed TFF funding may have increased lending anyway. As such, we address this through instrumental variables. Firstly, we extend the basic OLS regression above by instrumenting participation in the TFF with the availability (or adequacy) of self-securitised assets at the beginning of the TFF. In this model, the first-stage regressions suggest that the availability and/or adequacy of self-securitised assets had a positive and statistically significant effect on whether a bank accessed the TFF, consistent with our expectations (Equation (8)). The t-statistics on the instrument are 5.9 in the model with the binary instrument and 4.3 in the model using self-securitisation adequacy, suggesting the weak instrument test is passed based on the rough rule of thumb of t > 3.16 (Tables C20 and C22).[19] Our second-stage estimates of the effect of the bank accessing the TFF on business lending are generally negative but not statistically significant (Equation (9); Figures 13 and B15; Tables C21 and C23). Our second-stage coefficients also have wide Anderson–Rubin confidence intervals.[20]
As expected, the coefficients in our second-stage regression are generally lower when compared with the coefficients found in our basic OLS version. This is consistent with banks accessing the TFF because they expected to increase lending.
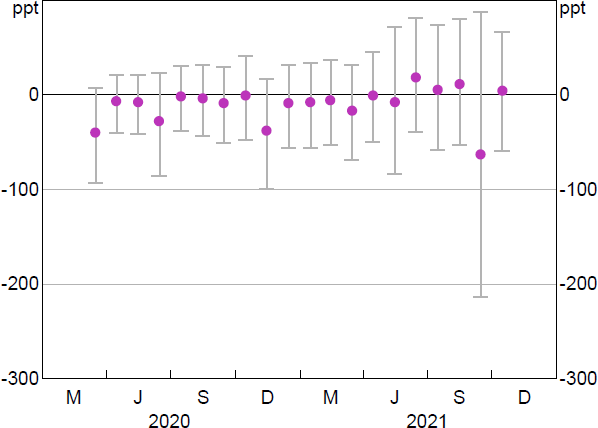
Note: Whiskers show Anderson–Rubin 95 per cent confidence intervals.
Sources: APRA; Authors' calculations; RBA
We repeat the above regressions comparing lending between banks that accessed the TFF and those that did not, but this time using only fixed-term lending (i.e. excluding revolving credit lines). This uses data from the ARF 742_0 A/B form, which has the breakdown of business credit by finance type but a smaller sample of institutions. The first-stage regressions suggest that the availability and/or adequacy of self-securitised assets had a positive and statistically significant effect on whether or not a bank accessed the TFF, consistent with our expectations. The t-statistics on the instrument are 3.1 in the model with the binary instrument and 2.9 in the model using the self-securitisation adequacy, suggesting the instruments may be weak (Tables C24 and C26). Again, we find no statistically significant effect of accessing the TFF on lending for all time periods following the introduction of the TFF (Figures B16 and B17; Tables C25 and C27).
We also instrument participation in the TFF with a lender's eligibility to access the TFF, using our full sample of bank and non-bank lenders. In this model, the first-stage regression (Equation (10)) suggests that, unsurprisingly, eligibility to access the TFF had a positive and statistically significant effect on whether a bank accessed the TFF (Table C28). The t-statistic on the instrument is 17.36, suggesting the weak instrument test is comfortably passed. As expected, our second-stage regression (Equation (11)) finds results similar to the effects of the availability of the scheme but scaled upwards (Figure 14; Table C29). These coefficients are generally positive but are, in most cases, statistically insignificant.
In principle, any difference between these results and those using self-securitisations could reflect differences in samples and differences in the institutions captured by the estimated treatment effect.[21] In any case, the coefficients are statistically insignificant across both results.
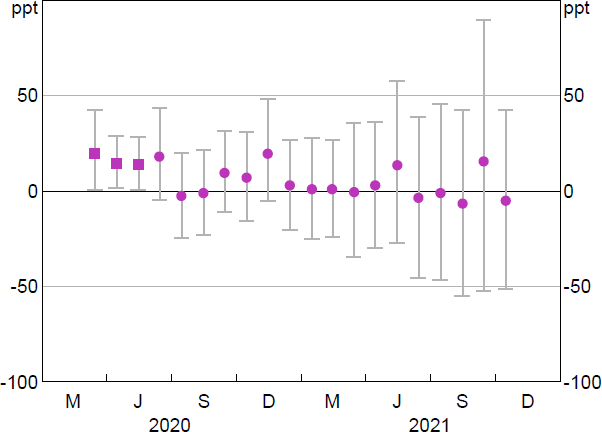
Notes: Whiskers show Anderson–Rubin 95 per cent confidence intervals. The filled square marker indicates a significant result.
Sources: APRA; Authors' calculations; RBA
Footnotes
The model in Section 7 estimates an intention-to-treat effect, while this model is the average treatment effect on the treated (ATT). [16]
For simplicity we assign this a value of 1 for institutions that accessed the TFF by the end of the drawdown period (i.e. we do not identify whether an institution had accessed it by a particular time period). [17]
We considered a version of Equation (8) where the dependent variable was bank-level drawdowns of the TFF in value terms; this would have allowed us to evaluate the effect of actual drawdowns of the TFF (in contrast with simply accessing some level of funding through the TFF). However, the strength of self-securitised assets as an instrument was considerably weaker in this regression. [18]
However, more recent studies suggest that the threshold for instrument validity needs to be much higher, so it is possible that we still have a weak instrument problem. [19]
Anderson–Rubin confidence intervals, or weak instrument-robust confidence intervals, provide a valid measure of uncertainty even if our instruments are weak (Anderson and Rubin 1949). We use these confidence intervals for our instrumental variable analysis. [20]
The first instrumental variable regression, using self-securitisations, is intended to estimate the treatment effect among those banks that accessed the TFF only because they had self-securitisations on their balance sheet. The second instrumental variable regression captures the treatment effect for banks that accessed the TFF, regardless of whether or not they had self-securitisations. In other words, the set of ‘compliers’ is different between the two models. [21]