RDP 2022-01: MARTIN Gets a Bank Account: Adding a Banking Sector to the RBA's Macroeconometric Model 2. BA-MARTIN in a Nutshell
January 2022
- Download the Paper 1,775KB
The mechanics of the new banking sector in MARTIN can be summarised as follows (see Figure 1 for a graphical representation):
- Higher unemployment, lower housing prices and higher interest rates all increase loan losses.[1]
- These loan losses directly reduce banks' profits; with sufficiently large losses causing banks' capital to fall. Losses also increase the perceived riskiness of banks' loan portfolios, so the risk weights attached to assets when determining banks' capital adequacy ratios (capital divided by risk-weighted assets) increase.
-
Australian banks hedge the majority of their interest rate risk (Brassil et al 2018). Therefore, the direct effects of interest rate changes on banks' profits can be decomposed into three components: changes in the cash rate, changes in banks' debt/deposit funding spreads and changes in the spreads between their lending rates and funding rates.
- Funding spreads are determined by offshore funding markets (as in Brassil et al (2018)), changes in credit risk (determined by changes in capital adequacy) and a zero lower bound (ZLB) for retail deposits. For a given level of lending spreads, a reduction in funding spreads or the cash rate directly reduces banks' net interest margins (NIM = net interest income divided by interest-earning assets), because banks have more interest-earning assets than interest-bearing liabilities.
- Lending spreads consist of an exogenous component (the determinants of which include competitive pressures and regulations, for example) – denoted as the ‘unconstrained lending spread’ in Figure 1 – and an endogenous response to a deterioration in capital adequacy (discussed below). A reduction in lending spreads also reduces banks' NIMs, but the effect is much larger than the effect of a funding cost change because banks have more debt than equity.
- Banks can respond to a capital deterioration in several ways; these include: raising new capital (e.g. equity issuance), reducing dividends, increasing lending spreads and reducing their willingness to lend. We assume that banks do not immediately raise new capital in response to a widespread capital deterioration.[2] Therefore, once dividend payments are minimised, banks' only remaining options for returning their capital adequacy ratios to target are to increase lending spreads and/or reduce credit growth.
-
In the baseline version of BA-MARTIN, we assume banks choose to increase lending spreads on new and outstanding loans in response to a capital deterioration.[3] We make this assumption because increasing lending spreads increases banks' NIMs, which profit-maximising banks desire.
- Prior to the capital deterioration, competition prevents banks from increasing lending spreads. The capital deterioration allows banks to increase these spreads without fear of losing market share (because there are barriers to entry and we model a deterioration that affects all banks). In other words, banks are constrained profit-maximisers whose capital constraints tighten as a result of the losses, thereby increasing their constrained profit-maximising lending spreads.
- MARTIN already has an equation that determines the relationship between lending rates and household credit growth; this equation is estimated from the historical relationship between these variables. To minimise the changes we make to MARTIN, we do not change this equation.[4] Therefore, by increasing their lending spreads (i.e. by reducing credit supply), banks increase NIMs and reduce credit growth, both of which increase their capital adequacy ratios.
- This reduction in credit supply feeds back into the real economy and amplifies losses – directly by increasing debt servicing costs and indirectly via lower housing prices and higher unemployment (i.e. the banking sector amplifies the original economic deterioration).
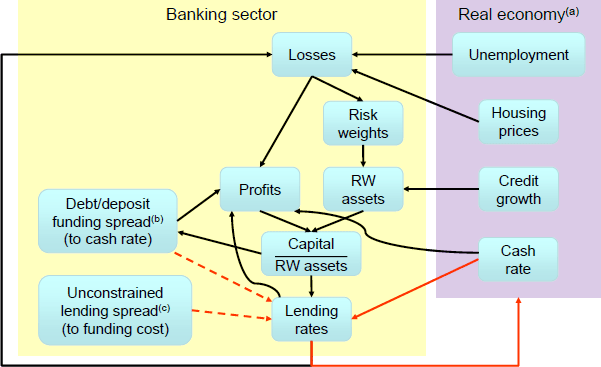
Notes:
Solid red arrows denote unchanged MARTIN relationships, dashed red arrows denote existing MARTIN relationships that we endogenise, and black arrows denote the new relationships. RW = Risk-weighted.
(a) Links within the real economy are excluded for simplicity.
(b) Including a zero lower bound for retail deposits.
(c) The spread banks would set if capital levels were at their desired level.
In short, we model the financial accelerator mechanism in a piecewise fashion. If losses are small and banks' capital is sufficiently high, credit growth is demand determined – that is, lending rates equal an exogenous spread over the cash rate – and the effect these losses have on the broader economy is limited to that caused by the lower shareholder returns (as is currently the case in MARTIN). Conversely, if loan losses are sufficiently large to cause banks' capital to fall below their desired level, an endogenous and nonlinear wedge forms between the actual lending spread and the exogenous spread – that is, credit supply is endogenously reduced.
Importantly, this feedback into the real economy can be offset by more expansionary monetary policy (if monetary policy is unconstrained). With this expansionary policy also leading to reduced loan losses, thereby improving capital adequacy. However, the more expansionary policy also leads to higher credit growth and a reduction in NIMs, both of which amplify the deterioration in capital adequacy. Which channels dominate will depend on the state of the economy (and is the subject of Section 5 of this paper).
How much banks reduce credit supply in response to a capital deterioration is based on the RBA's stress testing framework (RBA 2017). This framework is more complex than what could reasonably be incorporated within a macroeconometric framework. So instead of matching the stress testing framework exactly, we assume banks reduce credit supply in order to return their capital ratios to target with a speed of adjustment that broadly matches the speed of adjustment implied by the stress testing framework. This speed of adjustment is detailed in Section 3.8.
2.1 Alternative assumption: credit supply reduction affects new loans only
Instead of our baseline assumption that banks reduce credit supply by increasing lending spreads on new and outstanding loans, BA-MARTIN is sufficiently flexible to allow exploration of a scenario in which banks impose the cost of restoring capital adequacy on new loans only (e.g. by tightening lending standards). While we think this is less likely to be the response of Australian banks (due to the features of Australia's banking system, see Section 1), such a response is more consistent with the experience of major banking systems during the global financial crisis (Maddalonia and Peydró 2013; Bassett et al 2014), and is therefore an important scenario to be able to model.
With this alternative assumption, banks' credit supply reductions have only marginal direct effects on their NIMs (as NIMs are determined by outstanding loans). Therefore, banks are only able to directly increase their capital ratio by reducing credit growth (i.e. through the denominator of the capital ratio). With the credit supply reduction working through the denominator only, achieving the same increase in the capital ratio requires a much larger reduction in credit supply, resulting in a much larger financial accelerator mechanism than with our baseline assumption.
Only minor changes to BA-MARTIN are required to implement this alternative assumption. Instead of reductions in the capital ratio directly leading to increases in all lending spreads (Figure 1), banks' reduce credit growth by increasing the cost of some new borrowing, thereby reducing the amount people are willing to borrow. These reductions in credit growth reduce investment and housing prices, ultimately leading to higher unemployment and feeding back into higher losses.
In reality, housing prices, investment and credit growth are determined by the lending rates available for new loans. Therefore, the original MARTIN relationship between household credit growth and lending rates remains unchanged with this alternative assumption. However, any changes in lending standards will have a material effect on this relationship.
For example, if banks reduce credit supply across the risk spectrum, then the MARTIN relationship between credit growth and new lending rates remains unchanged. However, if riskier loans become relatively more costly (i.e. lending standards are tightened), then the credit quality of the average new loan would increase, such that average lending rates would increase by less than the MARTIN relationship would suggest. A neat feature of our framework is that we are able to incorporate this increased flexibility into the credit growth-lending rates relationship without changing any of the original MARTIN equations (our approach is detailed in Section 3.8.3).
Footnotes
We define ‘losses’ as the flow of provisions and unexpected loan write-offs (see Section 3.1 for further explanation). [1]
More accurately, we assume that when the whole banking system suffers a capital deterioration, the cost of raising new capital would be sufficiently prohibitive that banks would not choose this option. [2]
For simplicity, we assume there are barriers to entry, and that banks are homogeneous and suffer proportional capital deteriorations. With the majority of loans in Australia being variable-rate loans, we further simplify the model by assuming all loans have variable rates and that switching lenders is costless. Combined, these assumptions mean profit-maximising banks will maintain equivalent interest rates on new and outstanding loans in equilibrium (in reality, market power and switching costs permit a small differential between new and outstanding lending rates). [3]
We are implicitly assuming that over MARTIN's estimation period the credit supply curve was flat (i.e. the curve shifted with funding costs, but the interest rates set by banks were unrelated to quantities). This is a reasonable assumption for most of the estimation period, given Australian banks' persistently high credit quality. However, this assumption was likely violated during 2015–18, when quantity-based regulatory restrictions were placed on investor and interest-only loans (APRA 2019). [4]