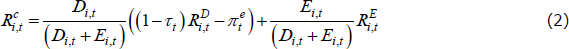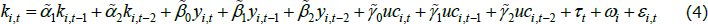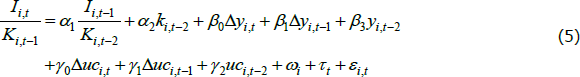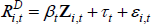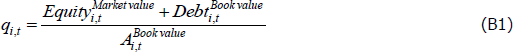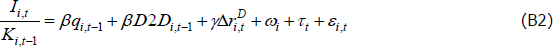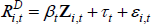Research Discussion Paper – RDP 2018-05 Do Interest Rates Affect Business Investment? Evidence from Australian Company-level Data
1. Introduction
‘… it is well known that to get the user cost to appear at all in the investment equation, one has to display more than the usual amount of econometric ingenuity, resorting most of the time to choosing a specification that simply forces the effect to be there.’ (Blanchard 1986, p 153)
Modern macroeconomic textbooks typically suggest that there is an inverse relationship between interest rates and business investment (e.g. Mankiw 2007; Blanchard 2017). In the textbook description, this inverse relationship is essential to understanding how changes in monetary policy affect the economy.
Despite its theoretical importance, as the quote above suggests, empirical evidence for this inverse relationship is difficult to establish. In surveys, businesses themselves argue that their investment decisions are not affected by changes in the cost of borrowing. This is because these businesses have very high and sticky hurdle rates of return (Sharpe and Suarez 2014; Lane and Rosewall 2015). More generally, modelling business investment is inherently difficult, particularly with aggregate time-series data (e.g. Chirinko 1993; Caballero 1999; Hassett and Hubbard 2002; Cockerell and Pennings 2007).
Investment is a heterogeneous activity. At any point in time, some businesses are investing a lot while others are not investing at all. As such, empirical studies that exploit this heterogeneity at a company level typically have more success in modelling business investment (e.g. La Cava 2005; Gilchrist and Zakrajšek 2007). Company-level data can also help to ameliorate some of the endogeneity that arises in time-series analysis. For instance, central banks tend to raise interest rates in periods of strong economic activity when investment is high (and vice versa). This reverse causality makes it harder to identify a negative correlation between interest rates and investment using aggregate data.
But even in micro data studies it can be hard to pin down the causal effect of interest rates on investment. There are several sources of potential endogeneity. First, omitted variables may drive the correlation between the cost of debt and investment. For example, risky companies are likely to pay relatively high interest rates. But risky companies may be more likely to invest than other companies if they have better growth prospects. This would lead to a positive correlation between company-level interest rates and investment. Second, there may be sample selection bias. The cost of debt is only observed for companies that have taken on debt. Hence the sample is limited to indebted companies. The decision to apply for (and be granted) debt may be correlated with the decision to invest; as such, companies with debt may invest more (or less) than other companies. The sensitivity of investment to interest rates may also differ for companies with and without debt.
An additional challenge in identifying the effect of interest rates on investment is that company-specific information on interest rates is not readily available in standardised company reports. Instead, research typically relies on proxies for the implied interest rate facing a company. These proxies include the ratio of interest expenses to the stock of debt (La Cava 2005), corporate bond rates (Gilchrist and Zakrajšek 2007) or business borrowing indicator rates more generally.
A key contribution of this paper is to provide direct company-specific estimates of the cost of debt. These data are hand collected from the notes to company annual reports. Australian companies are required to report how they manage risks, including liquidity and interest rate risks. As part of this reporting, most Australian companies provide information on the interest rate payable on each debt instrument that they hold.
Our interest rate estimates are an improvement on the existing literature in at least three respects. First, unlike aggregate time-series indicators such as business indicator rates, our estimates capture the cross-sectional heterogeneity in rates faced by companies (and how this heterogeneity changes over time). Second, our estimates are closer to the theoretical concept of the marginal cost of debt than are more conventional measures such as the ratio of interest paid to the stock of debt. This ratio can be heavily influenced by companies choosing to pay down debt during the year. For example, a company that chooses to make excess repayments in a year may be wrongly classified as facing a high interest rate. Our measure reflects rates at the end of the financial year and so should be less affected by such distortions. Third, our company-specific estimates are broader than those used in previous research as they cover not only corporate bond issuance but intermediated bank debt too.
An additional contribution of this paper is to demonstrate the importance of controlling for sample selection when studying investment using company-level data. The existing company-level research typically relies on estimates of interest rates that are calculated on existing holdings of debt, thereby restricting the sample to indebted companies. We explicitly address this sample selection issue through multiple imputation techniques. To the best of our knowledge, this has not been done before in the business investment literature.
Exploiting our novel dataset, three main observations emerge:
- There is a large degree of heterogeneity in the interest rates paid by Australian companies. Since 2004, the gap between the top and bottom deciles has been around 5 percentage points, on average. Moreover, since the global financial crisis, the spread between the rates paid by companies at the top and bottom of the distribution has widened, with rates for the top decile of companies (the ‘riskier’ companies) having remained high in recent years despite falls in the cash rate and in aggregate indicators of business lending rates.
- There is a strong and robust inverse relationship between the marginal cost of finance and investment for companies with debt. A 1 per cent decrease in the interest rate paid on debt is associated with the investment rate (investment divided by the previous period's capital stock) rising by ¼–½ percentage points, on average.
- By controlling for sample selection through multiple imputation techniques, we find some evidence that companies with debt are significantly more sensitive to interest rates than those without debt. This puts into question the external validity of papers that focus solely on companies with debt, and suggests that the elasticities of investment with respect to interest rates estimated in these papers should not be generalised to the full universe of firms.
Taken together, our results suggest that, in contrast to the Blanchard (1986) quote, you do not need econometric ingenuity but, rather, good data to identify the link between interest rates and business investment. The results also provide a partial explanation for why, up until recently, non-mining investment has been relatively weak: despite the fact that policy rates and indicators of aggregate lending rates are low, interest rates for up to a fifth of companies remain reasonably high.
Our results do not establish why there is a link between interest rates and investment because it is difficult to identify a plausibly exogenous source of interest rate variation. The negative relationship between interest rates and investment does not appear to reflect changes in monetary policy, at least not directly, as we control for this in the analysis. The relationship is also not due to variation in company risk, as we control for this too. Instead, we believe it is due to credit supply effects; a relaxation of lending standards leads to lower interest rates (for a given company profile) and boosts investment.
2. Data and Stylised Facts
2.1 Sample Construction
Our analysis focuses on a random sample of 100 non-financial non-resource companies that are publically listed on the Australian stock exchange. Balance sheet, profit and loss statement, and cash flow statement data are obtained from Morningstar. Equity market data, which are used in constructing the cost of equity and finance, are obtained from Bloomberg and the Center for Research in Security Prices. We hand collect information on company-specific interest rates based on the notes to listed companies' annual reports.
Australian listed companies are required to report how they manage their liquidity and interest rates risks in the notes to their annual reports. But, unlike balance sheet information, the notes on liquidity and interest rate risks are not reported in a standardised way across companies. The lack of consistency in how companies report the data may introduce measurement error. For instance, some companies report very detailed information on the interest rates that they pay on each of their debt instruments, other companies report only a weighted average interest rate, while some companies do not report interest rates at all. Also, companies differ in how they report their interest rate hedging activities. Some report the ultimate rate they face, while others report rates on the borrowing, as well as on the fixed- and floating-rate legs of their swaps.
To check for potential measurement error, we compare our hand-collected estimates to more conventional implied measures such as the ratio of interest payments to debt. Our estimates are broadly similar, which gives us confidence that we are capturing genuine variation in the cost of debt across companies. Moreover, the estimates were cross-checked by researchers that were not involved in the original data collection process.
The sample period covers the years 2004 to 2015. We do not restrict the sample to companies that survive for the entire period. Instead, we allow companies to both enter and exit the sample.[1] This minimises ‘survivorship’ bias, which occurs when delisted companies are excluded from the sample, leading to an unrepresentative sample of companies. This is potentially important as the characteristics of a company that determine its survival may also be associated with its investment and financing decisions (e.g. degree of risk aversion or governance structure).
As not all companies have debt (or report interest rates) in each year, we have interest rate data for 40–50 companies for each year of the sample period.
Overall, the sample appears representative of the universe of listed Australian non-financial non-resource companies. This is true across a wide range of metrics, from age to size to gearing (see Appendix A). Admittedly, the focus on listed companies means that the sample is skewed towards larger companies. But this is true of much of the existing research that explores the relationship between the cost of finance and investment. Moreover, the investment of listed companies could plausibly be less sensitive to the cost of finance than that of other businesses if they are less financially constrained, on average. This would imply that our results underestimate the effect of the cost of finance on aggregate investment.[2] Also, our estimates indicate that aggregate investment by non-financial non-resource listed companies is equivalent to around half of total capital expenditure by non-resource companies in Australia.[3] This suggests that our results are likely to be important for understanding developments in aggregate business investment.
2.2 The Cost of Debt
We measure the cost of debt as the weighted average borrowing rate paid by a company on their outstanding debt instruments at the end of their financial year.[4]
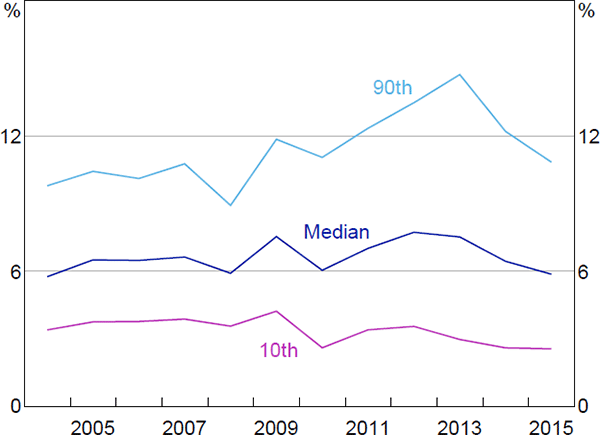
There is significant heterogeneity in the borrowing rates paid by companies. For instance, in 2015, a borrowing company could be paying an interest rate as high as 10 per cent (at the 90th percentile) or as low as 4 per cent (at the 10th percentile).
This distribution of company borrowing rates has also changed a lot over time. The median borrowing rate paid by companies in our sample has declined to its lowest level since 2004, alongside the cash rate and aggregate indicators of business lending rates (Figure 1). The 10th percentile rate has followed a similar pattern, while the 90th percentile rate remains around its sample average, though it has declined from its peak. This has resulted in the spread between the 90th percentile rate and the median rate, and between the 90th percentile rate and the 10th percentile rate, increasing by around 3 percentage points between 2004 and 2015. The increase in spreads occurred during the financial crisis and the European debt crisis, and has not been unwound. Similar patterns are evident for other deciles towards the top of the distribution.
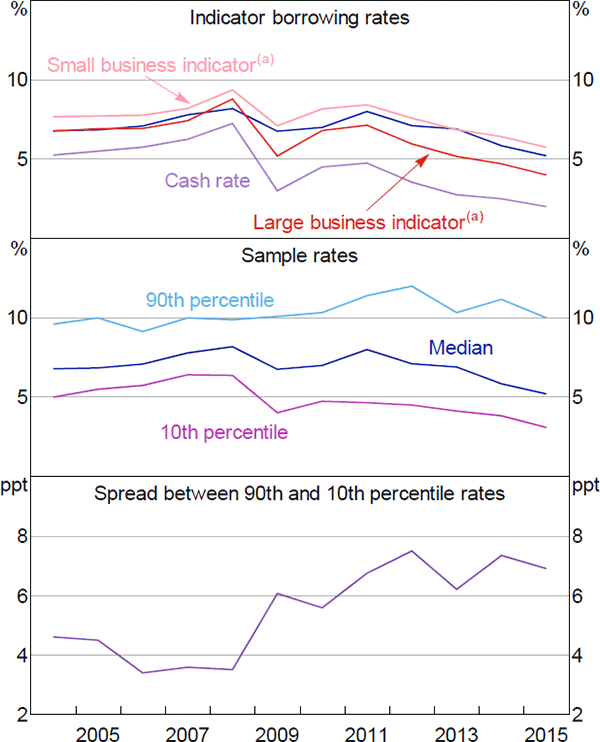
Note: (a) Average bank borrowing rates; small business indicator is average rate on loans below $2 million; large business indicator is average rate on loans above $2 million
Sources: APRA; Authors' calculations; Company reports; RBA
The variation in borrowing rates across companies is likely to be related to variation in the perceived credit risk of each company.[5] Here, we examine how the borrowing rates vary with two key risk characteristics: company size and distance to default.
We find that large companies tend to pay lower interest rates on their debt relative to small companies (Figure 2). This is consistent with large companies being less likely to fail and hence being perceived to be less risky by creditors (e.g. Dunne, Roberts and Samuelson 1988; Kenney, La Cava and Rodgers 2016).
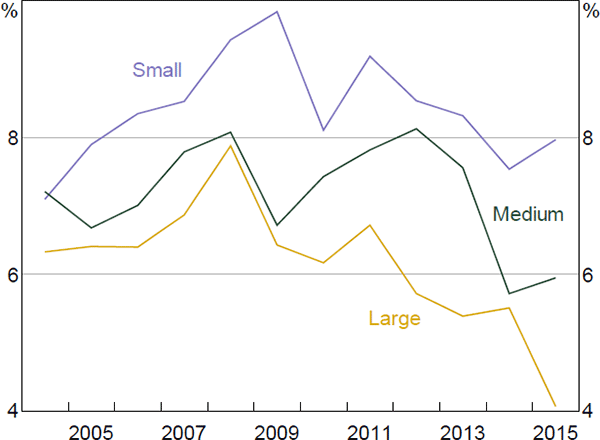
Notes: Size is based on total assets; small companies have assets below the median, medium companies are between the median and 75th percentile and large companies are above the 75th percentile
Sources: Authors' calculations; Company reports; Morningstar
Over recent years, the median borrowing rate for large companies (with assets greater than the 75th percentile) has declined substantially, to be at its lowest level in the sample period. The median rate paid by medium-sized companies (assets between the median and 75th percentile) has also declined, though to a lesser extent. In contrast, the median rate paid by small companies (with assets below the median) has been little changed since 2010 and remains near its decade-long average.[6] This suggests that declines in the cash rate in recent years have not necessarily flowed through to the interest rates faced by small companies.
We can also consider a more explicit measure of default risk. Distance to default (D2D) is a forward-looking market-based measure of default risk calculated using equity prices and the book value of liabilities.[7] A decline in D2D indicates deteriorating financial health and greater default risk. We classify companies with D2Ds below the 25th percentile as ‘more risky’ companies. All other companies are classified as ‘less risky’.
Similar to the trends based on company size, the median interest rate for the more risky companies is currently around its sample average, while, for less risky companies, it has declined substantially to be at its lowest level since 2004 (Figure 3). As a result, the spread between the median interest rate for more and less risky companies is elevated.
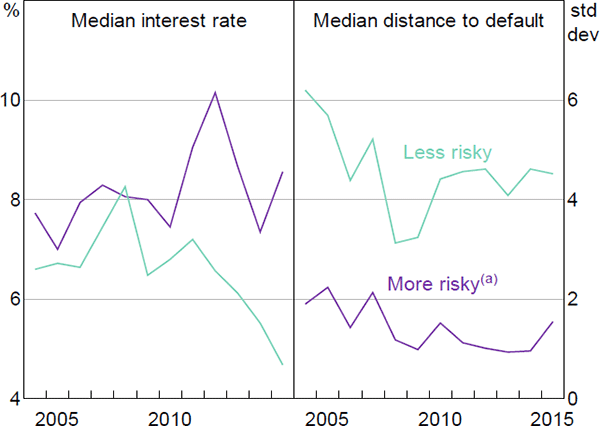
Note: (a) More risky companies are those with distance to default below the 25th percentile
Sources: Authors' calculations; Company reports; Morningstar; RBA
In part, the high level of the spread is likely to reflect an upward repricing of default risk following the financial crisis. It could also reflect the fact that the relative riskiness of the two groups has changed over recent years, with more risky companies becoming even more risky compared to other companies (Figure 3). Median D2Ds declined for both groups during the financial crisis; however, while the median D2D for less risky companies has trended higher since the crisis, the median D2D of more risky companies has remained at a low level.
2.3 The Cost of Equity
The focus in this paper is mainly on the cost of debt and its relationship with investment. However, for completeness, it is worth also considering what has happened to the cost of equity.
We consider two measures of the cost of equity, both of which are real, rather than nominal, measures. The first is analysts' forecasts for sectoral earning yields in one year's time (total earnings before interest and tax divided by market capitalisation; Figure 4). This is an ex ante measure of the required rate of return on equity, which makes it superior, at least conceptually, to ex post observed earnings yields used in previous studies such as La Cava (2005).
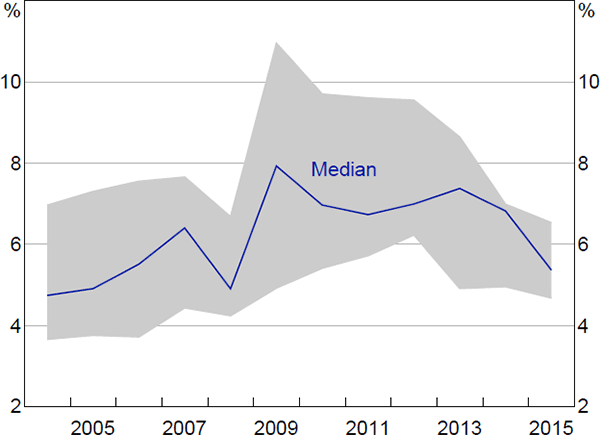
Note: Shading denotes range of yields
Source: Bloomberg
While there is a degree of heterogeneity, the costs of equity for all sectors have followed broadly similar paths. The cost of equity increased sharply around the financial crisis and remained high for several years, before returning to pre-crisis levels.
The second measure of the cost of equity is a company-specific rate estimated using a capital asset pricing model (CAPM). The CAPM states that:
where  is the cost of equity for company i at time t,
is the cost of equity for company i at time t, 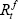 is the risk-free interest rate,
is the risk-free interest rate, 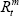 is the market rate of return and βi indicates the degree of co-movement between returns on the company's equity and the market portfolio (the degree of systematic risk).
is the market rate of return and βi indicates the degree of co-movement between returns on the company's equity and the market portfolio (the degree of systematic risk).
To estimate Equation (1) we need an observed ex post measure of the cost of equity. For this we use the share market return over a given period. We then assume this ex post return is an unbiased proxy for the ex ante cost of equity. This allows us to construct estimates of βi by running a regression at a monthly frequency for the full sample period (or the maximum possible sub-sample if the company was listed or delisted during the period). We take the return on the ASX 200 to be the market rate of return, and calculate both the return on the ASX 200 and on the individual company using accumulation indices that account for dividends, share issuance and share splits. Our risk-free rate is the average real cash rate expected over the next 10 years. The estimated β tend to be similar if we use short-term nominal rates instead.[8]
Many listed companies use the CAPM approach to estimate their cost of equity (Lane and Rosewall 2015). However, the cost of equity estimates are prone to model misspecification in the CAPM relationship. For example, the estimated β parameter is somewhat sensitive to the sample choice.
Note: Estimated using a company-specific CAPM model
The median of the company-specific cost of equity measures follows a similar path to the sectoral measures (Figure 5). Unsurprisingly, there is greater heterogeneity in the cost of equity based on the company-specific measure compared to the sectoral measure. The cost of equity for the 10th percentile remained relatively low during the crisis and has trended downwards over recent years. In contrast, the cost of equity for the 90th percentile increased by more during the crisis and remains at an elevated level.[9]
2.4 The Cost of Finance
For completeness, we also consider a more comprehensive measure of the ‘cost of finance’. This captures the fact that some companies rely on debt, some rely on equity and some rely on a combination of both. The cost of finance is measured as the weighted average of the costs of debt and equity. The weights on debt (D) and equity (E) are their respective shares in the total book value of the company. Specifically, the cost of finance is given by:
where 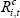 is the cost of finance for company i at time t,
is the cost of finance for company i at time t, 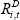 is the cost of debt, (1 – τt) accounts for the tax deductibility of interest payments,
is the cost of debt, (1 – τt) accounts for the tax deductibility of interest payments, 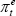 is expected inflation and
is expected inflation and 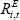 is the cost of equity.
is the cost of equity.
There is again a significant degree of heterogeneity across companies in the cost of finance, reflecting heterogeneity in both of the components. This additional detail is lost when focusing on aggregate measures, such as indicator lending rates.
2.5 Corporate Investment
We consider two different estimates of corporate investment:
- The net change in the fixed capital stock (‘net investment’);
- Cash spent on property, plant and equipment (‘gross investment’).
There are a few differences between these two estimates. The first estimate is an accrual-based measure of real net investment. It is an accrual-based measure because it recognises investment at the time the expense is incurred and not when the cash is spent. It is a real measure because the underlying capital stock is measured at replacement cost, using a method that accounts for changes in the price of capital goods (similar to Mills, Morling and Tease (1994) and La Cava (2005)). And it is a net measure because it excludes depreciation (i.e. spending to replace depreciated capital is not considered investment).[10]
The second estimate is a cash-based measure of nominal gross investment. It is a cash-based measure because it recognises investment at the time the cash is paid. It is a nominal measure because it does not allow for changes in capital goods prices (although the model specification will soak up aggregate changes in the relative price of capital goods). And it is a gross measure because it includes total spending on investment (i.e. does not exclude depreciation) and is therefore more aligned with aggregate investment indicators, such the ABS capital expenditure survey.
In both cases we focus on investment in tangible assets, such as property, plant and equipment, rather than investment in intangible assets, such as the accumulation of goodwill or investment in R&D. While a number of recent papers have demonstrated the importance of accounting for investment in intangibles when estimating investment regressions (e.g. Peters and Taylor 2016), limitations in our company balance sheet data make this difficult.
We scale both measures of investment by the previous period's capital stock, measured at the (real) replacement cost. Importantly, we trim the top and bottom 5 per cent of observations to remove extreme observations. This is fairly common practice in the investment literature using micro data (e.g. Bond and Van Reenen 2007). Given the initial small sample size, the results are a bit sensitive to the choice of trim. But the results are qualitatively similar if we, for example, trim the top and bottom 1 or 10 per cent.
Focusing on the median company, both gross and net investment follow similar paths and have been consistently lower after the financial crisis than before the crisis (Figure 6). This is consistent with aggregate measures of investment, and also with the overall cost of finance remaining elevated despite lower borrowing rates.[11]
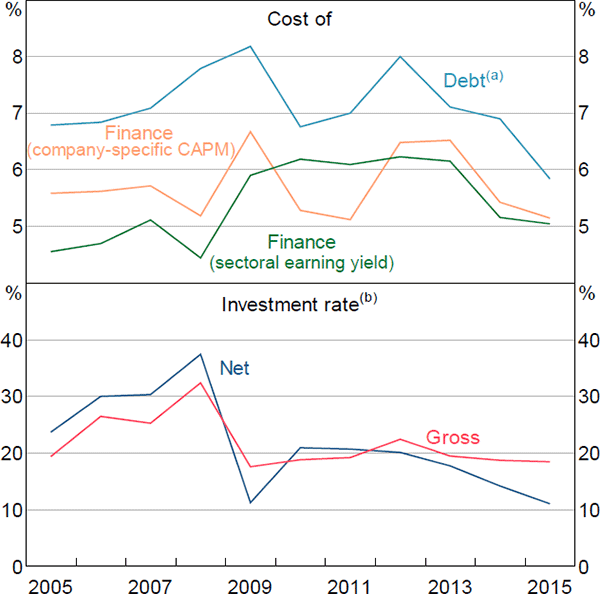
Notes:
(a) Collected borrowing rates
(b) Property, plant and equipment
Sources: Authors' calculations; Company reports; Morningstar
3. Reduced-form Model
3.1 Model Specification
Our reduced-form model specification is very similar to that in La Cava (2005). The model can be derived from a firm optimisation problem with a constant elasticity of substitution production function and adjustment costs (Bond and Van Reenen 2007). In the absence of adjustment costs, the company chooses an optimal level of real capital (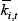 ) as a function of real sales (yi,t) and the real user cost of capital (uci,t), all measured in logs:
) as a function of real sales (yi,t) and the real user cost of capital (uci,t), all measured in logs:
where ai,t is an intercept that accounts for productivity shocks and σ is the elasticity of substitution between labour and capital. The user cost reflects the cost of investment, while the level of sales captures the company's investment ‘fundamentals’ (Gilchrist and Zakrajšek 2007).
Due to adjustment costs, the company's actual capital stock (ki,t) may diverge from the optimal capital stock. As such, there will be a long-run optimal level towards which the capital stock should adjust, as well as short-run dynamics (associated with the past values of capital, sales and the cost of capital). To account for this, Equation (3) can be nested in a general dynamic model which includes lags of independent and dependent variables:[12]
where ωi is a company fixed effect and τt is a year fixed effect. The company fixed effect captures time-invariant company-specific factors, such as their average productivity or business model. The time fixed effects capture aggregate influences, such as the business cycle, aggregate uncertainty and economy-wide changes in the relative price of capital goods.
This model can be re-parameterised as an error correction model (ECM), which allows for easy identification of the long- and short-run dynamics:
where 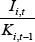 is the net investment rate, which is approximately the log change in the capital stock.
is the net investment rate, which is approximately the log change in the capital stock.
We are mainly interested in the coefficients on the cost of capital terms (i.e. γ0, γ1 and γ2). If these coefficients are estimated to be negative, it suggests that a lower cost of capital is associated with higher investment. Moreover, if γ2 is significant, and the speed of adjustment coefficient α2 is significantly negative, it suggests that there is a long-run inverse relationship between the cost of capital and the level of capital.
Fixed-effects estimation of Equation (5) is inconsistent due to the inclusion of a lagged dependent variable (which is correlated with the error term). As such, we estimate the model using the Arellano-Bond dynamic panel generalised method of moments (GMM) estimator (Arellano and Bond 1991).
For estimation, the model specification is adjusted slightly. First, the user cost of capital is replaced with either the cost of debt or the cost of finance.[13] The user cost of capital is a broader measure than the cost of debt or finance. It not only includes the cost of finance, but also includes a component to account for the tax treatment of revenue and depreciation, and a component to capture the relative price of capital goods. We focus on the cost of debt and finance as we want to specifically examine their relationship with investment, abstracting from these other factors.[14]
The second departure is that one of our investment measures is a gross measure, whereas the relationship in Equation (5) is derived for a net measure (change in the capital stock). While this should not introduce any estimation issues, the model is no longer an ECM as gross investment is not the change in the capital stock. Therefore, while we continue to use the same framework for ease of exposition, our focus is on the short-run relationship when using gross investment.
3.2 Results
3.2.1 Cost of debt
Table 1 contains the estimated coefficients using the cost of debt.
| Net investment | Gross investment | |
|---|---|---|
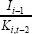 |
−0.52*** (0.14) |
−0.23** (0.10) |
| ki,t−2 | −0.63** (0.31) |
0.05 (0.14) |
| Cost of debt | ||
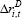 |
−0.47*** (0.14) |
−0.24** (0.12) |
 |
−0.63** (0.26) |
−0.31 (0.20) |
 |
−0.92** (0.43) |
−0.30 (0.33) |
| Sales | ||
| Δyi,t | 0.15*** (0.05) |
0.16*** (0.06) |
| Δyi,t−1 | −0.01 (0.09) |
−0.12 (0.07) |
| yi,t−2 | −0.15 (0.17) |
−0.18 (0.15) |
| Observations | 259 | 264 |
|
Notes: *, **, *** indicate significance at the 10, 5 and 1 per cent levels, respectively; standard errors are reported in parentheses and are robust to autocorrelation and heteroskedasticity; estimated using Arellano-Bond dynamic panel GMM estimator |
||
For net investment, a decrease in the cost of debt leads to higher investment in the short run and to a higher level of capital in the long run. This is shown by the coefficients on the interest rate terms. Both of these relationships are statistically significant.[15] To get a sense of the dynamics and the economic significance, Figure 7 shows the effect of a permanent 1 per cent decrease in the cost of debt on the rate of investment (confidence intervals are constructed using bootstrapping).[16] The lower cost of debt increases the investment rate by around ½ percentage point within two years, before its effect dissipates. Accordingly, the capital stock rises by around 1½ per cent. This implies that the elasticity of the capital stock with respect to the cost of debt is 1½. This is broadly consistent with estimates of the elasticity of the capital stock with respect to the user cost of capital for Australia (La Cava 2005), and for other small open economies such as Canada (Schaller 2006). Considering gross investment, there is again evidence consistent with a lower cost of debt being associated with higher investment. Overall, the results indicate that borrowing rates have a direct effect on the investment of indebted companies.[17]
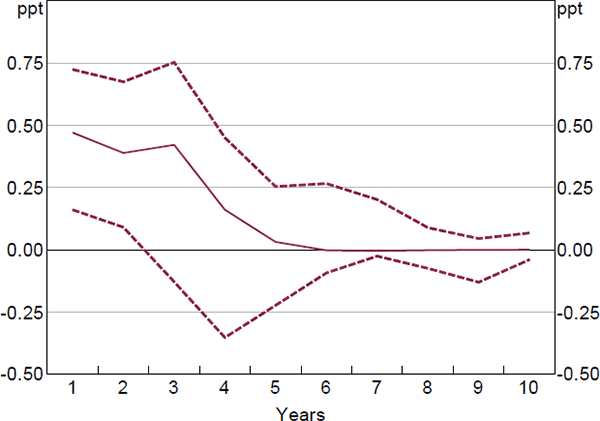
Notes: Model using net investment and the cost of debt; dashed lines are bootstrapped 90 per cent confidence intervals
As a robustness test, we also estimated the model treating sales and interest rates as predetermined variables, rather than as strictly exogenous variables. This involves using a reduced set of instruments for the GMM estimation. The results (not shown) are reasonably similar, and continue to show a negative relationship between investment and interest rates. We also found no evidence of serial correlation in the errors at an order above one in the main model, suggesting that the instruments are valid.[18]
Importantly, our results do not necessarily indicate why there is a link between interest rates and investment. For this, we would need to isolate a plausibly exogenous source of variation in interest rates, which is inherently difficult. But we can rule out some explanations. For example, the relationship does not appear to be due to monetary policy, at least not directly, as we control for aggregate business cycle variables through time fixed effects. And it does not appear to be due to company risk, as the results are nearly identical if we control for indicators such as D2D. Moreover, it does not appear to reflect the fact that sales are a backward-looking measure of demand, whereas interest rates and investment might be affected by the outlook for future sales, as the relationship still holds when we estimate a model including a forward-looking measure of demand: Tobin's q (see Appendix B).
Instead, we hypothesise that the inverse relationship between interest rates and investment is due to credit supply effects. A relaxation of lending standards leads to lower interest rate spreads (for a given company profile), which encourages more investment.[19] The relationship could also reflect differential timing in the repricing of debt, with some companies having to refinance during periods of high rates, such as the financial crisis, and others not. Those that do not have to refinance will face lower rates and so may invest more, all else equal. In many senses, this is quite similar to an idiosyncratic credit supply shock.
Consistent with La Cava (2005), the estimated coefficient on the lag of investment is negative and significant, indicating negative autocorrelation. So periods of high investment tend to be followed by periods of lower investment. This is at odds with models that incorporate convex adjustment costs in order to smooth investment over time (for a discussion, see Bond and Van Reenen (2007)); it is more consistent with companies investing in bursts, potentially due to the lumpy nature of larger projects (e.g. a new factory).
3.2.2 Cost of finance
Table 2 contains the estimated coefficients using the cost of finance. There is no evidence of a significant negative relationship between the cost of finance and investment using either gross or net investment, for either the sectoral or company-specific measures of the cost of equity.
The leading explanation for finding a significant negative relationship between investment and the cost of debt, but not the cost of finance, is that the cost of equity is poorly measured. This is not entirely surprising given that the cost of equity is unobserved and hard to measure. Companies have noted this as part of the RBA's business liaison programme (Lane and Rosewall 2015).[20]
An alternative explanation is the sample. When we switch from the cost of debt to the cost of finance the sample expands, as it now includes companies that have no debt (and as such have no borrowing rate data). If companies with no debt are less responsive to changes in the marginal costs of debt and finance – for example, because they are credit constrained – this could help to explain why the coefficients are no longer statistically significant. It would also suggest that our earlier findings for the cost of debt are subject to sample selection bias, and are only representative for the sub-sample of companies with debt.
| Company-specific | Sectoral | ||||
|---|---|---|---|---|---|
| Net investment | Gross investment | Net investment | Gross investment | ||
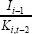 |
−0.22 (0.16) |
−0.74*** (0.08) |
0.11 (0.14) |
−0.66*** (0.14) |
|
| ki,t−2 | −0.25 (0.33) |
−0.49*** (0.15) |
0.31 (0.52) |
−0.62*** (0.27) |
|
| Cost of finance | |||||
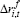 |
0.15 (0.10) |
0.01 (0.10) |
0.18 (0.32) |
0.03 (0.10) |
|
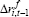 |
0.26 (0.28) |
0.23 (0.17) |
1.04 (0.94) |
0.41*** (0.14) |
|
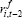 |
−0.32 (0.50) |
0.64*** (0.24) |
0.91 (1.39) |
0.77*** (0.26) |
|
| Sales | |||||
| Δyi,t | 0.13* (0.08) |
0.16*** (0.07) |
0.15** (0.07) |
0.12*** (0.03) |
|
| Δyi,t−1 | −0.02 (0.12) |
0.22*** (0.09) |
−0.61 (0.43) |
−0.01 (0.10) |
|
| yi,t−2 | −0.21 (0.20) |
0.55*** (0.18) |
−0.80* (0.48) |
0.20 (0.22) |
|
| Observations | 320 | 330 | 343 | 352 | |
|
Notes: *, **, *** indicate significance at the 10, 5 and 1 per cent levels, respectively; standard errors are reported in parentheses and are robust to autocorrelation and heteroskedasticity; estimated using Arellano-Bond dynamic panel GMM estimator |
|||||
One simple way to test whether the result is due to sampling is to estimate the cost of finance models over a reduced sample that only includes companies with debt. If the coefficients are different to those obtained by estimating the model over the full sample, it would suggest that companies with debt have a different elasticity of investment with respect to the cost of finance, and therefore potentially a different elasticity with respect to the cost of debt.
Estimating the model over the sub-sample of companies with debt leads to quite similar coefficients on the cost of finance (not shown). This suggests that our results for the cost of debt are not materially affected by any sample selection biases. We examine this further below.
4. Accounting for Sample Selection
Our estimates of the sensitivity (or ‘elasticity’) of company investment with respect to the cost of debt may be affected by sample selection bias. Interest rate data are only observable for companies with debt; therefore, we can only estimate the elasticity for these companies. If companies without debt have a different elasticity, our estimates will be biased.
It is difficult to assess the size and direction of this bias. We could be overestimating the size of the negative relationship between interest rates and investment if companies with debt are relatively more sensitive to interest rates. This might be the case if, for instance, companies that have outstanding floating-rate debt receive higher cash flows when rates fall, which could stimulate investment if they are financially constrained (e.g. Ippolito, Ozdagli and Perez-Orive 2017). Companies without debt would not be affected by this cash flow channel, and so would be less sensitive to interest rate changes. Alternatively, we could be underestimating the negative relationship between interest rates and investment if companies without debt are more sensitive to interest rates. This might happen if there are companies that have no debt because they are borrowing constrained, and for whom the constraint would be relaxed if rates fell and made serviceability more feasible.[21] A slight fall in rates would lead to a large increase in borrowing and investment by these companies.
The standard approach to dealing with sample selection bias is to use a sample selection model, such as the Heckman (1979) approach, or an endogenous switching model (e.g. Lee 1978; Hu and Schiantarelli 1998). These approaches formally model the selection mechanism alongside the equation of interest. However, they are designed for cases where we are missing data on the dependent variable – investment – rather than on the explanatory variable – the interest rate – as these approaches generally include the explanatory variable in the selection model.
Instead, we employ multiple imputation (MI), a technique pioneered in Rubin (1987).[22] The idea behind MI is to impute reasonable values for the missing variables using the observed data and an imputation model. The imputed values can be used to complete the sample. The relationships of interest can then be estimated using the completed sample. Rather than doing this once, we do it multiple (m) times, and each time we add some random variation to the imputed variables. This allows us to account for noise and uncertainty in the imputation process. The coefficients of interest are taken as the average coefficient across the m estimations. The standard errors can be computed based on the variance of the coefficients within and between the m estimations.
For this approach to be valid, we need to assume that the data are ‘missing at random’ (MAR). That is, conditional on all of the other variables, the fact that the data are missing provides no additional information. To make this more concrete, in our case MAR requires that the missing nature of the interest rate data is not a signal that it is high (or low), once we take account of all of the information contained in the variables we have used to impute the interest rate. Put another way, the true missing observation should be equal to the imputed value plus a white noise error term.
In reality, this is likely to be a strong assumption. Under our maintained hypothesis, as interest rates increase, all else equal, companies are less likely to borrow, and so are more likely to be missing data. Our imputed interest rates are therefore likely to be lower compared to the true data. This ‘level’ effect can be dealt with relatively easily using company fixed effects.
More concerning is the possibility that the error is not white noise, and might be systematically related to investment. For instance, even if our imputation model is good, unobserved credit supply shocks will create a wedge between the imputed and true interest rate values. Therefore, the imputed interest rate variable will include an error that, under the maintained hypothesis, is positively correlated with investment. This means that our estimated coefficient is likely to be biased upwards.[23] Still, this at least allows us to say something about the likely direction of the bias, which we cannot do with the estimates from Section 3.2.1.
4.1 Model and Results
As noted above, to use MI we need to specify a model for imputation. We model interest rates as:
where Zi,t is a vector of variables taken from the company's balance sheet that may be related to the company's riskiness, demand for credit, and interest rates more generally.[24]
Table 3 contains the results from the MI estimation. The estimated coefficients on the cost of debt are negative, but are insignificant and are somewhat closer to zero than those we obtain when estimating the model using only companies with debt. This suggests that the companies without debt may have less interest-sensitive investment, compared to companies with debt. If this is the case, care needs to be taken in extrapolating results from regressions using only companies with debt to the whole universe of firms.
There are some caveats to this finding. First, as discussed above, the estimates are likely to be biased upwards. Therefore we cannot conclusively contend that the companies without debt have a lower elasticity of investment with respect to debt. Second, even if bias is not an issue, it is possible that the differences in elasticities could reflect our focus on tangible investment. In our sample, companies without debt appear to invest more heavily in intangible assets. This is consistent with the fact that many debt-free companies are in the healthcare and information technology sectors. As such, their tangible investment elasticity could be lower, but their total investment elasticity may not be.
Still, the potential for different elasticities of investment has important implications for understanding the pass-through of monetary policy and of shocks to the financial sector. As such, it would be worthwhile further interrogating the results in future work using other data sources or techniques.
| Net investment | Gross investment | |
|---|---|---|
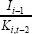 |
0.06* (0.03) |
−0.60** (0.05) |
| ki,t−2 | 0.04 (0.21) |
−1.58* (0.95) |
| Cost of debt | ||
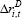 |
−0.22 (0.20) |
−0.20 (0.44) |
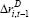 |
−0.20 (0.36) |
−0.35 (0.74) |
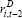 |
−0.38 (0.55) |
−0.83 (1.07) |
| Sales | ||
| Δyi,t | 0.20*** (0.05) |
−0.40 (0.48) |
| Δyi,t−1 | −0.07 (0.14) |
−0.83 (0.79) |
| yi,t−2 | −0.22 (0.22) |
0.11 (0.26) |
| Observations | 427 | 444 |
|
Notes: *, **, *** indicate significance at the 10, 5 and 1 per cent levels, respectively; standard errors are reported in parentheses |
||
5. Conclusion
Investment and the cost of debt are very heterogeneous across companies; at any point in time, some companies are investing while others are not. And, for those that are investing, they all face different interest rates. This paper highlights the importance of accounting for this heterogeneity when analysing the relationship between the cost of finance and investment. We document that the interest rates faced by some companies have remained relatively high in recent years. Moreover, we show that there is a significant negative relationship between company-specific interest rates and their investment, a relationship which is hard to establish with aggregate time-series data.
These findings have important implications for monetary policy. In particular, the low level of both the cash rate and average business lending rates may not have translated to lower borrowing rates for all companies. This may help to explain some of the weakness in non-mining business investment in recent years.
There are a few caveats to our analysis. First, it is unclear whether our results generalise beyond a sample of listed companies with debt to the broader corporate population. Multiple imputation techniques suggest that the relationship may be weaker for companies without debt and that other studies fail to properly account for sample selection when focusing purely on firms with debt.
Second, our results do not establish why there is a link between interest rates and investment as we do not isolate a plausibly exogenous source of variation in interest rates. The negative relationship between interest rates and investment does not appear to reflect changes in monetary policy, at least not directly, as we control for aggregate fluctuations in the analysis. The relationship is also not due to variation in company risk, as this is controlled for through various indicators such as the distance to default. Instead, we argue that it may be due to credit supply effects. A relaxation of lending standards leads to lower interest rates (for a given company profile), which encourages more investment.
Appendix A: Summary Statistics
Table A1 displays median assets and gearing for our sample, along with the ‘population’ counterparts based on all listed companies contained in the Morningstar database (excluding companies in the financial and resource-related sectors).
| Assets ($m) | Gearing (%) | ||||
|---|---|---|---|---|---|
| Sample | Morningstar(a) | Sample | Morningstar(a) | ||
| 2004 | 28.6 | 36.7 | 26.7 | 38.5 | |
| 2005 | 36.7 | 41.6 | 29.9 | 42.6 | |
| 2006 | 39.6 | 44.7 | 35.5 | 45.8 | |
| 2007 | 41.8 | 45.5 | 39.0 | 48.7 | |
| 2008 | 39.2 | 48.5 | 46.8 | 55.1 | |
| 2009 | 44.8 | 45.7 | 46.5 | 47.4 | |
| 2010 | 41.9 | 43.3 | 42.5 | 42.7 | |
| 2011 | 57.7 | 38.6 | 35.6 | 42.2 | |
| 2012 | 52.5 | 34.0 | 39.3 | 42.4 | |
| 2013 | 49.5 | 39.6 | 42.2 | 40.9 | |
| 2014 | 58.0 | 41.0 | 39.6 | 37.2 | |
| 2015 | 54.8 | 44.1 | 25.7 | 37.8 | |
|
Note: (a) Excludes financial and resource companies Sources: Authors' calculations; Morningstar |
|||||
Appendix B: Tobin's q Models
The use of company-level data helps to ameliorate endogeneity that arises from the mismeasurement of aggregate economic investment fundamentals, as we can use time effects to capture these fundamentals. However, we may be mismeasuring company-level investment fundamentals if company sales are a poor indicator of fundamentals. This could lead to other sources of endogeneity. For example, improvements in the outlook for future growth could lead to more investment. At the same time, the company's risk of default, and therefore its cost of debt and finance, is likely to fall. Current sales will be unaffected. This would cause our estimates of the effect of the cost of debt and finance on investment to be negatively biased, meaning our results would be overstated. Alternatively, if investment increases the company's risk of default and therefore funding costs, this would lead to a positive bias in our estimates and suggest our estimated relationships are understated.
To better capture these dynamics, we estimate a second model that incorporates company fundamentals in a different way. It includes two measures of company fundamentals. One is Tobin's average q, which measures the ratio of the average value of capital inside and outside the company. Under certain assumptions, the average q is equivalent to the marginal q – the ratio of the marginal value of an additional dollar of capital inside and outside of the company – which is the fundamental driver of investment according to the q theory of investment (Hayashi 1982).[25] If the value of capital is higher inside the company, the company should invest; if the value is higher outside, it should disinvest and return money to shareholders.
We construct our measure of the average q as:
where the market value of equity is calculated by multiplying the outstanding number of ordinary shares by the closing stock price at the end of the financial year.
Technically, the denominator of the average q should be the replacement value of the capital stock, rather than the book value of the assets. However, using the replacement value leads to a number of complications. In particular, companies' equity and debt fund a large number of non-capital assets, including financial instruments and other investments, and the ratio needs to be adjusted for these or else it will be systematically overstated. This adjustment is difficult and imprecise due to data limitations, and due to the accounting treatments of investments and intangibles. Instead, we use this simpler measure of q, which is very similar to the measure adopted in Gutiérrez and Philippon (2016). More broadly, even if the measure cannot be thought of strictly as a measure of q, it may still be useful as it provides a forward-looking indicator of the company's investment opportunities given it includes the market value of equity (Caballero 1999).[26]
Similar to Gilchrist and Zakrajšek (2007), we also attempt to account more directly for company default risk by including a measure of default risk (D2D). Again, D2D does not have a direct role in q-type models and should, in theory, be captured by the average q measure. However, given the already discussed difficulties in accurately measuring q, we incorporate D2D into the analysis.
We estimate the following simple model:
We use the change in the cost of debt or finance to be more consistent with the model outlined in Section 3. According to theory, the capital stock is a function of the level of the user cost of capital. Therefore, investment, which is the change in the capital stock, should be related to the change in the user cost of capital. In contrast to Section 3, we only include the contemporaneous change for simplicity, but the results are robust to including more lags.
Table B1 contains the results using the cost of debt in the Tobin's q model. For both the net and gross investment measures, the coefficients on the cost of debt are negative and significant. This provides additional support for our earlier findings regarding the relationship between investment and the cost of debt. The magnitudes are economically significant, though appear a bit smaller than those obtained in Section 3. A 1 per cent decrease in the cost of debt is associated with a ¼ percentage point rise in the investment rate.[27]
| Net investment | Gross investment | |
|---|---|---|
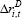 |
−0.25*** (0.10) |
−0.16*** (0.06) |
| qi,t−1 | 0.26*** (0.04) |
0.08** (0.03) |
| D2Dt−1 | −0.03*** (0.01) |
0.00 (0.00) |
| Observations | 375 | 385 |
|
Notes: *, **, *** indicate significance at the 10, 5 and 1 per cent levels, respectively; standard errors are reported in parentheses and are robust to autocorrelation and heteroskedasticity |
||
Moreover, the coefficient on q is positive and significant. It is also somewhat larger than what is found in earlier Australian studies such as Mills et al (1994) and La Cava (2005), and in the literature more broadly. Nevertheless, it is broadly in line with the estimates from Gutiérrez and Philippon (2016) for the United States.
Somewhat surprisingly, there is evidence of a negative relationship between D2D and investment. That is, as companies become more risky they invest more. One explanation could be that there is a degree of reverse causality: the act of investing makes companies more risky. However, it is difficult to draw too strong a conclusion without a proper structural model, which is beyond the scope of this paper.
Appendix C: Multiple Imputation Model References
As noted above, to use MI we need to specify a model for imputation. We model interest rates as:
where Zi,t is a vector of variables taken from the company's balance sheet that may be related to its riskiness, demand for credit, and interest rates more generally. These variables include: assets; the return on assets; the debt-to-assets ratio; the liquidity ratio (the ratio of cash to current liabilities); years since listing (in levels and squared terms); Tobin's average q; D2D. It also includes a number of indicators that take on the value one if: the company's D2D was in the bottom quartile; the company made a loss in the year; the company had negative equity; the company delisted within the next two years; the company was small (assets below the median); or if the company was of medium size (assets between the median and the 75th percentile). The coefficients on the variables in Zi,t are allowed to vary over time.[28]
A common approach is to use the output from the linear regression plus some random noise as the imputed values. The method is parametric, as the errors are assumed to be normally distributed when the noise is added. Instead, we use a method called predictive mean matching (PMM), first suggested in Little (1988). This is a semi-parametric approach that tends to be more robust than the fully parametric approach if the imputation model is misspecified (e.g. Schenker and Taylor 1996). Given the relationship between interest rates and the variables in Zi,t is likely to be highly nonlinear, we prefer this more robust approach.[29]
PMM uses a parametric linear regression, followed by a non-parametric nearest-neighbour regression. More formally, PMM involves six steps:
-
The imputation model is estimated using the complete data, yielding coefficients
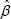 .
.
-
Coefficients β* are drawn from the posterior distribution of
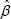 (assuming the errors are normally distributed).
(assuming the errors are normally distributed).
-
Values are imputed for the missing observations
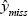 using β*.
using β*.
-
Values are imputed for the complete observation
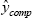 using β*.
using β*.
-
For each
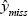 , we identify the k closest completed observations based on their imputed values
, we identify the k closest completed observations based on their imputed values 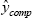 .
.
- We randomly choose one of these k completed observations, and use its true observed value ycomp as the actual imputed value ymiss.
The collection of ycomp and ymss can then be used to estimate the relationship of interest.
The choice of k represents a trade-off between efficiency and bias (similar to the choice of bandwidth in a kernel regression). Choosing k to be too low can lead to a loss of efficiency, as the imputed value for each observation can vary wildly between iterations. Choosing k to be too high could induce bias into the estimation, particularly if the observations are sparse. We set k = 3, which is relatively common in the literature. The results appear to be reasonably robust to the choice of k. We run the imputation and estimation 100 times. This is higher than the minimum number of iterations recommended in papers such as Bodner (2008).
References
Abel AB and JC Eberly (2004), ‘Q Theory Without Adjustment Costs & Cash Flow Effects Without Financing Constraints’, Paper presented at the Society for Economic Dynamics 2004 Annual Meeting, 1–3 July, Florence.
Arellano M and S Bond (1991), ‘Some Tests of Specification for Panel Data: Monte Carlo Evidence and an Application to Employment Equations’, The Review of Economic Studies, 58(2), pp 277–297.
Ashenfelter O and A Krueger (1994), ‘Estimates of the Economic Return to Schooling from a New Sample of Twins’, The American Economic Review, 84(5), pp 1157–1173.
Blanchard OJ (1986), ‘Comments and Discussion on “Investment, Output, and the Cost of Capital”’, Brookings Papers on Economic Activity, 1986(1), pp 153–158.
Blanchard OJ (2017), Macroeconomics, 7th edn, Pearson, Boston.
Bodner TE (2008), ‘What Improves with Increased Missing Data Imputations?’, Structural Equation Modeling: A Multidisciplinary Journal, 15(4), pp 651–675.
Bond S and J Van Reenen (2007), ‘Microeconometric Models of Investment and Employment’, in JJ Heckman and EE Leamer (eds), Handbook of Econometrics: Volume 6A, Handbooks in Economics 2, Elsevier Science, Amsterdam, pp 4417–4498.
Caballero RJ (1999), ‘Aggregate Investment’, in JB Taylor and M Woodford (eds), Handbook of Macroeconomics: Volume 1B, Handbooks in Economics 15, Elsevier Science, Amsterdam, pp 813–862.
Chirinko RS (1993), ‘Business Fixed Investment Spending: Modeling Strategies, Empirical Results, and Policy Implications’, Journal of Economic Literature, 31(4), pp 1875–1911.
Cockerell L and S Pennings (2007), ‘Private Business Investment in Australia’, RBA Research Discussion Paper No 2007-09.
Dunne T, MJ Roberts and L Samuelson (1988), ‘Patterns of Firm Entry and Exit in U.S. Manufacturing Industries’, The RAND Journal of Econometrics, 19(4), pp 495–515.
Enders CK (2010), Applied Missing Data Analysis, Methodology in the Social Sciences, The Guilford Press, New York.
Gilchrist S and E Zakrajšek (2007), ‘Investment and the Cost of Capital: New Evidence from the Corporate Bond Market’, NBER Working Paper No 13174.
Gutiérrez G and T Philippon (2016), ‘Investment-Less Growth: An Empirical Investigation’, NBER Working Paper No 22897, rev January 2017.
Hambur J and R Finlay (2018), ‘Affine Endeavour: Estimating a Joint Model of the Nominal and Real Term Structures of Interest Rates in Australia’, RBA Research Discussion Paper No 2018-02.
Hassett KA and RG Hubbard (2002), ‘Tax Policy and Business Investment’, in AJ Auerbach and M Feldstein (eds), Handbook of Public Economics: Volume 3, Handbooks in Economics 4, Elsevier Science, Amsterdam, pp 1293–1343.
Hayashi F (1982), ‘Tobin's Marginal q and Average q: A Neoclassical Interpretation’, Econometrica, 50(1), pp 213–224.
Heckman JJ (1979), ‘Sample Selection Bias as a Specification Error’, Econometrica, 47(1), pp 153–161.
Hsiao C (2003), Analysis of Panel Data, 2nd edn, Econometric Society Monographs No 34, Cambridge University Press, Cambridge.
Hu X and F Schiantarelli (1998), ‘Investment and Capital Market Imperfections: A Switching Regression Approach Using U.S. Firm Panel Data’, The Review of Economics and Statistics, 80(3), pp 466–479.
Ippolito F, AK Ozdagli and A Perez-Orive (2017), ‘The Transmission of Monetary Policy through Bank Lending: The Floating Rate Channel’, Board of Governors of the Federal Reserve System Finance and Economics Discussion Series No 2017-026.
Kenney R, G La Cava and D Rodgers (2016), ‘Why Do Companies Fail?’, RBA Research Discussion Paper No 2016-09.
La Cava G (2005), ‘Financial Constraints, the User Cost of Capital and Corporate Investment in Australia’, RBA Research Discussion Paper No 2005-12.
Lane K and T Rosewall (2015), ‘Firms' Investment Decisions and Interest Rates’, RBA Bulletin, June, pp 1–7.
Lee L-F (1978), ‘Unionism and Wage Rates: A Simultaneous Equations Model with Qualitative and Limited Dependent Variables’, International Economic Review, 19(2), pp 415–433.
Little RJA (1988), ‘Missing-Data Adjustments in Large Surveys’, Journal of Business & Economic Statistics, 6(3), pp 287–296.
Mankiw NG (2007), Principles of Economics, 4th edn, Thomson South-Western, Mason.
Mills K, S Morling and W Tease (1994), ‘The Influence of Financial Factors on Corporate Investment’, RBA Research Discussion Paper No 9402.
Moons KGM, RART Donders, T Stijnen and FE Harrel Jr (2006), ‘Using the Outcome for Imputation of Missing Predictor Values was Preferred’, Journal of Clinical Epidemiology, 59(10), pp 1092–1101.
Peters RH and LA Taylor (2016), ‘Intangible Capital and the Investment-q Relation’, Journal of Financial Economics, 123(2), pp 251–272.
Robson M (2015), ‘Default Risk Among Australian Listed Corporations’, RBA Bulletin, September, pp 47–54.
Rubin DB (1987), Multiple Imputation for Nonresponse in Surveys, John Wiley & Sons, New York.
Schaller H (2006), ‘Estimating the Long-Run User Cost Elasticity’, Journal of Monetary Economics, 53(4), pp 725–736.
Schenker N and JMG Taylor (1996), ‘Partially Parametric Techniques for Multiple Imputation’, Computational Statistics & Data Analysis, 22(4), pp 425–446.
Sharpe SA and GA Suarez (2014), ‘Why Isn't Investment More Sensitive to Interest Rates: Evidence from Surveys’, Board of Governors of the Federal Reserve System Finance and Economics Discussion Series No 2014-002, rev August 2015.
Footnotes
Specifically, companies are required to be listed on the stock exchange in 2007/08. This date was chosen to ensure we captured fluctuations in investment and interest rates around the time of the financial crisis. Within the 2007/08 listed company population, 100 companies were selected using a random number generator. [1]
The investment of listed companies may be more sensitive to interest rates than that of other firms if unlisted companies are totally excluded from the debt market (i.e. cannot borrow). But, in this case, the cost of equity should be important and we control for this in the analysis. [2]
There are differences in the way these two things are measured. For example, the ABS capital expenditure survey excludes land and second-hand asset purchases from capital spending. These are included in the company-level estimates. [3]
This is a nominal interest rate, whereas theory would suggest the real interest rate should be the more relevant determinant of investment. The results are robust to using a more complete real cost of debt measure that accounts for taxes and expected inflation. However, we do not use this in the main specification as the calculated real rates are negative for some observations. As we use log interest rates in the model these observations have to be discarded, which is not ideal given the already small sample. [4]
As well as the characteristics of the borrower, the characteristics of the loan are also likely to influence measured interest rates. Such characteristics might include: the term of the borrowing; the type of borrowing (e.g. bank loans and corporate bonds); the extent of collateralisation; or whether the company has existing relationships its lenders. While some companies do report this information, it is too sparse to be useful for analysis. [5]
We classify companies with assets below the median as ‘small’ to imperfectly account for the roughly log-normal distribution of company assets – the company with median assets (around $40–50 million) is much closer in size to the company at the 25th percentile of the asset distribution (around $10 million) than it is to the company at the 75th percentile (around $200–250 million). [6]
The median D2D for companies in our sample is broadly consistent with the median D2D for all non-financial listed companies. The D2D measure is the difference between the expected value of assets and the expected value of liabilities at a chosen horizon (one year in this paper) and is measured in standard deviations of asset value growth. For more information, see Robson (2015). [7]
We construct this measure using the term structure model laid out in Hambur and Finlay (2018). [8]
For some sectors, such as utilities and consumer discretionary, the median company-specific cost of equity follows the sectoral cost of equity quite closely. For others, such as consumer staples, it does not. [9]
A problem with the net investment measure is that it can be affected by mergers, acquisitions and sales of business divisions. Ideally, we would abstract from these transactions as they do not really reflect the creation or destruction of capital in the economy and could be driven by very different factors to capital spending. While we do not directly observe these transactions, we control for some of them by deleting outliers from the distribution. [10]
A fall in the median gearing ratio amongst the sample could help to account for the fact that the median cost of finance has remained elevated despite declines in the median cost of debt. [11]
The choice to include two lags is somewhat arbitrary. However, given the data are annual and the sample is relatively short, using longer lag specifications will likely lead to less precise estimates. [12]
We take the rate payable at the end of the financial year to be the marginal rate the company faces over the next year. For example, if a company's average interest rate payable on debt as at 30 June 2005 is 5 per cent, we take 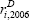 to be 5 per cent.
[13]
to be 5 per cent.
[13]
The relationship in Equation (5) is for the cost of capital, but excluding components such as the relative price of capital goods should not introduce any particular biases. Such components are generally measured at an aggregate or sectoral level and are additively separable when the user cost of capital is defined in logs. As such, they should be relatively well captured by the company and time fixed effects. Even if they are not well captured, their exclusion should not pose major problems as there is unlikely to be much correlation between these aggregated measures and the company-specific measures of the cost of finance. Moreover, leaving these components out of the long-run relationship should not lead to any estimation issues, even if the variables are non-stationary. In a time-series regression, if the variables were non-stationary we would need to have a properly specified cointegrating relationship to ensure that the errors are stationary, or else inference would be invalid. However, this is less of a concern in a panel regression, particularly if the panel is made up of a short time series and large cross-section, as is the case here (e.g. Hsiao 2003). Still, it does suggest some caution in interpreting any long-run relationships. [14]
We considered examining whether the elasticities differed for companies of different sizes or risk profiles, but the sample was too small. [15]
Instead of sampling individual company-year observations with replacement, we sample companies. This maintains the dependence structure within the data. We bootstrap 1,000 times. [16]
The results are robust to including cash flow (as measured by the ratio of earnings before interest, tax, depreciation and amortisation to total assets) in the model. [17]
An alternative test is the Sargan test of over-identifying restrictions, but this tends to perform relatively poorly in the presence of heteroskedasticity (Arellano and Bond 1991). [18]
The relationship may also reflect variation in the mix of debt instruments held by companies. The companies facing higher interest rates could be relying on more expensive forms of borrowing, such as credit cards or overdrafts, rather than bank loans or corporate bonds. Our estimates combine these debt instruments. It may be that companies shift towards cheaper borrowing instruments when they invest. Though, as we use interest rates as at the beginning of the year, it is unlikely that such behaviour is materially affecting our results. [19]
We experimented with using one noisy measure of the cost of finance as an instrument for the other in the vein of Ashenfelter and Krueger (1994). While there is slightly more evidence of a negative relationship between the cost of finance and investment the results were still not significant. Moreover, the cost of finance measures appear to be relatively weak instruments for each other. [20]
This might happen if, for example, there is some fixed cost in making initial debt offerings, or in forming a relationship with a bank and getting an initial loan. [21]
For an overview of MI as well as other methods to deal with missing data, see Enders (2010). [22]
To get around this issue most of the literature recommends including the outcome variable in the imputation equation. This would seem to lead to ‘self-fulfilling prophecies’ where we find a relationship between the imputed and outcome variables by construction, but a number of papers have shown that this is not the case (e.g. Moons et al 2006). However, our study differs somewhat from most of the literature in that we are specifically concerned that those companies with missing data may have a different relationship between the explanatory variable and the outcome variable. [23]
For more details on the actual estimation, see Appendix C. [24]
In Abel and Eberly (2004), it is actually the average q, not the marginal q that is relevant for investment. [25]
This type of interpretation is more in line with the model in Abel and Eberly (2004), where investment is related to average q because average q provides information on future profits. [26]
The results are robust to including cash flow in the equation. [27]
Pooling the β for the full sample does not affect the results. Neither does modelling interest rates in log levels. [28]
We experimented with using the linear regression approach. The results were broadly similar, though the imputed interest rates were unreasonable in some cases. [29]