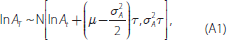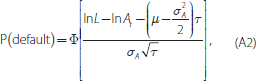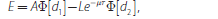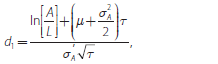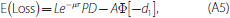Bulletin – September 2015 Financial Stability Default Risk Among Australian Listed Corporations
- Download the article 334KB
Abstract
Market-based information can help detect deteriorating corporate health because it incorporates more forward-looking information than other data sources such as financial statements. With this in mind, the Reserve Bank has developed an indicator of financial health based on a contingent claims framework developed by Merton (1974), which is sometimes called a distance-to-default model. The Bank will primarily use the model to assess trends in financial health for the corporate sector as a whole and, in aggregate, the model is able to broadly match the dynamics of the corporate failures data, suggesting that it will be a useful addition to the Bank's existing suite of monitoring tools. The results from the model suggest that corporate financial conditions remain robust, despite some deterioration more recently, which partly reflects the headwinds faced by listed resource companies.
Introduction
Historically, businesses have accounted for a disproportionate share of the non-performing loans, and ultimately the losses of banks both in Australia and overseas (Rodgers 2015). There are a number of reasons why business lending is inherently riskier than household lending: limited liability structure, competitive pressures and their more direct exposure to cyclical fluctuations in activity. These heighten the risk of default for individual businesses and lead to common vulnerabilities at both the industry level and for the business sector as a whole. The resulting correlation in business sector defaults, in combination with the fact that business loans are less likely than housing loans to be backed by high-quality collateral, means that, on average, deterioration in the financial health of businesses is more likely to transmute into a threat to financial stability.
The Bank's regular monitoring currently focuses on the listed corporate sector, primarily because of data limitations but also because listed corporations are on average larger and more likely to contribute directly to a systemic shock. Financial statements are the main source of information about corporate health used in the Bank's monitoring, supplemented with market-based information, such as equity prices. However, a strand of the existing literature on corporate credit risk suggests that combining the two types of information detects deteriorating corporate health more effectively than either source alone (see, for example, Hillegeist et al (2004)).
With this in mind, the Bank has developed an indicator of financial health based on a contingent claims framework developed by Merton (1974), sometimes called a distance-to-default (D2D) model. The indicator uses information on liabilities from financial statements together with a company's market capitalisation to assess credit risk. Individual companies' probabilities of default can be aggregated to assess risk for particular industries or for the business sector as a whole. The key simplifying assumption underpinning the model is that a company will default if the market value of its assets falls below the book value of its liabilities. The difference between the value of assets and liabilities determines the company's probability of default (PD).
Variants of the Merton model are widely used in commercial and policy-making settings; the level of focus – such as on sectoral trends versus individual corporations – varies widely in application. The most prominent commercial application of the D2D model is by Moody's KMV in its Expected Default Frequency (EDFTM) product (see Crosbie and Bohn (2003) for a description of the model). This is a more complex model using an option pricing framework that can accommodate multiple classes of liabilities. It uses a proprietary database of corporate defaults, which allows for an empirical mapping from the D2D to the PD (rather than mapping via a normal distribution that has some limitations).
In the regulatory sphere, the International Monetary Fund and the Bank of England have used the Merton approach to assess the vulnerability of non-financial companies, with some success in determining which companies are most likely to default (Tudela and Young 2003; IMF 2009). Similar models have also been applied to the banking sector: Gizycki and Goldsworthy (1999) present an earlier application at the Bank, while the Danmarks Nationalbank (2009) uses a Merton model to examine the risk of financial institutions breaching regulatory capital ratios. More recently, D2D models have been used in efforts to uncover ongoing vulnerabilities in euro area banks (Saldias 2012) and to assess the effectiveness of the Basel II framework (Blundell-Wignall and Roulet 2012).
The Merton Model
The basic Merton model produces an estimate of the PD for a listed company based on its market valuation and its outstanding liabilities by making an assumption about the evolution of the value of its assets. The model assumes a simple financial structure, comprising a single senior debt claim and a junior equity claim. Under these assumptions, a firm defaults when the market value of its assets falls below the value of its liabilities. As information on liabilities is limited to semi-annual financial statements, the model assumes that liabilities are constant over the horizon of interest, in this case one year. To determine the probability of default, only the value of assets needs to be determined. Asset values are assumed to drift higher at the risk-free rate over time, with random shocks driving variation around this assumed path. As a result, the range of possible asset values in the future may be sufficiently wide to include asset values that are lower than the fixed value of liabilities, in which case the company will be in default. The range of potential asset values at the 12-month horizon is represented by a probability distribution function; in this case returns are assumed to be log-normally distributed.[1] The PD can be thought of as the area under the portion of the distribution function that is below the value of liabilities (sometimes called the default point or the debt barrier). Alternatively, the expected gap between asset and liability values can be standardised and expressed in terms of the asset return volatility, which is the D2D.
If the market value of assets was observable, the model would be simple to implement. However, the market value of assets cannot be observed directly. Merton's insight was that, in the framework described above, the position of the holders of the equity claim on the corporation is equivalent to their possessing a call option on the company, where the strike price is the value of its liabilities. If the value of assets exceeds the value of liabilities when debts mature, the debts are paid and the equity holders keep any excess value. However, if the market value of assets falls below the value of liabilities, there is no incentive to pay back the debt; on the contrary, it makes sense to forfeit the equity value and default. Accordingly, option pricing theory can be used to derive the market value and volatility of assets from the value and volatility of equity and the value of liabilities. The key expressions that define the model are outlined in Appendix A.[2]
Results
While commercial variants of the Merton model are designed to maximise the accuracy of assessments of the financial health of individual companies, the Bank will primarily use the model to assess trends in financial health for the corporate sector as a whole. Tracking developments in the distribution of the D2D or PD, as shown in Graphs 1 and 2, is one way to monitor aggregate developments.[3] Looking at the historical trends in the D2D, the period around the 2008 crisis stands out (as expected), with the combination of falling equity prices and heightened volatility driving the median D2D to a trough of around 2½ standard deviations. Across the distribution there is a common pattern of the D2D rising to a relatively high level in the early 2000s, before peaking around the middle of the decade and then falling sharply over 2007–08. The subsequent recovery reflected a combination of rebounding equity prices, diminished volatility and declining leverage, with the median D2D peaking in mid 2014 at around its pre-crisis high.[4] The recent sharp fall in the D2D partly reflects weakness in the resource sector, consistent with falling commodity prices.
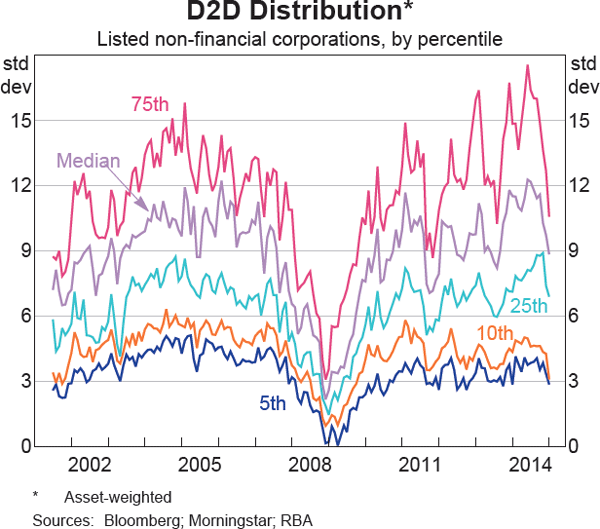
While the D2D is easy to interpret in a qualitative sense – a lower D2D equates to a deterioration in financial health – the fact that it is expressed in standard deviations of asset values makes quantitative interpretation more difficult. One way to get around this is to look at the PD distribution instead (see Graph 2). As the basic Merton model uses the standard pricing model for an option with a fixed exercise date (a European option), the PD is the probability that the market value of a corporation's assets will be below the debt barrier in one year. Looking at the historical trends over the sample period, the 95th percentile, which contains the most vulnerable corporations, peaks at almost 50 per cent in early 2009. Graph 2 also illustrates the limitations of using a normal distribution to map from the D2D to the PD; only extreme events like the financial crisis are able to drive a discernible shift in the PD distribution even at the 95th percentile. Moving down the distribution, the peak PDs drop sharply: the 70th percentile peaked at around 5 per cent.
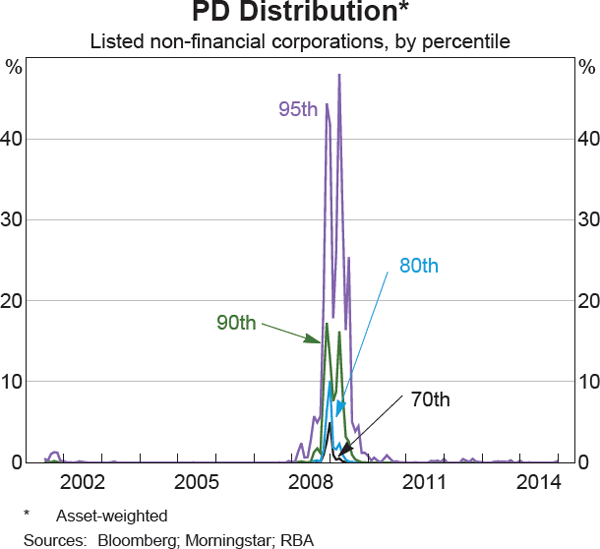
In monitoring corporate health, the Bank often analyses the information from financial statements at the broad sectoral level. This is because demand and supply shocks and business models can differ across sectors. Graph 3 shows that real estate companies have tended to be more leveraged than other companies. Higher leverage is likely to have contributed to the sharper deterioration in the median D2D for this sector during the financial crisis, although it may also have reflected the small number of real estate companies in the sample. By contrast, resource companies tend to be less leveraged. The financial health of resource companies, as measured by the D2D, has deteriorated recently, as falling commodity prices have weighed on their equity prices and made them more volatile.
Model Performance
The performance of the model in predicting corporate default can be assessed in a number of ways. At the most basic level, predicted defaults can be compared with actual defaults. Assuming that default probabilities are independent, the number of predicted defaults in a given period can be found by summing the PD of each firm. In other words, if the average PD in a period across 1,000 firms is 5 per cent, the expected number of defaults would be 50. To assess the (one-year ahead) PD, it is most appropriate to compare the aggregate PD in any month with the actual number of listed companies that default 12 months later.
However, given the simple definition of default in this model and the fact that corporate default is more likely to be a drawn-out process (for example, in practice there is the potential for outstanding debts to be restructured), a more relaxed definition of successful default prediction can be justified, with predicted defaults compared with cumulative defaults over the next 12 months. Table 1 presents the number of failures in each calendar year of the sample in absolute terms and as a proportion of the total number of non-financial corporations reporting.[5] By both number and share, failures were relatively high in the early 2000s, although they peaked around the time of the financial crisis in 2008–09. While actual failure, proxied here by entry into external administration, is an imperfect measure of default, the two are likely to be highly correlated.
A comparison of predicted and actual failures is presented in Graph 4.[6] The simplified definition of default in the model suggests caution in drawing strong conclusions from the level of predicted defaults. But the pattern of the predicted defaults series is broadly similar to that of actual failures, which is encouraging. The 2008 crisis is the dominant feature of the series, with the average level of predicted defaults a little higher in the post-crisis period than in the years prior. Given the intention is to use this tool primarily to assess aggregate or sectoral corporate health, matching the patterns of total corporate failures is more important than accurately predicting the absolute level of total failures or the failure of individual companies. Also important is the model's ability to distinguish between failing and non-failing companies.
| Year | Number of firms reporting(a) | Number failed | Per cent failed |
|---|---|---|---|
| 2001 | 1,214 | 29 | 2.4 |
| 2002 | 1,243 | 18 | 1.4 |
| 2003 | 1,345 | 28 | 2.1 |
| 2004 | 1,418 | 28 | 2.0 |
| 2005 | 1,515 | 12 | 0.8 |
| 2006 | 1,635 | 17 | 1.1 |
| 2007 | 1,748 | 19 | 1.1 |
| 2008 | 1,740 | 40 | 2.3 |
| 2009 | 1,715 | 43 | 2.5 |
| 2010 | 1,775 | 18 | 1.0 |
| 2011 | 1,787 | 23 | 1.3 |
| 2012 | 1,744 | 30 | 1.7 |
| 2013(b) | 1,727 | 1 | 0.1 |
| 2014(b) | 1,613 | 1 | 0.1 |
| Average | 1,587 | 22 | 1.4 |
|
(a) Firms reporting return on assets at the end of the calendar year Sources: Bloomberg; delisted Australia; Morningstar; RBA |
|||
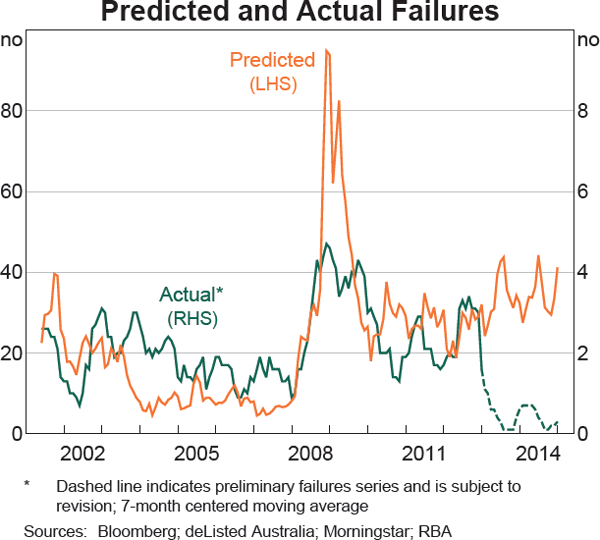
The simple comparison of predicted failures and actual failures gives a good indication of whether or not the Merton model is a useful indicator of corporate health. Another test of the usefulness of the model is whether it can adequately discriminate between corporations that are close to failure and healthier corporations. One way to do this is to compare the average PD over the 12 months leading up to failure (for the corporations that ended up failing) with the average PD for corporations that did not fail, over the same period. For this model the average PD for failing corporations is around 12 percent, while the average PD for other corporations is 1½ per cent. Statistical tests suggest that the difference between these values is significant.
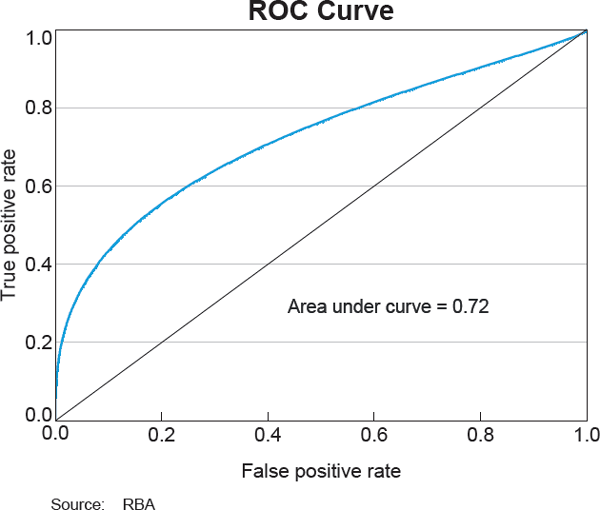
A more sophisticated way of assessing the discriminatory power of the Merton model is to use receiver operating characteristic (ROC) analysis. This approach compares the true positive rate (the number of failures that are predicted and observed, as a share of total observed failures) and the false positive rate (failures that are predicted but not observed, as a share of total observed non-failures). Observed failures are based on the data in Table 1, while predicted failures are defined by choosing a threshold and classifying all companies with reported PDs above that threshold as failed.[7] A true positive occurs when a predicted failure occurs in the 12 months prior to an observed failure. A false positive occurs when a predicted failure is not followed by an observed failure in the following year. This is an intuitive approach based on the idea that, for a given failure threshold, if two models of failure have the same number of correct failure predictions, the one that has a smaller number of incorrect predictions should be preferred.
By varying the chosen failure threshold (across the range of PD values from 0 to 1) and assessing the ratio of true positives to false positives, a ROC curve can be constructed (Graph 5). The ROC curve illustrates the trade-off between correctly identifying companies that go on to fail as ‘failing’, and incorrectly categorising companies that will survive. For low PD thresholds, the true positive and false positive rates will both be high. But as the PD threshold is increased (tightening the criteria for failure prediction) the true positive rate falls, and, if the model is informative, the false positive rate will fall faster. The area under the ROC curve (AUC) is a useful summary statistic for comparing different models. A model is considered to be an improvement over a random guess if the AUC is greater than 0.5; that is, if the ROC curve lies above a 45 degree line. The smoothed ROC curve for our baseline model, shown in Graph 5, is well above the 45 degree line and has an AUC of 0.72, which indicates that it is substantially more informative than a random guess.
Implications for Financial Stability
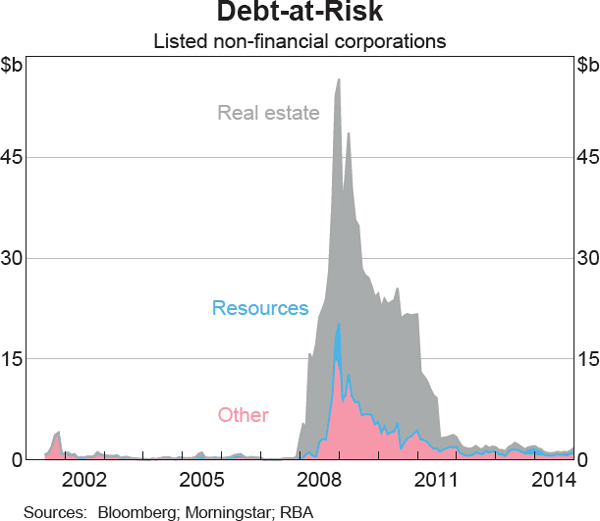
One reason that tracking the potential for corporate default is important is that it can have implications for the performance and solvency of financial institutions, which in turn can trigger episodes of systemic instability. In this context, defaults on intermediated debt are the most direct transmission channel. To assess the financial stability implications of the PDs derived from the Merton model, individual firm probabilities need to be weighted by their debt outstanding to create a measure of debt-at-risk (DAR) (Graph 6). Intermediated debt is most relevant in this case, but in the absence of reliable estimates for most corporations, total book value of debt sourced from financial statements is used.[8] The resulting series is dominated by the 2008 crisis period and its aftermath, with DAR very low in most other periods. At the sectoral level, much of the increase in the DAR reflected heavily indebted real estate companies – Centro Properties Group in particular – that were seriously affected by the crisis, although infrastructure companies (included in the ‘Other’ category) that carried a lot of debt into the crisis – such as Babcock & Brown – also contributed.[9]
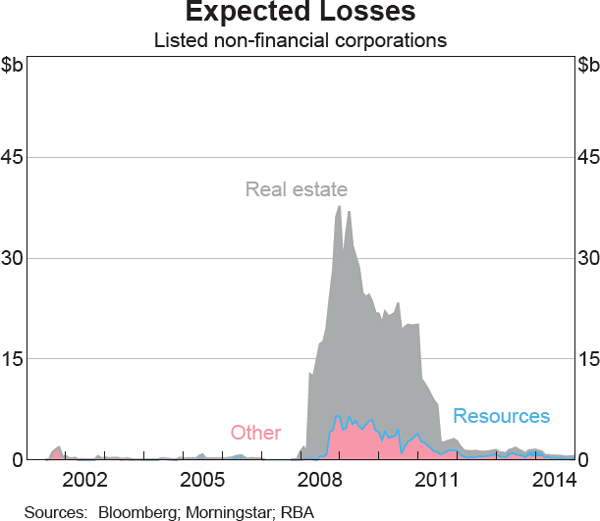
The DAR, while more relevant to financial stability than the unweighted PD, is far from a perfect measure of the impact of corporate failure. It overstates likely losses because it fails to account for potential asset recovery following failure. Another alternative – expected losses – attempts to take into account recoverable assets. The expected loss is calculated as debt-at-risk less the estimated value of assets at the 12-month horizon. The sectoral breakdown of this estimate is shown in Graph 7. It is qualitatively similar to the DAR, but it peaks at a lower level. Although they are by no means perfect analogues, and sectoral comparisons are clouded by classification issues, the broad industry trends in major banks' non-performing loans (NPLs) and specific provisions are consistent with the patterns in the industry breakdowns of DAR and expected losses. For example, loans to real estate companies accounted for a disproportionate share of the increase in banks' NPLs in the crisis period.
Conclusion
Information from financial statements is useful to analyse corporate health, but it is backward looking, available infrequently and only with a substantial lag. The systematic incorporation of more timely, forward-looking information from financial markets can enhance our ability to identify and track pockets of corporate vulnerability. The Merton model is a natural way to do this that fits comfortably within the current monitoring framework. The model's ability to identify the risks stemming from the real estate sector in 2008, and the deterioration in financial health in the resource sector more recently, indicates the value it adds as part of a suite of risk metrics.
However, the model is not without limitations. The assumption that returns are log-normally distributed is a simplification that makes the model easy to work with, but the literature suggests that stock returns are better matched by alternative, often heavy-tailed, distributions. Historical default distributions such as the one used in Moody's KMV's commercial variant of the model might improve its ability to match the observed failure series, but these data are not generally available and in any case embed an assumption that future default experience will match that seen in the past. Using such data would also come at the cost of a significantly more complex model. Another approach would be to include the distance-to-default or probability of default in a hybrid model of corporate default alongside a range of other explanatory variables from financial statements and other sources. Both approaches are currently being investigated as the Bank seeks to further enhance its ability to track corporate health.
Appendix A – The Merton model
Asset values are assumed to follow geometric Brownian-motion so that returns are log-normally distributed:
where A is the market value of assets, μ is the expected annual (risk-free) rate of return, σA is the standard deviation of asset values and τ = T−t is the horizon of interest. The probability of default is then given by:
where L is equal to the sum of total cur rent liabilities and half of non-current liabilities and Φ is the standard normal cumulative distribution function. The market value of assets and their volatility are unobservable, but the Black-Scholes option pricing model can be used in conjunction with a relationship between asset and equity volatility (which also relies on the assumption about the process characterising asset value movements) to solve for them numerically, using equity value, E, and volatility, σE, as key inputs:
where, d2 is the distance-to-default, and the probability of default is:
Expected losses in the event of default are calculated as:
this can be thought of as a put option written by the debt holders of the company for the equity holders. If the company defaults, the debt holders bear a loss equal to the difference between the liabilities outstanding and the expected value of assets. This is equivalent to paying the equity holders that amount, since under limited liability, equity holders can only lose their equity investment.
Footnotes
The author is from Financial Stability Department and acknowledges the earlier work in this area by David Rodgers. [*]
This assumption is common in constructing Merton-type models. A variation of the model based on a heavy-tailed return distribution would likely be better able to match observed equity dynamics, but this would require a more complex option pricing framework and is consequently reserved for future work. [1]
As this version of the model assumes a fixed date (European) call option equity retains value even if asset values are projected to fall below the default point within the 12-month horizon because there is a chance that future shocks will push asset values back above the default point. To the extent that some debts actually fall due beyond the 12-month horizon, the same issue might explain the higher number of defaults predicted by this model than actually observed in the Australian data. [2]
As the D2D and PD are inversely related – vulnerability is associated with a low D2D and a high PD – the most vulnerable companies are found at the opposite ends of the respective distributions. Asset-weighted distributions are presented to avoid overstating the importance of fluctuations in the D2D and PD of smaller companies. [3]
Some of the recovery following the crisis is also likely to reflect the exit of weaker companies from the sample via failure. [4]
As indicated in Graph 4, the fall in the failures series in 2013 and 2014 reflects the lag between a company entering external administration (‘failing’) and recognition of this event in the data. It is likely that the series will be revised higher in coming years. [5]
In the context of the Merton model, predicted default and predicted failure are equivalent and will be used interchangeably. [6]
For example, when the PD threshold is set at 10 per cent, all of the companies with PDs above 10 per cent are assumed to have failed and those with PDs below 10 per cent are assumed to continue trading. [7]
Trade credit accounts for the bulk of the gap between total debt and total liabilities. [8]
The sharp fall in DAR in the first half of 2011 almost entirely reflects the run-off of debt by Centro Properties Group. [9]
References
Blundell-Wignall A and C Roulet (2012), ‘Business Models of Banks, Leverage and the Distance-To-Default’, OECD Journal: Financial Market Trends, 2012/2, No 103.
Crosbie P and J Bohn (2003), ‘Modelling Default Risk’, Moody's KMV Company.
Danmarks Nationalbank (2009), Financial Stability, 1st Half 2009.
Gizycki M and B Goldsworthy (1999), ‘Australian Banking Risk: The stock market's assessment and the relationship between capital and asset volatility’, RBA Research Discussion Paper No 1999-09.
Hillegeist SA, EK Keating, DP Cram and KG Lundstedt (2004), ‘Assessing the Probability of Bankruptcy’, Review of Accounting Studies, 9(1), pp5–34.
IMF (International Monetary Fund) (2009), ‘How Vulnerable Are Non-financial Firms?’, World Economic Outlook: Crisis and Recovery, World Economic and Financial Surveys, IMF, Washington DC, pp 20–22.
Merton R (1974), ‘On the Pricing of Corporate Debt: The risk structure of interest rates’, The Journal of Finance, Vol (2), pp 449–470.
Rodgers D (2015), ‘Credit Losses at Australian Banks: 1980–2013’, RBA Research Discussion Paper 2015-06.
Saldias M (2012), ‘Systemic Risk Analysis Using Forward-Looking Distance-To-Default Series’, Federal Reserve Bank of Cleveland Working Paper, No 10–05.
Tudela M and G Young (2003), ‘A Merton-Model Approach to Assessing Default Risk in UK Public Companies’, Bank of England Working Paper, No 194.