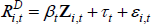RDP 2018-05: Do Interest Rates Affect Business Investment? Evidence from Australian Company-level Data Appendix C: Multiple Imputation Model
April 2018
- Download the Paper 1,258KB
As noted above, to use MI we need to specify a model for imputation. We model interest rates as:
where Zi,t is a vector of variables taken from the company's balance sheet that may be related to its riskiness, demand for credit, and interest rates more generally. These variables include: assets; the return on assets; the debt-to-assets ratio; the liquidity ratio (the ratio of cash to current liabilities); years since listing (in levels and squared terms); Tobin's average q; D2D. It also includes a number of indicators that take on the value one if: the company's D2D was in the bottom quartile; the company made a loss in the year; the company had negative equity; the company delisted within the next two years; the company was small (assets below the median); or if the company was of medium size (assets between the median and the 75th percentile). The coefficients on the variables in Zi,t are allowed to vary over time.[28]
A common approach is to use the output from the linear regression plus some random noise as the imputed values. The method is parametric, as the errors are assumed to be normally distributed when the noise is added. Instead, we use a method called predictive mean matching (PMM), first suggested in Little (1988). This is a semi-parametric approach that tends to be more robust than the fully parametric approach if the imputation model is misspecified (e.g. Schenker and Taylor 1996). Given the relationship between interest rates and the variables in Zi,t is likely to be highly nonlinear, we prefer this more robust approach.[29]
PMM uses a parametric linear regression, followed by a non-parametric nearest-neighbour regression. More formally, PMM involves six steps:
-
The imputation model is estimated using the complete data, yielding coefficients
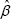 .
.
-
Coefficients β* are drawn from the posterior distribution of
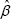 (assuming the errors are normally distributed).
(assuming the errors are normally distributed).
-
Values are imputed for the missing observations
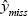 using β*.
using β*.
-
Values are imputed for the complete observation
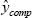 using β*.
using β*.
-
For each
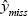 , we identify the k closest completed observations based on their imputed values
, we identify the k closest completed observations based on their imputed values 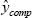 .
.
- We randomly choose one of these k completed observations, and use its true observed value ycomp as the actual imputed value ymiss.
The collection of ycomp and ymss can then be used to estimate the relationship of interest.
The choice of k represents a trade-off between efficiency and bias (similar to the choice of bandwidth in a kernel regression). Choosing k to be too low can lead to a loss of efficiency, as the imputed value for each observation can vary wildly between iterations. Choosing k to be too high could induce bias into the estimation, particularly if the observations are sparse. We set k = 3, which is relatively common in the literature. The results appear to be reasonably robust to the choice of k. We run the imputation and estimation 100 times. This is higher than the minimum number of iterations recommended in papers such as Bodner (2008).