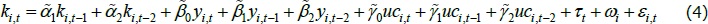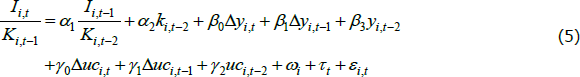RDP 2018-05: Do Interest Rates Affect Business Investment? Evidence from Australian Company-level Data 3. Reduced-form Model
April 2018
- Download the Paper 1,258KB
3.1 Model Specification
Our reduced-form model specification is very similar to that in La Cava (2005). The model can be derived from a firm optimisation problem with a constant elasticity of substitution production function and adjustment costs (Bond and Van Reenen 2007). In the absence of adjustment costs, the company chooses an optimal level of real capital (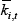 ) as a function of real sales (yi,t) and the real user cost of capital (uci,t), all measured in logs:
) as a function of real sales (yi,t) and the real user cost of capital (uci,t), all measured in logs:
where ai,t is an intercept that accounts for productivity shocks and σ is the elasticity of substitution between labour and capital. The user cost reflects the cost of investment, while the level of sales captures the company's investment ‘fundamentals’ (Gilchrist and Zakrajšek 2007).
Due to adjustment costs, the company's actual capital stock (ki,t) may diverge from the optimal capital stock. As such, there will be a long-run optimal level towards which the capital stock should adjust, as well as short-run dynamics (associated with the past values of capital, sales and the cost of capital). To account for this, Equation (3) can be nested in a general dynamic model which includes lags of independent and dependent variables:[12]
where ωi is a company fixed effect and τt is a year fixed effect. The company fixed effect captures time-invariant company-specific factors, such as their average productivity or business model. The time fixed effects capture aggregate influences, such as the business cycle, aggregate uncertainty and economy-wide changes in the relative price of capital goods.
This model can be re-parameterised as an error correction model (ECM), which allows for easy identification of the long- and short-run dynamics:
where 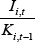 is the net investment rate, which is approximately the log change in the capital stock.
is the net investment rate, which is approximately the log change in the capital stock.
We are mainly interested in the coefficients on the cost of capital terms (i.e. γ0, γ1 and γ2). If these coefficients are estimated to be negative, it suggests that a lower cost of capital is associated with higher investment. Moreover, if γ2 is significant, and the speed of adjustment coefficient α2 is significantly negative, it suggests that there is a long-run inverse relationship between the cost of capital and the level of capital.
Fixed-effects estimation of Equation (5) is inconsistent due to the inclusion of a lagged dependent variable (which is correlated with the error term). As such, we estimate the model using the Arellano-Bond dynamic panel generalised method of moments (GMM) estimator (Arellano and Bond 1991).
For estimation, the model specification is adjusted slightly. First, the user cost of capital is replaced with either the cost of debt or the cost of finance.[13] The user cost of capital is a broader measure than the cost of debt or finance. It not only includes the cost of finance, but also includes a component to account for the tax treatment of revenue and depreciation, and a component to capture the relative price of capital goods. We focus on the cost of debt and finance as we want to specifically examine their relationship with investment, abstracting from these other factors.[14]
The second departure is that one of our investment measures is a gross measure, whereas the relationship in Equation (5) is derived for a net measure (change in the capital stock). While this should not introduce any estimation issues, the model is no longer an ECM as gross investment is not the change in the capital stock. Therefore, while we continue to use the same framework for ease of exposition, our focus is on the short-run relationship when using gross investment.
3.2 Results
3.2.1 Cost of debt
Table 1 contains the estimated coefficients using the cost of debt.
| Net investment | Gross investment | |
|---|---|---|
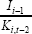 |
−0.52*** (0.14) |
−0.23** (0.10) |
| ki,t−2 | −0.63** (0.31) |
0.05 (0.14) |
| Cost of debt | ||
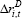 |
−0.47*** (0.14) |
−0.24** (0.12) |
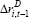 |
−0.63** (0.26) |
−0.31 (0.20) |
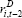 |
−0.92** (0.43) |
−0.30 (0.33) |
| Sales | ||
| Δyi,t | 0.15*** (0.05) |
0.16*** (0.06) |
| Δyi,t−1 | −0.01 (0.09) |
−0.12 (0.07) |
| yi,t−2 | −0.15 (0.17) |
−0.18 (0.15) |
| Observations | 259 | 264 |
|
Notes: *, **, *** indicate significance at the 10, 5 and 1 per cent levels, respectively; standard errors are reported in parentheses and are robust to autocorrelation and heteroskedasticity; estimated using Arellano-Bond dynamic panel GMM estimator |
||
For net investment, a decrease in the cost of debt leads to higher investment in the short run and to a higher level of capital in the long run. This is shown by the coefficients on the interest rate terms. Both of these relationships are statistically significant.[15] To get a sense of the dynamics and the economic significance, Figure 7 shows the effect of a permanent 1 per cent decrease in the cost of debt on the rate of investment (confidence intervals are constructed using bootstrapping).[16] The lower cost of debt increases the investment rate by around ½ percentage point within two years, before its effect dissipates. Accordingly, the capital stock rises by around 1½ per cent. This implies that the elasticity of the capital stock with respect to the cost of debt is 1½. This is broadly consistent with estimates of the elasticity of the capital stock with respect to the user cost of capital for Australia (La Cava 2005), and for other small open economies such as Canada (Schaller 2006). Considering gross investment, there is again evidence consistent with a lower cost of debt being associated with higher investment. Overall, the results indicate that borrowing rates have a direct effect on the investment of indebted companies.[17]
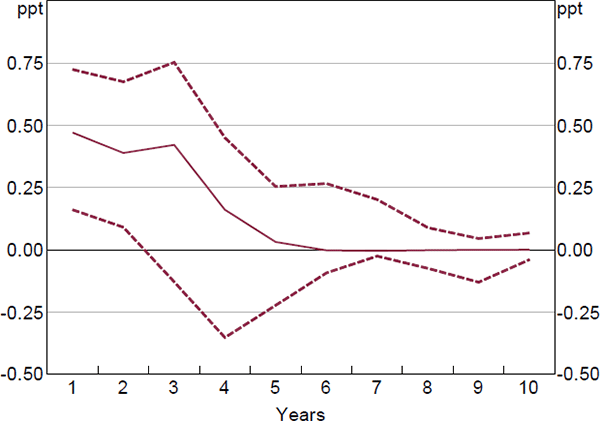
Notes: Model using net investment and the cost of debt; dashed lines are bootstrapped 90 per cent confidence intervals
As a robustness test, we also estimated the model treating sales and interest rates as predetermined variables, rather than as strictly exogenous variables. This involves using a reduced set of instruments for the GMM estimation. The results (not shown) are reasonably similar, and continue to show a negative relationship between investment and interest rates. We also found no evidence of serial correlation in the errors at an order above one in the main model, suggesting that the instruments are valid.[18]
Importantly, our results do not necessarily indicate why there is a link between interest rates and investment. For this, we would need to isolate a plausibly exogenous source of variation in interest rates, which is inherently difficult. But we can rule out some explanations. For example, the relationship does not appear to be due to monetary policy, at least not directly, as we control for aggregate business cycle variables through time fixed effects. And it does not appear to be due to company risk, as the results are nearly identical if we control for indicators such as D2D. Moreover, it does not appear to reflect the fact that sales are a backward-looking measure of demand, whereas interest rates and investment might be affected by the outlook for future sales, as the relationship still holds when we estimate a model including a forward-looking measure of demand: Tobin's q (see Appendix B).
Instead, we hypothesise that the inverse relationship between interest rates and investment is due to credit supply effects. A relaxation of lending standards leads to lower interest rate spreads (for a given company profile), which encourages more investment.[19] The relationship could also reflect differential timing in the repricing of debt, with some companies having to refinance during periods of high rates, such as the financial crisis, and others not. Those that do not have to refinance will face lower rates and so may invest more, all else equal. In many senses, this is quite similar to an idiosyncratic credit supply shock.
Consistent with La Cava (2005), the estimated coefficient on the lag of investment is negative and significant, indicating negative autocorrelation. So periods of high investment tend to be followed by periods of lower investment. This is at odds with models that incorporate convex adjustment costs in order to smooth investment over time (for a discussion, see Bond and Van Reenen (2007)); it is more consistent with companies investing in bursts, potentially due to the lumpy nature of larger projects (e.g. a new factory).
3.2.2 Cost of finance
Table 2 contains the estimated coefficients using the cost of finance. There is no evidence of a significant negative relationship between the cost of finance and investment using either gross or net investment, for either the sectoral or company-specific measures of the cost of equity.
The leading explanation for finding a significant negative relationship between investment and the cost of debt, but not the cost of finance, is that the cost of equity is poorly measured. This is not entirely surprising given that the cost of equity is unobserved and hard to measure. Companies have noted this as part of the RBA's business liaison programme (Lane and Rosewall 2015).[20]
An alternative explanation is the sample. When we switch from the cost of debt to the cost of finance the sample expands, as it now includes companies that have no debt (and as such have no borrowing rate data). If companies with no debt are less responsive to changes in the marginal costs of debt and finance – for example, because they are credit constrained – this could help to explain why the coefficients are no longer statistically significant. It would also suggest that our earlier findings for the cost of debt are subject to sample selection bias, and are only representative for the sub-sample of companies with debt.
| Company-specific | Sectoral | ||||
|---|---|---|---|---|---|
| Net investment | Gross investment | Net investment | Gross investment | ||
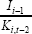 |
−0.22 (0.16) |
−0.74*** (0.08) |
0.11 (0.14) |
−0.66*** (0.14) |
|
| ki,t−2 | −0.25 (0.33) |
−0.49*** (0.15) |
0.31 (0.52) |
−0.62*** (0.27) |
|
| Cost of finance | |||||
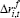 |
0.15 (0.10) |
0.01 (0.10) |
0.18 (0.32) |
0.03 (0.10) |
|
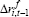 |
0.26 (0.28) |
0.23 (0.17) |
1.04 (0.94) |
0.41*** (0.14) |
|
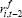 |
−0.32 (0.50) |
0.64*** (0.24) |
0.91 (1.39) |
0.77*** (0.26) |
|
| Sales | |||||
| Δyi,t | 0.13* (0.08) |
0.16*** (0.07) |
0.15** (0.07) |
0.12*** (0.03) |
|
| Δyi,t−1 | −0.02 (0.12) |
0.22*** (0.09) |
−0.61 (0.43) |
−0.01 (0.10) |
|
| yi,t−2 | −0.21 (0.20) |
0.55*** (0.18) |
−0.80* (0.48) |
0.20 (0.22) |
|
| Observations | 320 | 330 | 343 | 352 | |
|
Notes: *, **, *** indicate significance at the 10, 5 and 1 per cent levels, respectively; standard errors are reported in parentheses and are robust to autocorrelation and heteroskedasticity; estimated using Arellano-Bond dynamic panel GMM estimator |
|||||
One simple way to test whether the result is due to sampling is to estimate the cost of finance models over a reduced sample that only includes companies with debt. If the coefficients are different to those obtained by estimating the model over the full sample, it would suggest that companies with debt have a different elasticity of investment with respect to the cost of finance, and therefore potentially a different elasticity with respect to the cost of debt.
Estimating the model over the sub-sample of companies with debt leads to quite similar coefficients on the cost of finance (not shown). This suggests that our results for the cost of debt are not materially affected by any sample selection biases. We examine this further below.
Footnotes
The choice to include two lags is somewhat arbitrary. However, given the data are annual and the sample is relatively short, using longer lag specifications will likely lead to less precise estimates. [12]
We take the rate payable at the end of the financial year to be the marginal rate the company faces over the next year. For example, if a company's average interest rate payable on debt as at 30 June 2005 is 5 per cent, we take 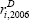 to be 5 per cent.
[13]
to be 5 per cent.
[13]
The relationship in Equation (5) is for the cost of capital, but excluding components such as the relative price of capital goods should not introduce any particular biases. Such components are generally measured at an aggregate or sectoral level and are additively separable when the user cost of capital is defined in logs. As such, they should be relatively well captured by the company and time fixed effects. Even if they are not well captured, their exclusion should not pose major problems as there is unlikely to be much correlation between these aggregated measures and the company-specific measures of the cost of finance. Moreover, leaving these components out of the long-run relationship should not lead to any estimation issues, even if the variables are non-stationary. In a time-series regression, if the variables were non-stationary we would need to have a properly specified cointegrating relationship to ensure that the errors are stationary, or else inference would be invalid. However, this is less of a concern in a panel regression, particularly if the panel is made up of a short time series and large cross-section, as is the case here (e.g. Hsiao 2003). Still, it does suggest some caution in interpreting any long-run relationships. [14]
We considered examining whether the elasticities differed for companies of different sizes or risk profiles, but the sample was too small. [15]
Instead of sampling individual company-year observations with replacement, we sample companies. This maintains the dependence structure within the data. We bootstrap 1,000 times. [16]
The results are robust to including cash flow (as measured by the ratio of earnings before interest, tax, depreciation and amortisation to total assets) in the model. [17]
An alternative test is the Sargan test of over-identifying restrictions, but this tends to perform relatively poorly in the presence of heteroskedasticity (Arellano and Bond 1991). [18]
The relationship may also reflect variation in the mix of debt instruments held by companies. The companies facing higher interest rates could be relying on more expensive forms of borrowing, such as credit cards or overdrafts, rather than bank loans or corporate bonds. Our estimates combine these debt instruments. It may be that companies shift towards cheaper borrowing instruments when they invest. Though, as we use interest rates as at the beginning of the year, it is unlikely that such behaviour is materially affecting our results. [19]
We experimented with using one noisy measure of the cost of finance as an instrument for the other in the vein of Ashenfelter and Krueger (1994). While there is slightly more evidence of a negative relationship between the cost of finance and investment the results were still not significant. Moreover, the cost of finance measures appear to be relatively weak instruments for each other. [20]