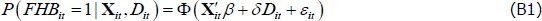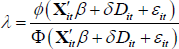RDP 2017-05: The Property Ladder after the Financial Crisis: The First Step is a Stretch but Those Who Make It Are Doing OK Appendix B: Heckman Selection Model
September 2017
In estimating the determinants of FHB indebtedness we are faced with the problem that we only observe debt for households who have chosen to become FHBs and taken on a mortgage. Since households become indebted FHBs in a non-random way, based on characteristics such as marriage, education and employment status, we need to account for the potential bias in our estimates induced by this non-random selection.
To address this issue, we adopt the standard approach of a sample selection correction model or Heckit method which was first proposed by Heckman (1976, 1979). A summary of this two-stage procedure is provided below.
B.1 Stage One: Selection Equation
We use a probit model for the ‘selection’ equation to estimate the probability of transitioning from being a renter to an FHB (using a sample of both renters and FHBs). We then compute an inverse Mills ratio for each observation.
The selection equation used is identical to Equation (1) and takes the form:
where the dependent variable FHBit is binary and equal to one if household i took out a mortgage to purchase their first home between survey years t − 1 and t. The term Dit is a post-2007 dummy equal to one if the year household i became an FHB is greater than 2007 and Xit is a vector of household and aggregate-level controls. ϕ is the standard normal probability density function and Φ is the standard normal cumulative distribution function. The vector of controls used is identical to Model 3 in Table 2. Following Greene (2003), the inverse Mills ratio, λ, is calculated as:
B.2 Stage Two: Linear Regression Model
For the second-stage regression, we run a linear regression on a sample of FHBs only. We include all of the variables used in the selection equation above, except for age and age squared, and also the inverse Mills ratio from the first-stage regression as an additional variable.
A common assumption when using the Heckit method is that the vector of controls in the selection model contains all of the variables that are included in the second-stage regression. However, while the model is technically identified in this case, it is usually desirable to exclude at least one variable in the selection model from the second stage or the second-stage regression is likely to suffer from collinearity problems.
In this case, the criteria for a variable being excluded is that it is correlated with the decision to become an FHB but has no direct effect on the level of debt an FHB takes on. We select the variable age (and age squared) as the exclusion restriction here, as the age of the household reference person is likely to have a direct bearing on when the household decides to purchase their first home, but unlikely to have a bearing on the level of debt they decide to take on. If our sample included all households taking on new mortgage debt, age would likely influence the amount of debt households are willing to take on. However, given the narrower age range of FHBs, age is less likely to play a role (i.e. a 25-year old FHB household is likely to face a similar decision of how much debt to acquire as a 35-year old FHB household, all else equal). In addition to this argument, we find that when age and age squared are included in the second-stage regression they are insignificant – although their inclusion affects the other coefficient estimates and their significance, likely reflecting collinearity problems.
This standard Heckman selection method is used for the mean regression model. For the median regression model shown in Table C3, we follow a similar approach to Buchinsky and Hahn (1998) and Atalay et al (2015) and include the inverse Mills ratio and its squared value.