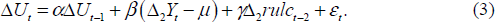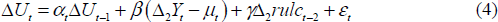RDP 2015-14: Okun's Law and Potential Output 3. Models

We present two models of Okun's law in changes.

3.1 Constant Coefficients Model

A simple benchmark with constant coefficients is estimated by OLS.

ΔU is the one-quarter change in the unemployment rate, Δ₂Y is two-quarter annualised growth in log GDP and μ is the annualised growth rate of potential GDP. So Δ₂Y − μ is the annualised two-quarter change in the output gap. Δ₂rulc is the annualised two-quarter change in log real unit labour costs.

A few features of our specification are not conventional. Our lag structure is chosen so as to help explain the data. We do not include the change in the NAIRU, or the levels of either the NAIRU or potential output, for reasons we explain in Section 6. And perhaps most unusual is our inclusion of real unit labour costs. We interpret this term as reflecting factor substitution. When the relative cost of labour increases, firms seek to increase labour productivity and lower their demand for labour for a given level of output, raising unemployment. This effect is frequently mentioned in discussions of the determinants of Australian unemployment, and we are somewhat surprised that it does not seem to have been included in Okun's law specifications before. This is particularly so as the econometric evidence of its importance is strong, with a t-statistic of 4 in our preferred model. In principle, increases in real unit labour costs boost labour productivity and hence could increase the level of potential output. However, this interaction is small (especially if a reduction in capital productivity is assumed) and we ignore it below.

3.2 Time-varying Coefficients Model

Our preferred model allows potential GDP growth μ, and the coefficient on the lagged dependent variable α, to vary over time (hence we write them with a subscript t). We assume both of these parameters follow random walks, and we estimate them with the Kalman filter.

We specify a measurement equation:

and state equations

To initialise the Kalman filter, we assume potential GDP growth in 1960:Q2 was 4 per cent, with a variance of 5 percentage points, equal to the average rate and variance of annual GDP growth in the 1950s. We assume a zero starting value for the coefficient on our lagged dependent variable, with a variance of 1. Other priors produce different results in the first few years of estimation but converge by the late 1960s.