RDP 2015-14: Okun's Law and Potential Output 4. Estimation
December 2015 – ISSN 1448-5109 (Online)
- Download the Paper 987KB
We estimate both models over the period 1960:Q3 to 2015:Q1 using EViews default settings, except where noted.
4.1 Data
We use three series for estimation: real GDP, the unemployment rate and real unit labour costs, each of which is quarterly and seasonally adjusted. These data and estimation code are publicly available at <http://www.rba.gov.au/publications/rdp/2015/2015-14-data.html>. GDP data are sourced from the national accounts. Unemployment rate estimates are from the ABS Labour Force Survey, back to 1966:Q3. For earlier data, we use estimates for unemployment (number of persons) and the labour force from the ABS ‘Modellers’ Database, Jun Qtr 2014' (ABS Cat No 1364.0.15.003).
Real unit labour costs are obtained from internal RBA databases. They are defined as the sum of compensation of employees (COE) and payroll taxes paid, less government employment subsidies received, divided by the product of real non-farm GDP and the implicit price deflator for gross national expenditure. The ratios of employment subsidies and payroll taxes to COE are assumed not to change until 1978:Q3 and 1972:Q3 respectively, when quarterly estimates begin.
4.2 Results
Table 1 presents estimated coefficients. We also report the long-run response of unemployment to changes in output, known as ‘Okun's coefficient’, which equals:[4]
| Parameter | Description | Constant coefficients | Time-varying coefficients |
|---|---|---|---|
| α, α2015:Q1 | Lagged dependent variable |
0.310 (0.064) |
0.443(a) (0.251) |
| β | Change in output gap |
−0.047 (0.008) |
−0.049 (0.006) |
| μ, μ2015:Q1 | Potential output growth |
3.69 (0.343) |
2.94(a) (0.781) |
| γ | Change in real unit labour costs | 0.016 (0.005) |
0.019 (0.004) |
| σε | Standard deviation of measurement equation error | 0.233 | |
| σν | Standard deviation of potential output equation error | 0.124 | |
| σw | Standard deviation of inertia equation error | 0.044 | |
| (4 *β)/(1 − α) | Long-run effect of output on unemployment (‘Okun's coefficient’) |
−0.27 | −0.35(a) |
| Equation standard error | 0.246 | ||
| Adjusted R2 | 0.43 | ||
| Estimation method | OLS, with White (1980) standard errors | Kalman filter |
|
|
Notes: Standard errors reported in parentheses (a) Time-varying parameter as at 2015:Q1 |
|||
Multiplication is by 4 because changes in output are annualised. Apart from the time-varying coefficients, the estimates for the two models are very similar. In particular, they have essentially the same coefficients on the change in the output gap and the change in real unit labour costs. As can be seen by comparing the standard error of the OLS equation (0.246) with its Kalman filter analogue, the standard deviation of measurement equation prediction errors (0.233), the model with time-varying coefficients fits the data somewhat better.
The upper panel of Figure 1 compares fitted values from the Kalman filter (on an annual change basis, to reduce clutter) with actual changes in the unemployment rate. The model seems to explain most of the variation in the data. Fitted values from the constant coefficients model are not shown but look very similar.
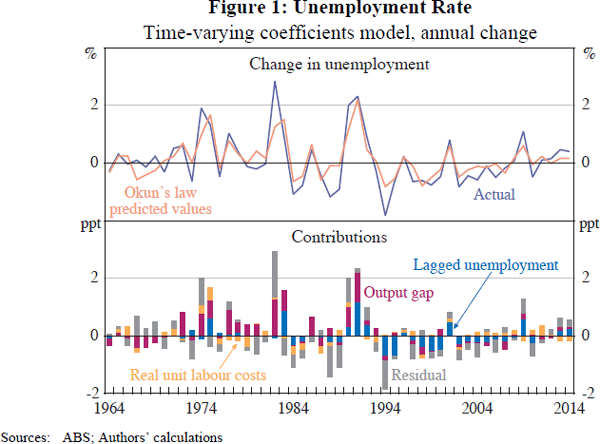
The lower panel of Figure 1 shows estimated contributions to changes in the unemployment rate. Most of the model's explanatory power comes from changes in the output gap. We discuss this effect, and its stability over time, in more detail in Section 4.3.
Real unit labour costs have had a clear and important influence on the Australian unemployment rate, with a coefficient that is highly statistically significant in both models. Long-run effects change over time due to interaction with the coefficient on the lagged dependent variable. As a guide, the largest response followed the 12 per cent (0.112 log points) increase in real unit labour costs over the five quarters to 1975:Q1. We estimate that this increase, if sustained, would have raised the unemployment rate by 1.1 percentage points in addition to its effects on the output gap. Since the late 1980s, real unit labour costs have been more stable and hence less important for explaining changes in unemployment.
Inclusion of real unit labour costs does not greatly affect other results. Without it, our residuals would be even more skewed – because some of the largest increases in unemployment, in 1975 and 1982, are partly explained by large increases in real unit labour costs. We discuss skewness in Section 6.1. Our estimate of the variance of changes in potential output growth would be slightly smaller, giving rise to a slightly flatter decline in potential over the past two decades, with a final (2015:Q1) estimate of 3.1 per cent. And, as mentioned in Section 5, recent forecasts would be slightly more accurate.
4.3 Time-varying Parameters
OLS estimates of Okun's law are unstable over time. This can be seen, for example, in Quandt-Andrews tests of parameter instability at unknown breakpoints, where the hypothesis of constant parameters is rejected with a p-value of 2 per cent.[5] Tests of stability for individual coefficients, and rolling regressions, indicate that this instability is attributable to the intercept and to the coefficient on the lagged dependent variable. Accordingly, we model these as time-varying parameters.
As shown in Figure 2, we estimate that potential GDP growth fell from around 5 per cent in the 1970s to 2.9 per cent at 2015:Q1.[6] Here, and henceforth in the text, we translate our regression estimates into approximate annualised percentage changes by multiplying coefficients on quarterly log differences by 400. Figure 2 also shows a one standard deviation range about the point estimates. Assuming normality, a 68 per cent confidence interval for the 2015:Q1 estimate spans 2.2 to 3.7 per cent.
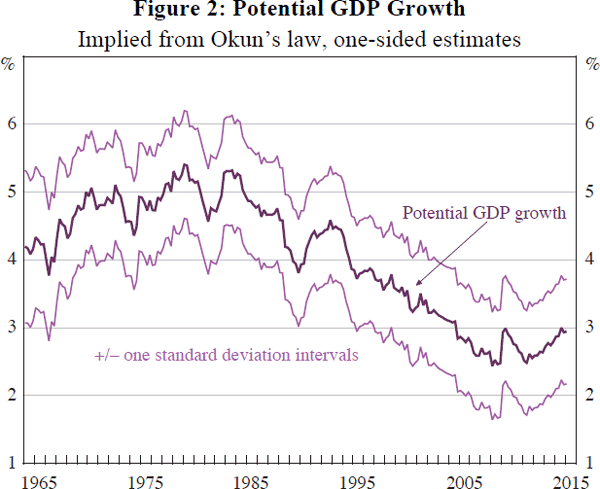
Recent estimates of potential GDP growth have increased over recent years. This reflects an upward drift in the unemployment rate, averaging one quarter of a percentage point a year since 2011. Given that GDP growth was averaging about 2½ per cent a year, near its estimated potential rate, this surprised our model. The Kalman filter takes these surprises as a signal that its estimate of the output growth required to stabilise unemployment was too low, and revises it higher.
The sharpest changes in potential output growth tend to occur when unemployment rises suddenly, as in 1991 and 2009. This reflects the skewness of changes in unemployment. As we discuss in Section 6.1, our model is able to account for much, though not all, of this skewness.
An interesting feature of our estimates is that revisions to potential are positively correlated with surprises to unemployment, given output. These surprises usually involve increases in the growth rates of labour force participation or productivity, some of which the model estimates to be permanent. This countercyclical behaviour of potential is offset by procyclical revisions to potential when output is surprisingly strong, given unemployment. When GDP and unemployment move predictably together over the cycle, as will be true on average, potential will be unrevised.
Our estimate of potential output growth in the 1970s of around 5 per cent is relatively high. In contrast, the ‘production function’ approach of the IMF and OECD tends to produce estimates for this period that are quite low. This largely reflects a conceptual difference. Our measure refers to expected (or ex ante) growth rates, the measure that is relevant for forecasting, whereas production function estimates refer to realised (or ex post) changes. The latter will include shifts in the level of potential output. An estimated increase in the NAIRU lowered ex post growth rates in the 1970s. But level shifts that are not expected to continue do not affect expected growth rates.
An advantage of production function approaches is that they can decompose changes in potential output growth – an issue on which our model is silent. Unfortunately, we are not aware of a recently published decomposition. However, our understanding of this approach is that it would also point to a substantial slowdown in potential output growth several decades ago, attributable to roughly similar reductions in the contributions from labour, capital and productivity.
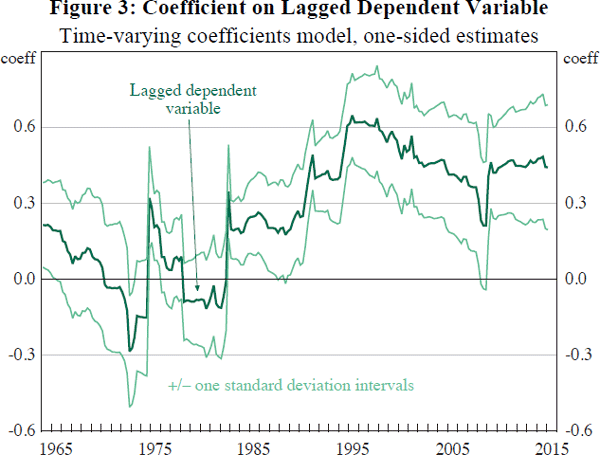
Our other time-varying parameter αt, shown in Figure 3, rarely attracts attention outside the world of unemployment forecasters. It captures the increasing persistence of movements in the unemployment rate. In the early part of our sample, movements in the unemployment rate were often transitory, but in recent decades they appear to have become quite persistent. We suspect that a large part of this change reflects measurement improvements. Advances in technique and sample size considerably reduce the noise evident in the early part of the sample. In particular, the introduction of rotation sampling in 1978 imposed a moving average term on the level of the unemployment rate.[7]
In contrast, the short-run response of changes in unemployment to changes in output has been surprisingly stable over time. To illustrate, the solid lines in Figure 4 show least squares estimates from three separate sub-samples of similar length. A percentage point decrease in the output gap is estimated to raise the unemployment rate within two quarters by about a quarter of a percentage point in each sub-sample.
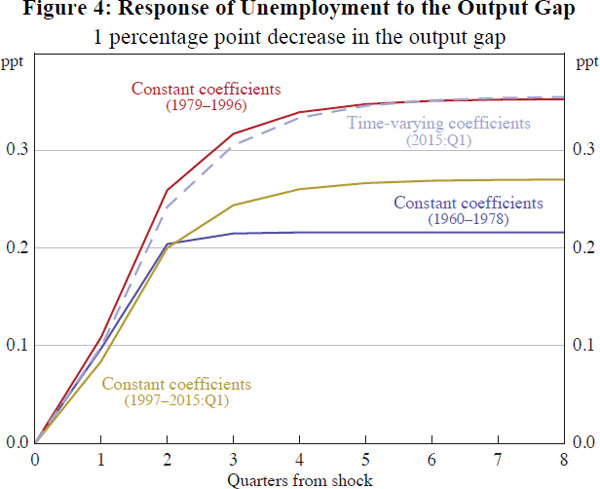
This stability has implications for views on structural change in the labour market. It is common to hear speculation that behaviour has changed over time: for example, because labour hoarding is more or less common or because workers transition between categories differently. The essentially unchanged short-run response of unemployment to GDP over several generations does not refute these hypotheses, but it does invite scepticism about their broader macroeconomic importance.
There is more variation in the longer-run effects, reflecting changes in estimates of persistence. For comparison, the dashed line in Figure 4 shows estimated responses from our time-varying coefficients model using parameter values at the end of our estimation sample. This model estimates a similar initial impact to the three least squares estimates. Reflecting the high level of persistence at the end of the sample, the long-run effect (the ‘Okun coefficient’) is relatively large, at −0.36 percentage points.
The stability of the coefficient on real unit labour costs is difficult to assess. Most of the variation in this variable occurred in the 1970s and 1980s, with more recent data being uninformative.
Footnotes
Our estimate holds real unit labour costs constant whereas other researchers often allow other variables to change. In practice, this difference is unimportant. [4]
Based on Exp-F tests with a 15 per cent trim and Newey-West covariance matrix; other tests give essentially the same result. [5]
We estimate potential GDP growth was close to 5 per cent in the 1960s also. However, this reflects a significant weight on the initial prior value required for Kalman filter estimation, so we do not emphasise this as a finding. [6]
Most of the increase in this coefficient occurred in the 1980s and pre-dates a substantial trend decline in the unemployment rate. Hence asymmetry in unemployment rate movements, discussed in the following section, is unlikely to be an explanation. [7]
