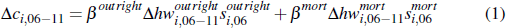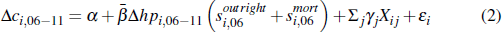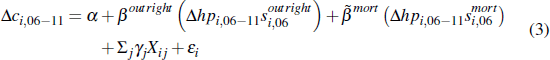RDP 2015-08: Housing Wealth Effects: Cross-sectional Evidence from New Vehicle Registrations 4. Regression Analysis

Having seen graphical evidence of a relationship between house prices and new vehicle registrations in Figure 3, we now move to a regression framework. This allows us to estimate the relationship between house prices and new vehicle registrations controlling for determinants of consumption growth other than housing wealth.

We begin by noting that, for postcode i, the relationship between a change in housing wealth and consumption is given by the following expression:

where Δc_i,06–11 is the log change in consumption in postcode i between 2006 and 2011, β^outright is the propensity of those owning their home outright to consume out of a change in housing wealth, 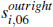is the share of outright home owners in postcode i in 2006, 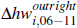is the log change in housing wealth for outright home owners in postcode i between 2006 and 2011, and analogously for mortgagors.

For outright home owners, the change in housing wealth varies one-for-one with the change in house prices. But for households with a mortgage, home equity wealth varies more than one-for-one with house prices. For example, for a household with an initial 80 per cent loan-to-valuation ratio, a 10 per cent increase in the price of their house raises home equity wealth by 50 per cent.

Unfortunately, we do not have data on average leverage of mortgagors by postcode.^[8] We take two approaches to deal with this data limitation. Under the first approach, we group outright owners and mortgagors together, implicitly ignoring mortgage debt and considering the effect of gross housing wealth on consumption. In this case, we estimate the regression:

where Δc_i,06–11 is the log change in new passenger vehicle registrations in postcode i between 2006 and 2011, Δhp_i,06–11 is the log change in house prices over the same period, 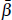is the relationship between gross housing wealth and new vehicle registrations, α is a constant term, and X_ij is control variable j for postcode i.

Under the second approach, we attempt to identify the reduced-form effect of a change in house prices on new vehicle registrations for mortgagors using variation in housing-tenure type across postcodes. This approach implies the following regression specification:

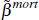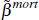where is the reduced form relationship between house prices and new vehicle registrations for mortgagors. If the collateral constraint channel is significant, then should be larger than β^outright, because it comprises the consumption response via both a standard wealth effects channel and a collateral constraints channel.

The vector of controls includes all relevant census variables in 2006 levels, and in differenced form for the period 2006 to 2011. The vector of controls also includes each postcode's distance to the CBD, and a dummy variable for waterfront postcodes. These geographic variables absorb any predictable variation in relative house price growth that is correlated with proximity to the CBD.^[9] They also control for the possibility that households living in postcodes at greater distances from the CBD may have a higher propensity to spend an additional dollar of wealth on new passenger vehicles than households in inner-city postcodes.^[10]

We express passenger vehicle registrations in per capita terms to control for differences in population growth across postcodes. We use weighted least squares to estimate each regression, with the 2006 population for each postcode as weights. This makes postcodes with a large population relatively more influential in estimating the regression parameters, which is appropriate because each postcode-level observation represents an average over a relatively large number of households.

To reduce the influence of extreme observations we exclude a small number of postcodes from our analysis: we exclude postcodes experiencing a change in per capita new vehicle registrations greater than 75 per cent in magnitude between 2006 and 2011, or more than a 0.025 magnitude change in per capita new passenger vehicle registrations when analysing changes in the number of vehicles purchased. Extreme observations have a negligible effect on the elasticity or average MPC estimates, but do affect our ability to detect heterogeneity in MPCs across postcodes.

Footnotes

The Census reports data on the level of monthly mortgage payments, but we do not know loan balance. The HILDA Survey contains more detailed information on households with a mortgage, but the sample size of the survey is too small to make reliable inference about differences in loan-to-valuation ratios across postcodes. Unfortunately, the loan-level data used by Read, Stewart and La Cava (2014) is unsuited to estimating average loan-to-valuation ratios by postcode. [8]

See see Kulish, Richards and Gillitzer (2012) for evidence on the relationship between distance from the CBD and waterfront proximity with the level and growth rate of house prices. [9]

Thanks to Anthony Richards for providing the data on waterfront postcodes. [10]