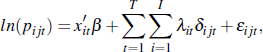RDP 2015-08: Housing Wealth Effects: Cross-sectional Evidence from New Vehicle Registrations 2. Data
August 2015 – ISSN 1448-5109 (Online)
- Download the Paper 754KB
2.1 Data Sources
We rely on three main data sources for information on new passenger vehicle registrations, house price changes, and other covariates. We describe each data source in turn below.
New passenger vehicle registrations: The ABS Motor Vehicle Census provides an annual snapshot of vehicle registrations in Australia, sourced from each state's motor vehicle registry, disaggregated by postcode of the owner. The dataset reports the number of vehicles in each postcode by year of manufacture, from which we can infer the number of new (or near-new) vehicles registered.[2] Figure 1 shows that, except for NSW, there is a close correspondence between the Motor Vehicle Census data and VFACTS new vehicle sales data, sourced from car dealers.[3] We focus on passenger vehicles to exclude light commercial vehicles and trucks, but we cannot separate private and commercial passenger vehicle registrations. Housing wealth may be a source of finance for some small business vehicle purchases, but otherwise the combination of private and commercial registrations introduces noise into our data. We also exclude a small number of postcodes with more than three times the average level of per capita new passenger vehicle registrations, which are likely to be business-centric postcodes.
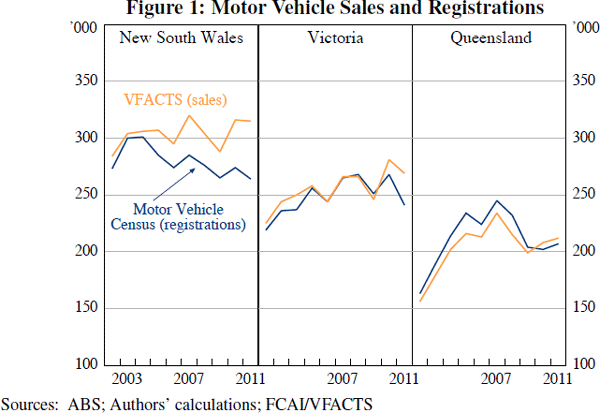
Dwelling prices: We use Australian Property Monitors (APM) unit-record data on property sales for Sydney, Melbourne, and Brisbane to construct annual estimates of the mean price of dwellings in each postcode. At an annual frequency, there are a sufficiently large number of transactions in each postcode to form reliable estimates of mean dwelling prices. We adjust the data to control for quality differences between the housing stock and the properties sold each year. Following Hansen (2009), the following hedonic price adjustment model is fitted to data for each city:
where δijt is a dummy variable equal to unity if property
j
in postcode i is sold in year t, and pijt
is the sale price. The vector of explanatory variables 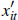 includes controls for
the property type (apartment or house), number of bedrooms, and sale mechanism
(auction or private
treaty).[4]
includes controls for
the property type (apartment or house), number of bedrooms, and sale mechanism
(auction or private
treaty).[4]
Property type is interacted with each explanatory variable, allowing the effect of
housing characteristics on price to differ for apartments and houses. The coefficient
λit is used to construct 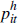 , the hedonically adjusted
average sale price in postcode i in year t, for a property
with the baseline set of
characteristics.[5]
These coefficients are used to calculate year-average growth rates in house
prices. Because the population share of housing characteristics differs at
the postcode level, the estimates
, the hedonically adjusted
average sale price in postcode i in year t, for a property
with the baseline set of
characteristics.[5]
These coefficients are used to calculate year-average growth rates in house
prices. Because the population share of housing characteristics differs at
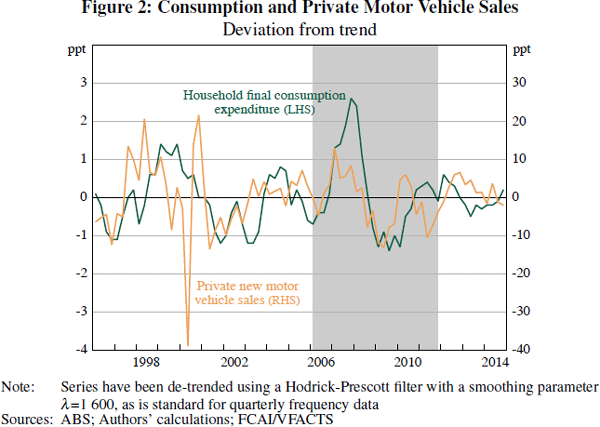
the postcode level, the estimates 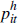 do not correspond to the average postcode-level
house price. See Hansen (2009) and Genesove and Hansen (2014) for further details
on hedonic price adjustment of Australian house price data.
do not correspond to the average postcode-level
house price. See Hansen (2009) and Genesove and Hansen (2014) for further details
on hedonic price adjustment of Australian house price data.
Census of Population and Housing: The Census provides a rich set of control variables at the postcode level: population, income, housing tenure type, usual monthly mortgage repayments, education level, and the unemployment rate. We choose to estimate housing wealth effects over the 2006 to 2011 period, to align with the census years.
Summary statistics are reported in Table 1.
| Mean | Median | Std dev | Percentile | ||
|---|---|---|---|---|---|
| 10th | 90th | ||||
| Average house price, $'000, 2006 | 460.3 | 410.8 | 195.3 | 278.1 | 708.8 |
| Δ average house price, $'000, 2006–11 | 146.3 | 132.8 | 84.6 | 58.0 | 246.5 |
| Percentage change in average house price, 2006–11 | 28.1 | 26.7 | 11.3 | 14.9 | 43.0 |
| Percentage change in average house price, 2001–06 | 37.6 | 35.6 | 13.4 | 23.9 | 57.8 |
| Percentage change in average house price, 1996–01 | 55.8 | 54.7 | 14.0 | 41.9 | 73.4 |
| Per capita new passenger vehicles purchased, 2006 | 0.054 | 0.043 | 0.058 | 0.028 | 0.076 |
| Δ per capita new passenger vehicles purchased, 2006–11 | −0.006 | −0.003 | 0.031 | −0.016 | 0.004 |
| Percentage change in new passenger vehicles purchased, 2006–11 | −8.9 | −7.3 | 25.3 | −29.9 | 9.5 |
| Mean income, $'000 pa, 2006 | 82.5 | 78.1 | 19.5 | 59.1 | 109.2 |
| Δ mean income, $'000 pa, 2006–11 | 7.0 | 7.8 | 5.8 | 0.2 | 13.4 |
| Median income, $'000 pa, 2006 | 74.5 | 67.6 | 22.6 | 46.8 | 96.2 |
| Δ median income, $'000 pa, 2006–11 | 3.7 | 3.9 | 10.4 | −9.1 | 14.3 |
| Unemployment rate, 2006 | 5.3 | 4.6 | 2.4 | 3.0 | 8.6 |
| Δ unemployment rate, 2006–11 | 0.5 | 0.6 | 0.8 | −0.5 | 1.5 |
| Per cent of households who rent, 2006 | 29.3 | 27.2 | 13.3 | 14.5 | 48.3 |
| Per cent of households with a mortgage, 2006 | 31.3 | 29.1 | 10.7 | 20.0 | 47.1 |
| Per cent of households owning outright, 2006 | 39.3 | 39.8 | 9.2 | 26.5 | 51.5 |
| Per cent of people with a bachelor's degree or higher, 2006 | 18.4 | 16.1 | 11.0 | 6.7 | 35.0 |
| Per cent of people with a certificate qualification, 2006 | 7.1 | 7.2 | 1.8 | 4.6 | 9.4 |
| Distance to CBD, km | 19.3 | 17.5 | 12.1 | 5.2 | 38.4 |
| Waterfront dummy | 0.2 | 0.0 | 0.4 | 0.0 | 1.0 |
|
Note: Data are weighted by postcode population in 2006 Sources: ABS; APM |
|||||
2.2 Identification of Housing Wealth Effects
Following Mian et al (2013), our identification approach uses postcode-level variation to estimate the relationship between house prices and consumption (proxied by new vehicle registrations). Ideally, we would like to estimate the causal effect of changes in housing wealth on consumption. This requires house price variation at the postcode level that is uncorrelated with determinants of consumption growth other than housing wealth. A key concern for all studies attempting to identify housing wealth effects is a third factor, such as income growth, that simultaneously affects both consumption and house prices. Failing to control for such third factors would lead us to overestimate the size of the direct effect of house prices on consumption.
Our identification approach has several strengths that help us to identify the direct effect of changes in house prices on consumption. First, the alignment of our estimation period with the Census means we are able to control for a number of third factors that are likely to simultaneously affect both house prices and consumption, such as income growth and the change in the unemployment rate. This contrasts with Mian et al (2013), who do not include the unemployment rate as a control variable in their postcode-level analysis. The larger MPCs that they estimate for low- compared with high-income postcodes could in part be attributable to low-income postcodes being more susceptible to unemployment. Second, there is little serial correlation in relative house price growth at the postcode level. The lack of serial correlation implies that postcode-level relative price changes are highly persistent and largely unpredictable based on lagged relative price growth.[6] This is important, because the permanent income hypothesis predicts that consumption growth is only affected by unanticipated changes in wealth. Third, we include regional fixed effects in our regressions and identify the relationship between house prices and new vehicle registrations using only within-city variation.
The within-city variation in house prices that we exploit is weakly spatially correlated. Table 2 reports the degree of spatial correlation in postcode-level house price growth, based on Moran's I statistic, within each region shown (e.g. Sydney, north). Moran's I statistic is a generalisation of the standard Pearson correlation coefficient, lying between minus one and plus one. A statistic of plus one indicates perfect clustering, minus one indicates perfect dispersion, and zero indicates random assignment. The degree of spatial correlation is statistically significantly different than zero for most cities and regions, but it is economically small.[7]
| I statistic | Standard error | Obs | Population 2006 '000 |
|
|---|---|---|---|---|
| Sydney | 0.133*** | (0.007) | 218 | 2,807 |
| North | 0.144*** | (0.022) | 63 | 707 |
| South | −0.025 | (0.027) | 28 | 471 |
| East | 0.089*** | (0.023) | 53 | 576 |
| West | 0.290*** | (0.019) | 74 | 1,052 |
| Melbourne | 0.077*** | (0.012) | 216 | 2,514 |
| South | 0.034 | (0.032) | 87 | 1,056 |
| East | 0.107*** | (0.016) | 91 | 952 |
| West | 0.043*** | (0.031) | 36 | 489 |
| Brisbane | 0.099*** | (0.011) | 123 | 1,306 |
|
Notes: Moran's I statistic is a measure of spatial correlation: a value of one indicates perfect clustering, a value of minus one indicates perfect dispersion, and a value of zero indicates random assignment; ***, **, and * indicate statistical significance at the 1, 5, and 10 per cent levels, respectively Sources: APM; Authors' calculations |
||||
If households in adjacent postcodes are similar, they should experience common economic shocks, inducing a positive correlation in house price growth across adjacent postcodes. We interpret the absence of strong spatial correlation in house price growth as a sign of plausibly exogenous variation. But to the extent that we have not been able to fully account for third factors causing comovement in house prices and growth in new vehicle registrations, our estimated effects should be interpreted as an upper bound on the direct effect of house prices on consumption.
2.3 Relationship of New Vehicle Registrations to Total Consumption
Our identification scheme relies on new vehicle registrations being a suitable proxy for total consumption. Figure 2 shows the cyclical behaviour of total household consumption and private new motor vehicle sales. (Figure 2 shows aggregate sales data because registrations data are unavailable at a quarterly frequency.) The cyclical component is the deviation of the log of each series from a Hodrick-Prescott filter trend. The timing of new vehicle sales can be particularly affected by temporary factors, such as the introduction of the GST in 1999/2000, but overall there is a strong correlation between new vehicle sales and total consumption. For the 2006 to 2011 sample period used in our analysis, the correlation between the cyclical components of new vehicle sales and total consumption is 0.56. Notably, new vehicle sales is much more cyclically sensitive than total consumption, as indicated by the respective scales for the lines in Figure 2. This is consistent with the finding by Mian et al (2013) that new vehicle sales are much more sensitive to changes in housing wealth than is total consumption.
2.4 Stability of Key Covariates over Time
While we exploit variation in new vehicle registrations and house price growth across postcodes, we also make use of the fact that some covariates are relatively stable through time. In particular, we rely on there being predictable differences across postcodes in the home ownership share and the level of income. On average, about 70 per cent of households own their home either outright or with a mortgage, and the correlation in ownership shares at the postcode level for 2006 and 2011 is 0.98. As expected, there are also highly predictable differences in the level of income through time: the correlation between postcode-level median income in 2006 and 2011 is 0.96. We make use of these predictable differences in income across postcodes when seeking to identify heterogeneity in MPCs by income level.
Footnotes
New vehicles sold until April each calendar year are mostly manufactured in the previous year. This corresponds closely to the 31 March ABS Motor Vehicle Census date used prior to 2011. From 2011, the Census date shifted to 31 January, effectively allowing us to infer only the first ten months of new car sales. Because this measurement change applies equally to all postcodes and our identification uses cross-sectional variation, the effect of this measurement change is absorbed into the constant term in our regressions, and does not affect our results. [2]
Data for other states, not shown, also show a close correspondence. We are not sure why the VFACTS data exceed the Motor Vehicle Census data for NSW. The cross-sectional variation used in our analysis swamps the trend difference evident between the data sources for NSW as a whole. [3]
Thanks to Matthew Read for help with the house price data. [4]
Assuming pijt is log-normally distributed, 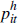 = exp(μ
+ λit
+ var(εijt)/2), where μ
is the baseline set of characteristics.
[5]
= exp(μ
+ λit
+ var(εijt)/2), where μ
is the baseline set of characteristics.
[5]
The correlation between postcode-level house price growth over the periods 1996 to 2001 and 2001 to 2006 is –0.06; the correlation between house price growth over the periods 2001 to 2006 and 2006 to 2011 is 0.13. [6]
Geocoded latitude and longitude coordinates for each postcode are used to calculate pairwise distances between postcodes. For computational feasibility, we use an 11km bandwidth for pairwise comparisons. Brisbane is treated as a single region, because it has about half as many postcodes as Sydney and Melbourne. [7]